Droites parallèles et perpendiculaires : exercices de maths en 6ème corrigés en PDF.
Les droites parallèles et perpendiculaires avec une série d’exercices de maths en 6ème corrigés, vous comprendrez davantage ce chapitre. Par conséquent, cela nécessite une bonne concentration et de la pratique régulière ainsi que l’assimilation des définitions, propriétés et théorèmes du cours. Ainsi, l’élève devra savoir tracer des droites parallèles et perpendiculaires par le biais de son matériel de géométrie (règle, équerre et compas).
Exercice 1 :
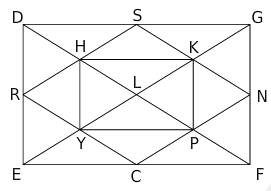
Dans cette figure, les droites qui semblent perpendiculaires ou parallèles, le sont réellement.
- La droite perpendiculaire à (HK) passant par H est la droite …. .
- La droite perpendiculaire à (CE) passant par N est la droite …. .
- La droite parallèle à (HP) passant par N est la droite … .
- La droite parallèle à (CF) passant par S est la droite … .
- La droite parallèle à (PN) passant par R est la droite … .
Exercice 2 :
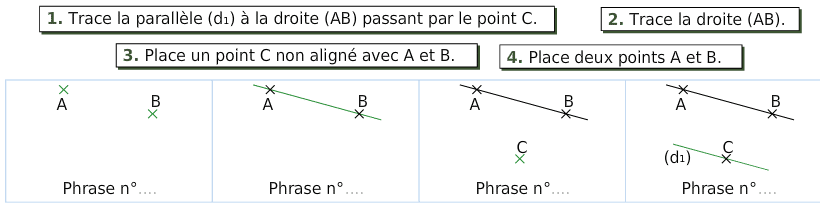
Pour chaque étape de la construction, choisir, parmi les phrases suivantes, celle qui convient.
Exercice 3 :
- a) Placer trois points A, B et C non alignés.
- b) Tracer la droite (AB).
- c) Placer les points D, E et F tels que :
- D
(AB) et D
[AB] ;
- E
(AC) et E
[CA) ;
- F
(BE) et F
(CD).
Exercice 4 :
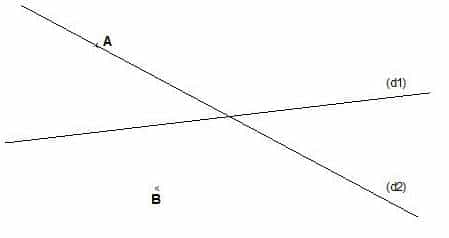
- Tracer la droite (d3) perpendiculaire à la droite (d1) passant par le point A.
- Tracer la droite (d4) perpendiculaire à la droite (d2) passant par le point A.
- Tracer la droite (d5) parallèle à la droite (d1) passant par le point B.
- Tracer la droite (d6) parallèle à la droite (d2) passant par le point B.
Exercice 5 :
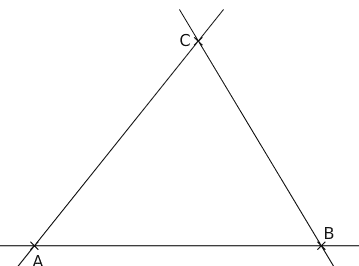
A, B et C sont trois points non alignés.
- Tracer la droite (d1) perpendiculaire à (AB) passant par C.
- Tracer la droite (d2) perpendiculaire à (BC) passant par A.
- Tracer la droite (d3) perpendiculaire à (AC) passant par B.
- Comment sont les droites (d1), (d2) et (d3) ?
Exercice 6 :
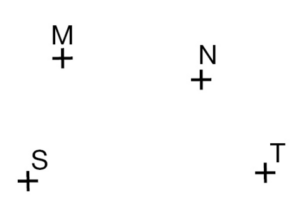
a. Placer quatre points comme ci-dessous.
b. Tracer les segments [MT] et [SN]. Se coupent-ils ?
Si oui, noter P ce point commun.
c. Tracer les droites (MN) et (ST). Se coupent-elles ?
Si oui, noter R ce point commun.
Exercice 7 :
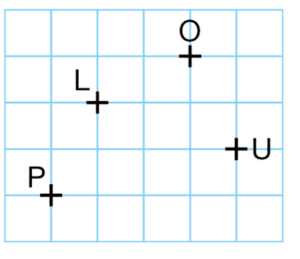
a. Reproduire cette figure.
b. Tracer les segments [LO] et [PU]. Se coupent-ils ?
c. Tracer les demi-droites [PL) et [UO). Se coupent-elles ?
Si oui, noter T ce point commun.
Exercice 8 :
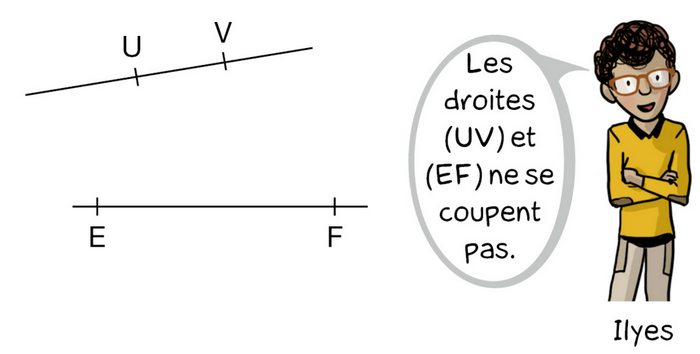
a. Ilyes a-t-il raison ?
b. Tracer cette figure et placer :
- le point C commun aux droites (EU) et (FV) ;
- le point P commun aux droites (UF) et (VE).
Exercice 9 :
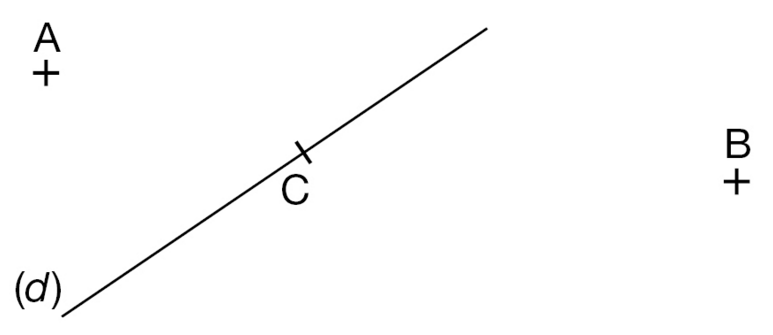
1.Tracer cette figure où (d) est une droite qui passe par le point C.
2. Tracer la perpendiculaire la droite (d) qui passe :
a. par A; b. par B; c. par C.
Exercice 10 :
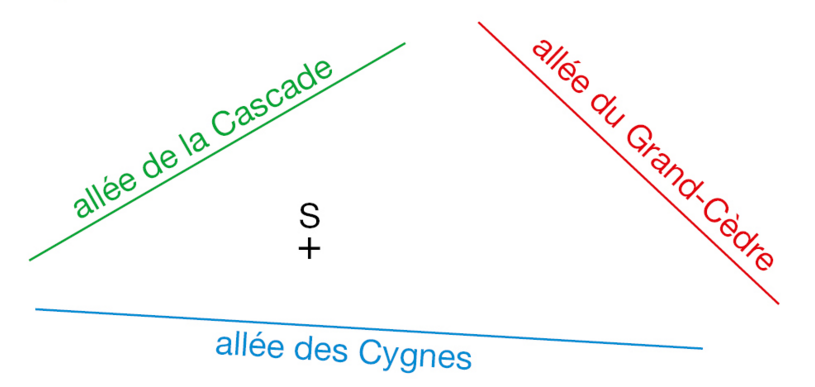
Une statue est représentée par le point S.
On souhaite relier la statue aux trois allées par des passages perpendiculaires à ces allées.
Tracer cette figure et représenter les trois passages.
Exercice 11 :
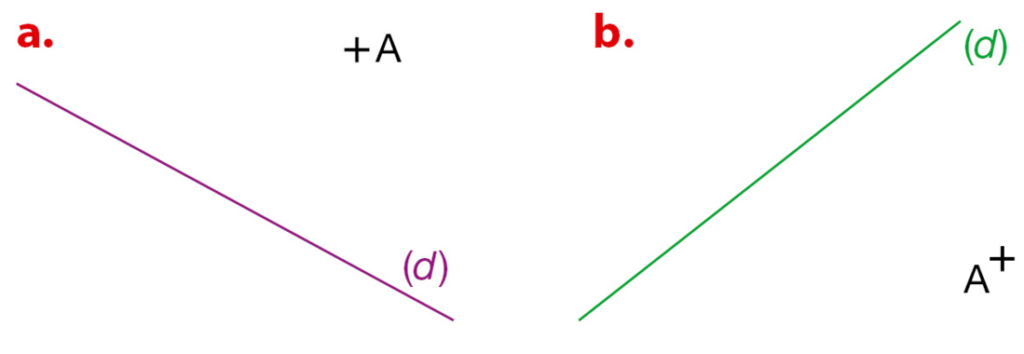
Dans chaque cas, tracer la figure et construire la droite (d’) qui passe par le point A et qui est parallèle à
la droite (d).
Exercice 12 :
1. Placer six points comme ci-dessous.
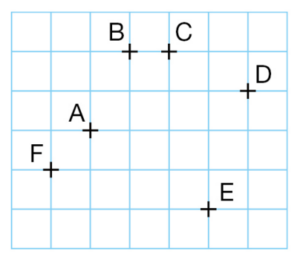
2. Dans chaque cas, écrire avec les notations mathématiques et compléter la
figure.
a. Le segment d’extrémités les points A et B.
b. La droite passant par les points C et D.
c. La demi-droite d’origine B passant par E.
d. Un point I appartenant à la droite qui passe par les points E et F.
Exercice 13 :
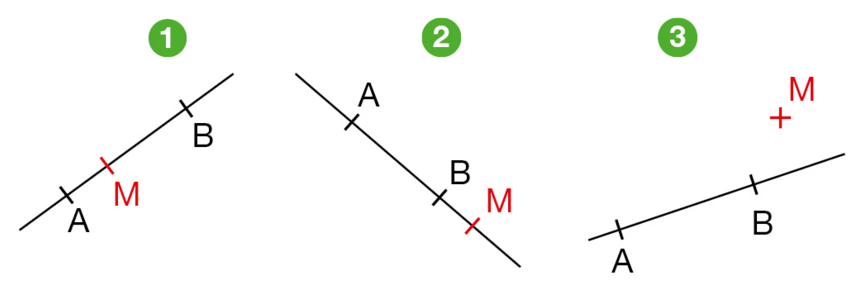
Répondre aux questions pour chaque figure.
a. Compléter les phrases ci-dessous par « appartient » ou « n’appartient pas ».
• Le point M .. à la droite (AB).
• Le point M .. au segment [AB].
b. Traduire ces deux phrases en langage mathématique avec le signe ou
.
Exercice 14 :
Les points A, M, N, P et B sont alignés.
Recopier chaque expression en complétant par ou
, puis lire à voix haute.
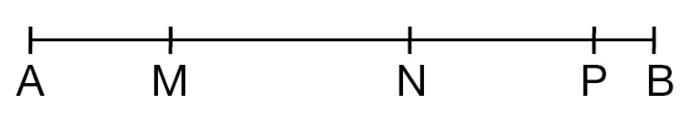
a. M… [AB]
b. P… [MN]
c. B … (AN)
d. N … (BP)
e. M .. [AN]
f. A … [PM]
Exercice 15 :
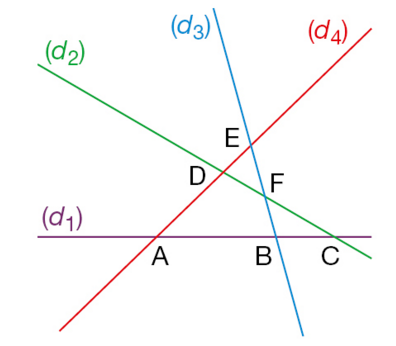
Recopier les phrases et observer la figure pour les compléter.
a. Les droites et
se coupent en … .
b. Le point commun aux droites et
est … .
c. D est le point commun aux droites … et … .
d. Les droites et
…. au point … .
e. A est le point … aux … .
Exercice 16 :
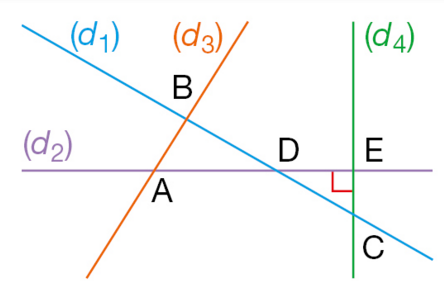
Recopier les phrases en les complétant.
a. Les droites et
sont sécantes en … .
b. Le point d’intersection des droites et
est … .
c. B est … d’intersection des droites … et … .
d. C est le point … des droites … et … .
e. Les droites et
sont …
f. Les droites et
sont … en … .
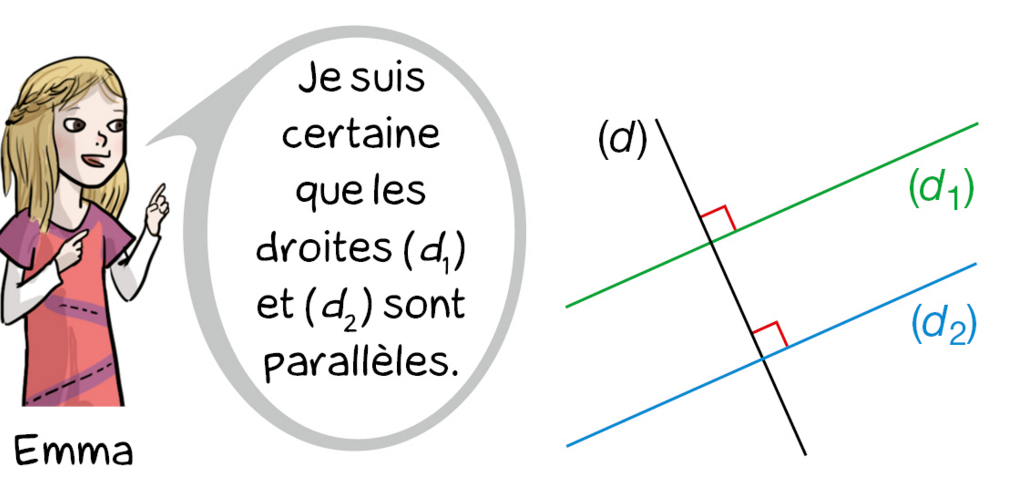
Exercice 17 :
Emma a-t-elle raison ? Justifier votre réponse.
Télécharger puis imprimer cette fiche en PDF.Télécharger ou imprimer cette fiche «droites parallèles et perpendiculaires : exercices de maths en 6ème corrigés en PDF.» au format PDF afin de pouvoir travailler en totale autonomie.
D'autres cours et exercices à consulter
- L’aire et le périmètre : exercices de maths en 6ème corrigés en PDF.
- Proportionnalité : exercices en 6ème de maths corrigés en PDF.
- Symétrie axiale : exercices de maths en 6ème corrigés en PDF.
- Bissectrice d’un angle : exercices de maths en 6ème corrigés en PDF.
- Triangles et quadrilatères : exercices de maths en 6ème corrigés en PDF.
- Cercle : exercices de maths en 6ème corrigés en PDF.
- Fractions : exercices de maths en 6ème corrigés en PDF.
- Nombres décimaux : exercices de maths en 6ème corrigés en PDF.