Droites parallèles et perpendiculaires : cours de maths en 6ème en PDF.
L’élève devra savoir effectuer des construction à l’aide du matériel de géométrie ainsi que maitriser les différentes notations mathématiques sur les droites. Les 3 propriétés essentielles doivent êtres sues afin de pouvoir effectuer des démonstrations en classe de sixième.
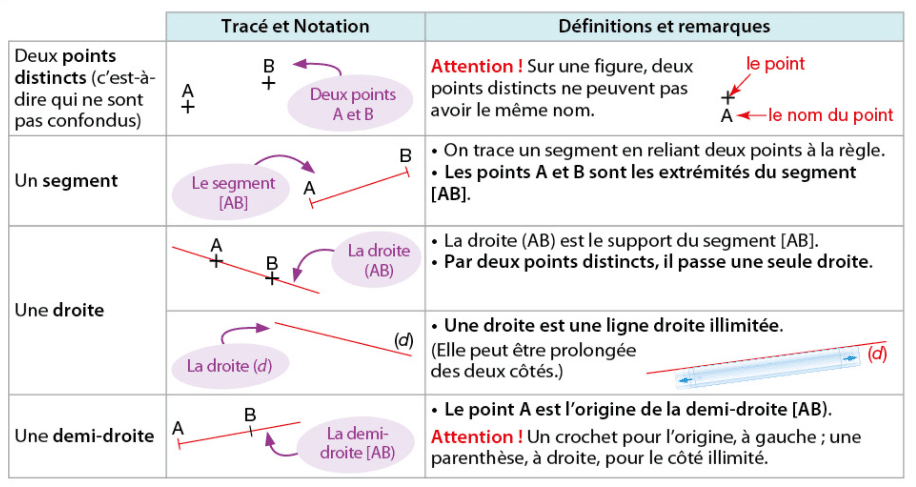
I. Point, segment, droite et demi-droite
1.Vocabulaire, représentations et notations
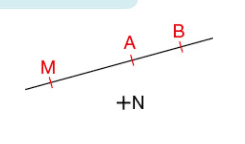
2. Alignement et appartenance
Des points alignés sont des points qui appartiennent à la même droite.
Exemple :
Sur la figure ci-dessous, les points A, B et M sont alignés.
- Le point M appartient à la droite (AB). On note
.
- Le point N n’appartient pas à la droite (AB).On note
.
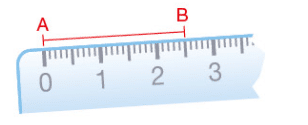
3. Distance entre deux points
La distance entre deux points est la longueur du plus court chemin entre ces deux points. C’est la longueur du segment qui joint ces deux points.
Exemple :
La distance entre les points A et B est de 2,5 cm.
On note : AB = 2,5 cm.
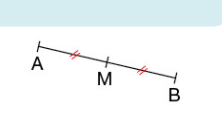
4. Milieu d’un segment
Le milieu d’un segment est le point de ce segment qui le partage en deux segments de même longueur.
Exemple :
Le point M est le milieu du segment [AB].
En effet : les points A, M et B sont alignés et MA=MB.
II. Les droites perpendiculaires
1.Les droites sécantes
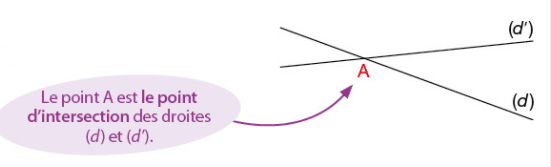
Deux droites sécantes sont deux droites qui ont un seul point en commun.
Exemple :
Les droites (d) et (d’) sont sécantes en A.
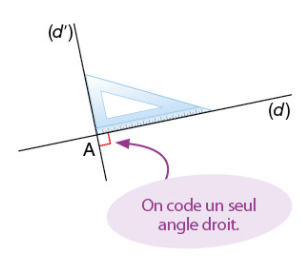
2. Les droites perpendiculaires
Deux droites perpendiculaires sont deux droites sécantes qui forment quatre angles droits.
Exemple et notation :
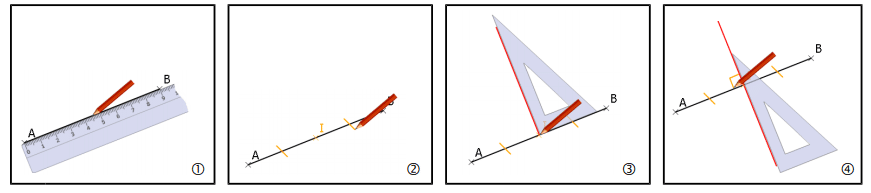
On utilise la règle et l’équerre pour tracer deux droites perpendiculaires.
Les droites (d) et (d’) ci-dessous sont perpendiculaires en A.
On note .
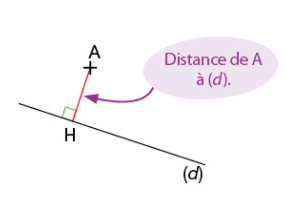
3. Distance d’un point à une droite
La distance d’un point à une droite est la longueur du plus court chemin entre ce point et la droite.
La distance d’un point A à une droite (d) est la distance (AH) entre A et H, pied de la perpendiculaire menée de A à la droite (d).
4. La médiatrice d’un segment
La médiatrice d’un segment est la droite perpendiculaire à ce segment en son milieu.
Exemple :
La droite (d) est la médiatrice du segment [AB].
En effet :
- La droite (d) est perpendiculaire à la droite (AB);
- La droite (d) coupe le segment [AB] en son milieu.
III. Droites parallèles
1.Les droites parallèles
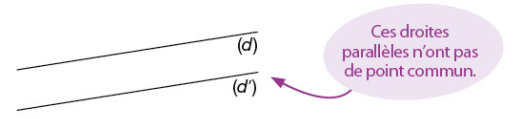
Deux droites parallèles sont deux droites qui ne sont pas sécantes.
Exemple et notation :
Les droites (d) et (d’) sont parallèles.
On note (d)//(d’).
Remarque :
Lorsque les points A, B et C sont alignés, on dit que les droites (AB) et (AC) sont confondues.
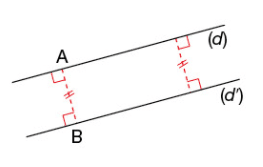
2.Distance entre deux droites parallèles
La distance entre deux droites parallèles est la longueur du plus court chemin entre ces deux droites.
La distance entre deux droites parallèles (d) et (d’) est la longueur d’un segment [AB]perpendiculaire à ces deux droites avec A un point de (d) et B un point de (d’).
3.Deux propriétés
Si deux droites sont perpendiculaires à une même troisième, alors elles sont parallèles.
Si deux droites sont parallèles, et si une troisième droite est perpendiculaire à l’une, alors elle est aussi perpendiculaire à l’autre.
Avez-vous assimilé ce cours sur les droites parallèles et perpendiculaires en 6ème ?
Un QCM de maths sur les droites parallèles et perpendiculaires en 6ème.
Télécharger ou imprimer cette fiche «droites parallèles et perpendiculaires : cours de maths en 6ème en PDF.» au format PDF afin de pouvoir travailler en totale autonomie.
D'autres cours et exercices à consulter
- Quadrilatères : cours de maths en 6ème en PDF.
- Symétrie axiale : cours de maths en 6ème en PDF.
- Proportionnalité et pourcentages : cours de maths en 6ème en PDF.
- Périmètres et aires : cours de maths en 6ème en PDF.
- Pavé droit et volumes : cours de maths en 6ème en PDF.
- Multiplication : cours de maths en 6ème en PDF.
- La médiatrice et la bissectrice : cours de maths en 6ème en PDF.
- Les fractions : cours de maths en 6ème en PDF.