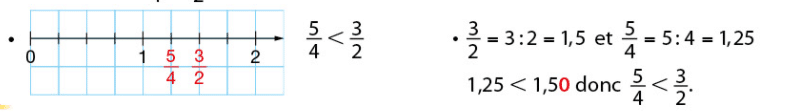Les fractions : cours de maths en 6ème à télécharger en PDF.

Mis à jour le 29 mars 2025

Sommaire de cette fiche

Les fractions avec un cours de maths en 6ème à imprimer ou à télécharger gratuitement en PDF.
Ainsi que les quotients et les égalités. L’élève devra maitriser la définition et savoir placer son abscisse sur une droite graduée ainsi que d’effectuer des calculs de produits d’un nombre par un quotient ou de calculer des proportions. Les fractions sont une notion primordiale, essentiellement, sur la comparaison de deux nombres qui ne seraient pas des nombres décimaux. La résolution de problèmes sera également un élément central sur ce chapitre en classe de sixième.
De nombreuses compétences seront développer comme savoir représenter graphiquement la fraction d’une figure ou d’une quantité ou encore de savoir comparer deux quotients ou de les ranger dans le sens croissant ou décroissant.

I. Fractions et quotients

1.Définition et vocabulaire

Définition :

Quand on partage une unité en parts égales, chaque part est une fraction de l’unité.

Exemple :

Ce rectangle représente l’unité; on le partage en quatre parts égales.

Chaque partie représente la fraction $Fractions$ .

$Fractions$ , c’est à dire $4\times \frac{1}{4}=1$ .

$fractions$

2. Placement et comparaison sur une demi-droite graduée

Exemple :

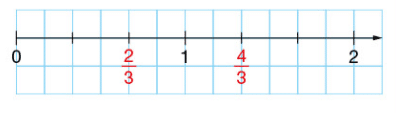
Pour placer le nombre $\frac{7}{3}$ sur une demi-droite graduée, on reporte sept fois le tiers de l’unité

$( \frac{7}{3}=7\times \frac{1}{3} )$ ou bien on utilise $Fractions$ .

3. Quotient

$quotient et fractions$

II. Propriétés des fractions

1.Egalités de fractions simples

Exemple 1 :

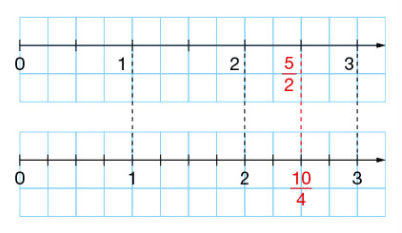
On a placé le nombre $\frac{5}{2}$ sur cette demi-droite graduée.

On partage l’unité en deux fois plus de parts; on prend alors deux fois plus de parts

et donc $Fractions$ .

$Egalites de fractions$

Exemple 2 :

Voici différentes fractions égales à $\frac{2}{3}$ .

$Proportions et fractions$

2.Comparaison et demi-droite graduée

Propriété :

Pour comparer deux fractions, on peut s’aider d’une demi-droite graduée ou utiliser leur écriture décimale (quand elle existe).

Exemple 1 :

Sur cette demi-droite graduée, $\frac{2}{3}$ est plus proche de 0 que de $Fractions$ donc $\frac{2}{3}<\frac{4}{3}$ .

Exemple 2 :

Pour comparer $\frac{5}{4}$ et $\frac{3}{2}$ , on peut procéder de l’une des façons suivantes :

$comparer des fractions$

3.Prendre une fraction d’une quantité

Propriété :

Prendre une fraction d’une quantité, c’est multiplier cette fraction par cette quantité.

Exemples :

Prendre $\frac{1}{3}$ de 15 L, c’est calculer $\frac{1}{3}\times 15=\frac{15}{3}=15:3=5\,L$ .
Prendre $\frac{2}{3}$ de 15 L, c’est calculer 2 fois $\frac{1}{3}$ de 15 L , soit $\frac{2}{3}\times 15=2\times ( 15:3 )=2\times 5=10\,L$ .

Avez-vous assimilé ce cours sur les fractions ?

Les fractions

QCM sur les fractions en 6ème.

Télécharger puis imprimer cette fiche en PDF.

Télécharger ou imprimer cette fiche «les fractions : cours de maths en 6ème en PDF.» au format PDF afin de pouvoir travailler en totale autonomie.