Fraction, puissance, racine carrée : exercices de maths en 2de.

Les fractions, les puissances, les racines carrées et les intervalles avec une série d’exercices de maths en 2de corrigés. Vous allez bénéficier d’une compréhension approfondie de ce chapitre. En effet, ces énoncés font intervenir les notions suivantes :

calculs avec les fractions, puissances;
calculs avec les racines carrées;
résoudre des équations;
résoudre des inéquations;
union et intersection d’intervalles;

Exercice 1 :

Mettre les nombres suivants sous forme irréductible , en détaillant les calculs

$a=\frac{1+\frac{2}{5}}{3-\frac{7}{5}}$

$b=\frac{3^7\times \,(2^{-3})^5\times 6^4}{(3^2)^5\times (2^{-5})^2}$

$c=\frac{10^4\times 15^2}{(2^3)^2\times 12^3}$

Exercice 2 :

Mettre les nombres suivants sous forme scientifique

$a=\frac{13}{25}\times 10^9$

$b=\frac{4,195}{0,125}\times 10^{-5}$

Exercice 3 :

Calculez et simplifiez $a=\frac{\sqrt{81}}{\sqrt{242}}\times \sqrt{\frac{98}{25}}$

Exercice 4 :

Au a) résoudre dans $\mathbb{R}$ l’équation d’inconnue x . Rédiger soigneusement votre résolution.

Dans le b) exprimer y en fonction de x et préciser la valeur interdite pour x :

a) $3(2\,-\,5x)\,+\,3\,+\,x\,-\,(1-\,2x)\,=\,5x\,+\,9$ .

b) $2x(3\,-5y)\,+\,5y=\,3x\,-\,2.$

Exercice 5 :

1. Donner l’intervalle représentant l’ensemble des réels x satisfaisant à la condition indiquée

a) $-1\leq\,\,x\,\leq\,\,5$ b) $3<x\,\leq\,\,7$

c) $x\,\geq\,\,3$ d) $x\,\leq\,\,-5$

2. Pour les deux cas suivants, représenter sur une droite graduée les intervalles I et J et donner leur intersection et leur réunion.

a) I = ]-∞ ; 4[ ; J = [1 ; 7]

$I\,\cup\,J\,=\,?$ $I\,\cap\,J\,=\,?$

b) I = ]-7 ; -3] ; J = ]-4 ; +∞[

$I\,\cup\,J\,=\,?$ $I\,\cap\,J\,=\,?$

Exercice 6 :

Effectuer les calculs suivants en respectant les priorités opératoires.

$A=\frac{1}{5}\times \,\frac{-4}{3}+\frac{7}{2}$ $B=\frac{13}{7}+(-\frac{8}{7}):(-\frac{4}{5})$

$C=(\frac{3}{2}+\frac{3}{5})(\frac{5}{4}-\frac{4}{3})$ $D=-\frac{3}{8}-\frac{5}{8}\times \,\frac{7}{9}$

Exercice 7 :

Calculer puis simplifier au maximum le résultat.

$A=\frac{\frac{3}{2}-\frac{1}{3}}{\frac{3}{4}+\frac{2}{3}}$ $B=2+\frac{\frac{2}{7}}{\frac{5}{14}}$ $C=-\frac{3}{14}-\frac{3}{\frac{7}{5}}+2$

$D=\frac{7}{5}+\frac{\frac{8}{15}}{\frac{2}{3}}-\frac{19}{2}$ $E=\frac{3-\frac{7}{5}}{1-\frac{9}{10}}$ $F=\frac{7}{-8}+\frac{6}{4}-1$

Exercice 8 :

Ecrire sous la forme $a\sqrt{b}$ , où et sont deux entiers relatifs, avec b le plus petit possible.

$A=\sqrt{50}+4\sqrt{18}-7\sqrt{8}$

$B=\sqrt{20}-8\sqrt{45}+2\sqrt{5}$

$C=\sqrt{12}+\sqrt{75}+4\sqrt{300}$

$D=5\sqrt{63}-\sqrt{28}+\sqrt{7}$

Exercice 9 :

Développer et simplifier les expressions suivantes.

$A=\frac{\sqrt{2}}{2}(\sqrt{2}+\frac{1}{\sqrt{2}})$ $B=\sqrt{18}(\sqrt{2}-\frac{\sqrt{18}}{18})$

$C=\sqrt{3}(2-5\sqrt{3})$ $D=5\sqrt{2}(\sqrt{2}-7\sqrt{18})$

$E=(\sqrt{6}+2)\sqrt{2}$ $F=2\sqrt{12}(\sqrt{12}-\sqrt{3}+\sqrt{6})$

Exercice 10 :

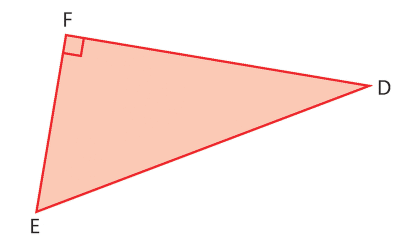
EDF est un triangle rectangle en F.

On donne $ED=5\sqrt{2}$ cm et $DF=3\sqrt{2}$ cm.

1.Déterminer la valeur exacte de EF.

Donner le résultat sous la forme $a\sqrt{2}$ où est un entier positif.

2. Donner la valeur exacte du périmètre du triangle EDF, puis l’arrondi au millimètre.

Exercice 11 :

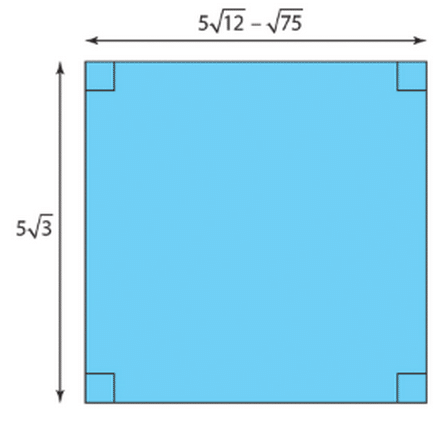
On considère la figure suivante. L’unité est le centimètre.

1.Ecrire $5\sqrt{12}-\sqrt{75}$ sous la forme $a\sqrt{b}$ , où et sont des entiers relatifs, étant le plus petit possible.

2. Quelle est la nature exacte de ABCD ? Justifier

3. Déterminer le périmètre de ABCD sous la forme la plus simple possible.

Donner ensuite l’arrondi au millimètre.

4. Déterminer la valeur exacte de l’aire de ABCD.

Exercice 12 :

L’escalier d’une tour a un nombre de marches compris entre 130 et 150.

Si je les monte trois par trois, j’arrive en haut.

Si j’étais capable de les monter 4 par 4, je finirais par 1 marche.

Combien y a-t-il de marches ?

Exercice 13 :

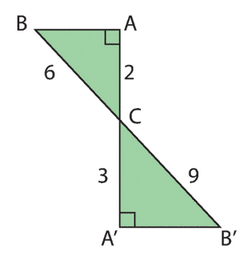
1. Calculer la valeur de $\frac{AB}{A'B'}$ .
2. En utilisant la définition d’une racine carrée, écrire le résultat

précédent sous la forme $\sqrt{\frac{a}{b}}$ où a et b sont des entiers positifs, avec $b\neq\,0$ .
3. Calculer AB puis AB’.
4. Comparer les deux écritures de $\frac{AB}{A'B'}$ et trouver un moyen pour simplifier $\frac{\sqrt{32}}{\sqrt{72}}$ .

$Théorème de Thalès, fractions et racines carrées$

Exercice 14 :

Simplifier les écritures des nombres.

$A=\,(\,\sqrt{3\sqrt{3}}\,\,)^4$

$B=\,(\sqrt{\,\frac{2}{\sqrt{7}}}\,\,)^4$

$C=\frac{5}{\sqrt{5}}\times \,\,(\,\frac{2}{\sqrt{5}}\,\,)^3$

$D=\sqrt{\frac{4}{25}}+\sqrt{\frac{36}{25}}$

$E=\sqrt{\frac{1}{100}}+\sqrt{\frac{49}{25}}$

$F=\,\sqrt{\frac{\frac{9}{8}}{2}\,}+\sqrt{\frac{1}{\frac{1}{81}}}$

Exercice 15 :

a. Démontrer que pour tout entier naturel n non nul :
$\frac{1}{n}-\frac{1}{n+1}=\frac{1}{n(n+1)}$

b. En déduire la valeur de la somme S définie par :
$S=\frac{1}{1\times \,2}+\frac{1}{2\times \,3}+\frac{1}{3\times \,4}+...+\frac{1}{2\,020\times \,2\,021}$

Voir Exercices 11 à 15...

Télécharger puis imprimer cette fiche en PDF.

Télécharger ou imprimer cette fiche «les fractions, puissances et racines carrées : exercices de maths en 2de corrigés en PDF.» au format PDF afin de pouvoir travailler en totale autonomie.

Vous devez vous inscrire ou vous connecter à votre compte afin de pouvoir télécharger ce document au format PDF.

Réviser les cours et exercices avec nos Q.C.M :

Q.C.M en 6ème Q.C.M en 5ème Q.C.M en 4ème Q.C.M en 3ème Q.C.M en 2de Q.C.M en 1ère Q.C.M en Terminale

D'autres ressources pour progresser en autonomie :

Chronomètre Horloge France Tables Multiplication Arrondir des décimaux Rapporteur et Angles Médiatrice Symétrie Axiale d'un triangle Symétrie Centrale d'un triangle Translation d'un triangle Rotation Homothétie Bissectrice Tracer droite parallèle Conversion Aires et Volumes Addition de deux relatifs Soustraction Relatifs Addition et soustraction de trois relatifs Produit Deux Relatifs Produit Trois Relatifs Quotient Relatifs Carré Entier Racine Carrée Théorème Pythagore Liste Diviseurs Décomposition Facteurs Premiers Calcul du PGCD PGCD Algorithme Euclide Test Nombre Premier Déterminer Fonction Linéaire Déterminer Fonction Affine Traceur Courbe Trigonométrie Angle Trigonométrie Longueur Périmètre d'un Cercle Aire d'un Disque Volume du Parallélépipède Rectangle Volume du cylindre Surface d'une Sphère et Volume d'une boule Volume d'une pyramide à base rectangulaire Section d'une pyramide Visualiser Section Cône en 2D Section d'un Cône Carte Mondiale Coordonnées Géographiques

Mathématiques Web c'est 2 250 277 fiches de cours et d'exercices téléchargées.