L’élève devra savoir construire l’image d’une figure par la symétrie axiale d’axe (d) à l’aide du matériel de géométrie. Il devra, également, connaître toutes les propriétés de conservation de la symétrie centrale concernant les longueurs des segments, de l’alignement, de la mesure d’un angle ou encore du périmètre ou de l’aire d’une figure. L’assimilation des différentes propriétés de la symétrie centrale sont essentielles afin de pourvoir effectuer des démonstrations en géométrie en classe de sixième.
I. La symétrie axiale
1.Figures symétriques
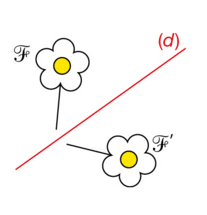
Deux figures sont symétriques par rapport à une droite (d) lorsqu’elles se superposent par pliage autour de la droite (d).
Exemple :
les figures et
ci-dessous sont symétriques par rapport à la droite (d) .
On dit aussi que :
est la symétrique de
par rapport à la droite (d).
est la symétrique de
.
La symétrie axiale par rapport à une droite conserve :
- les longueurs;
- l’alignement;
- les mesures d’angles;
- les aires.
Exemple :
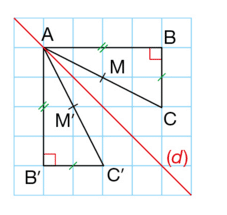
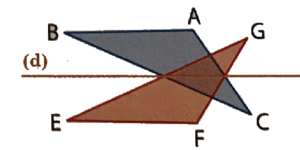
Les triangles rectangles ABC et AB’C’ ci-dessous sont symétriques par rapport à la droite (d).
- AB=A’B’, AC=A’C’, BC=B’C’.
- Le point M est aligné avec les points A et C.
Son symétrique M’ est aussi aligné avec les points A et C’.
et
.
- Les triangles ABC et A’B’C’ ont la même aire.
2.Axe de symétrie d’une figure
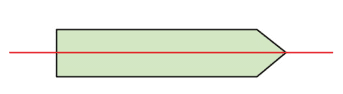
Une droite est un axe de symétrie d’une figure lorsque cette figure coïncide avec sa symétrie par rapport à cette droite.
Exemple :
La droite rouge est l’axe de symétrie de cette figure.
La symétrie par rapport à une droite est aussi appelée symétrie axiale.
3.Symétrie d’un point
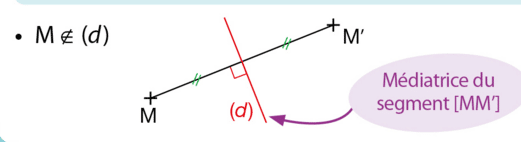
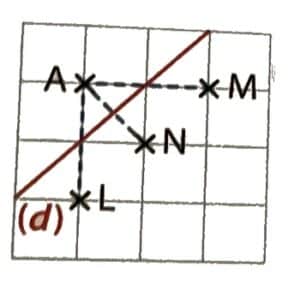
M n’appartient pas à (d).
Le symétrique du point M par rapport à la droite (d) est le point M’ tel que la droite (d) soit la médiatrice du segment [MM’].
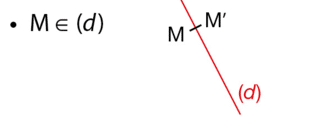
M appartient à (d).
Le symétrique du point M par rapport à la droite (d) est le point M lui-même.
II.Symétrique d’une droite et d’un segment
1.Symétrique d’une droite
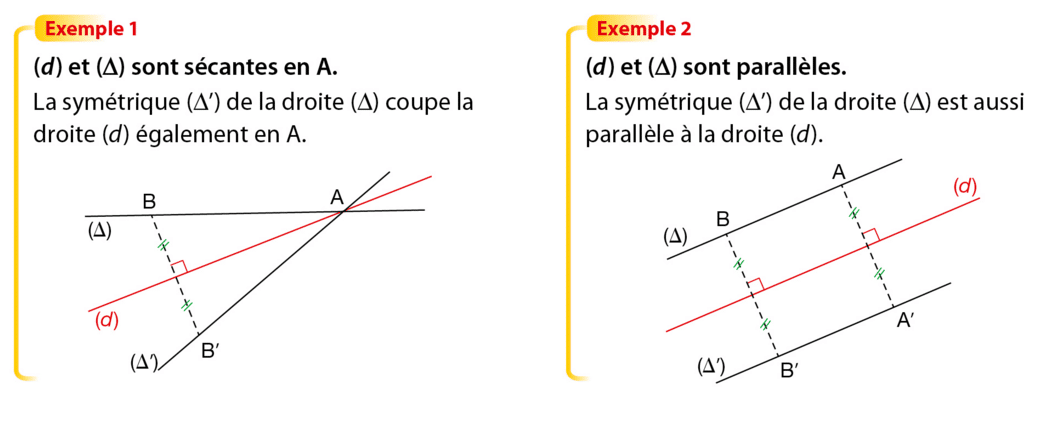
La symétrique d’une droite par rapport à une droite est une droite.
2.Symétrique d’un segment
Le symétrique d’un segment par rapport à une droite (d) est un segment ayant la même longueur.
Le symétrique d’un polygone par rapport à une droite est un polygone qui a le même nombre de côtés.
Exemple :
- Le symétrique par rapport à une droite d’un triangle est un triangle.
- Le symétrique par rapport à une droite d’un carré est un carré.
Avez-vous assimilé ce cours sur la symétrie axiale en 6ème ?
QCM sur la symétrie axiale en 6ème.
Télécharger ou imprimer cette fiche «symétrie axiale : cours de maths en 6ème en PDF.» au format PDF afin de pouvoir travailler en totale autonomie.
D'autres cours et exercices à consulter
- Quadrilatères : cours de maths en 6ème en PDF.
- Proportionnalité et pourcentages : cours de maths en 6ème en PDF.
- Périmètres et aires : cours de maths en 6ème en PDF.
- Pavé droit et volumes : cours de maths en 6ème en PDF.
- Multiplication : cours de maths en 6ème en PDF.
- La médiatrice et la bissectrice : cours de maths en 6ème en PDF.
- Les fractions : cours de maths en 6ème en PDF.
- Droites parallèles et perpendiculaires : cours de maths en 6ème en PDF.