Pavé droit et volumes : cours de maths en 6ème

Pavé droit et volumes : cours de maths en 6ème en PDF.

par
   Le pavé droit et le calcul de volume à travers un cours de maths en 6ème. Dans cette leçon, nous développerons la définition et les unités de volume. Des compétences en géométrie dans l’espace, l’élève devra être capable de tracer en trois dimensions mais également d’utiliser la perspective cavalière afin de le représenter par le biais d’un schéma. La construction du patron et d’autres solides sera demandé ainsi que la maitrise de la formule pour calculer le volume d’un parallélépipède rectangle en géométrie en classe de sixième. Des conversions sur les volumes à maitriser afin de développer ses compétences en calcul.

I. Volume d’un pavé droit

1.Unités de volume

Définition :

Une unité de volume souvent utilisée est le mètre cube ,(\,m^3\,\,).1 m^3 est le volume est le volume d’un cube d’arête 1 m.

On utilise aussi d’autres unités de volume, en particulier :

  • le décimètre cube \,(\,dm^3\,\,) est le volume d’un cube de 1 dm d’arête;
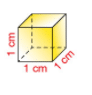
  • le centimètre cube \,(\,cm^3\,\,) est le volume d’un cube de 1 cm d’arête;
  • le millimètre cube \,(\,mm^3\,\,) est le volume d’un cube de 1 mm d’arête;

2.Volume du parallélépipède rectangle par dénombrement

Exemple :

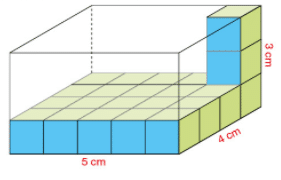
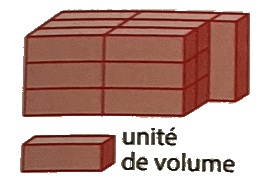
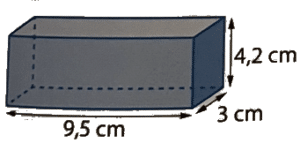
On remplit entièrement le parallélépipède rectangle ci-dessous de cubes de 1 cm d’arête.

Au fond du pavé, on dispose 5 rangées de 4 petits cubes.

5×4=20, il y a donc 20 petits cubes au fond du pavé droit.

Dans le pavé droit, 3 de ces couches sont superposées.

3×20=60, donc le pavé contient 60 cubes d’arête 1 cm.

Le volume de ce parallélépipède rectangle  est donc 60 cm^3.

pavé droit

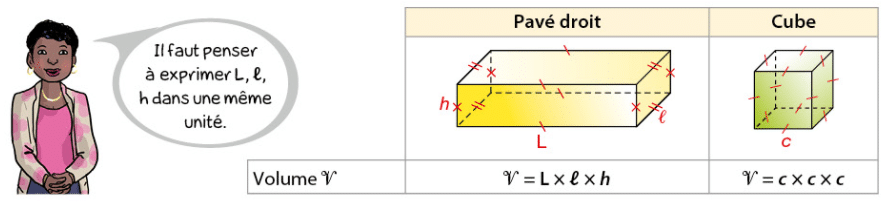
3.Volume et formule

formule du volume d'un pavé droit

Exemple :

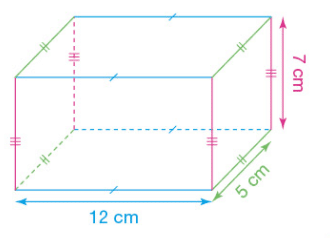
Un parallélépipède rectangle a pour longueur 12 cm, pour largeur 5 cm et pour hauteur 7 cm.

Le volume de ce parallélépipède rectangle est :

V=12\times \,5\times \,7=420\,cm^3

pavé droit

Avez-vous assimilé ce cours sur le pavé droit et le calcul de volumes en 6ème ?

Le pavé droit et calcul de volumes

QCM de maths sur le pavé droit et calcul de volumes en 6ème.

Télécharger puis imprimer cette fiche en PDF.

Télécharger ou imprimer cette fiche «pavé droit et volumes : cours de maths en 6ème en PDF.» au format PDF afin de pouvoir travailler en totale autonomie.

Réviser les cours et exercices avec nos Q.C.M :

Q.C.M en 6ème Q.C.M en 5ème Q.C.M en 4ème Q.C.M en 3ème Q.C.M en 2de Q.C.M en 1ère Q.C.M en Terminale

D'autres ressources pour progresser en autonomie :

Chronomètre Horloge France Tables Multiplication Arrondir des décimaux Rapporteur et Angles Médiatrice Symétrie Axiale d'un triangle Symétrie Centrale d'un triangle Translation d'un triangle Rotation Homothétie Bissectrice Tracer droite parallèle Conversion Aires et Volumes Addition de deux relatifs Soustraction Relatifs Addition et soustraction de trois relatifs Produit Deux Relatifs Produit Trois Relatifs Quotient Relatifs Carré Entier Racine Carrée Théorème Pythagore Liste Diviseurs Décomposition Facteurs Premiers Calcul du PGCD PGCD Algorithme Euclide Test Nombre Premier Déterminer Fonction Linéaire Déterminer Fonction Affine Traceur Courbe Trigonométrie Angle Trigonométrie Longueur Périmètre d'un Cercle Aire d'un Disque Volume du Parallélépipède Rectangle Volume du cylindre Surface d'une Sphère et Volume d'une boule Volume d'une pyramide à base rectangulaire Section d'une pyramide Visualiser Section Cône en 2D Section d'un Cône Carte Mondiale Coordonnées Géographiques

Inscription gratuite à Mathématiques Web.  Mathématiques Web c'est 2 250 077 fiches de cours et d'exercices téléchargées.

✕
Mathématiques Web

GRATUIT
VOIR