Les aires et périmètres de figures géométriques avec des exercices de maths en 6ème corrigés. Vous trouverez dans ces différents exercices une application des différentes formules à connaître par coeur en classe de sixième. Egalement des conversion de longueurs et d’aires. Le périmètre d’une figure géométrique est la longueur de sa circonférence. L’élève devra savoir convertir des grandeurs sur des figures usuelles (carré, rectangle, losange). Des exercices afin de progresser en maths et développer des compétences sur des supports similaires à votre livre scolaire (Hachette, Hatier, Sésamaths, Bordas). Ces énoncés sont corrigés et permettent aux élèves de s’exercer en ligne puis de repérer leurs erreurs afin de combler leurs lacunes et d’envisager une progression sur le chapitre des aires et des périmètres de figures.
Exercice 1 :
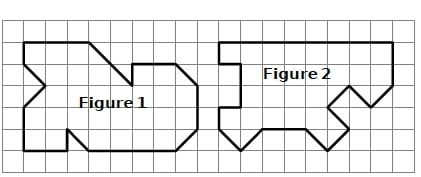
Parmi les figures 1 et 2,
1. Quelle est celle qui a le plus grand périmètre ? Justifie.
2. Quelle est celle qui a la plus grande aire ?Justifie.
Exercice 2 :
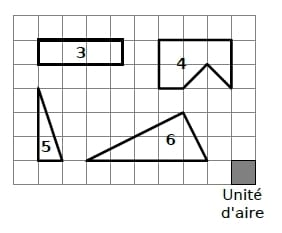
Donne, en unités d’aire, les aires des figures 3 à 6.
Exercice 3 :
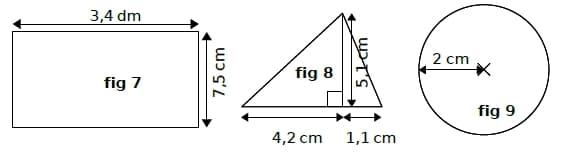
- En détaillant tes calculs, donne en cm les périmètres des figures 7 et 9. Pour la figure 9, tu donneras une valeur approchée au dixième.
- En détaillant tes calculs, donne en cm² les aires des figures 7,8 et 9. Pour la figure 9, tu donneras une valeur approchée au centième.
Exercice 4 :
- Un rectangle a pour longueur 7 cm et pour aire 8,4 cm². Quelle est sa largeur ?
- BUT est un triangle rectangle en U tel que BU = 3,4 cm et UT = 5,3 cm. Quelle est son aire en
cm² ? - Une salle de classe a la forme d’un carré de côté 6,2 m. Quelle est son aire en dam² ? En dm² ?
Exercice 5 :
1. Sur ta copie, trace un triangle d’aire 12 cm².
2. Sur ta copie, trace un rectangle d’aire 18 cm² et de périmètre 38 cm.
Exercice 6 :
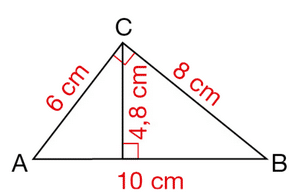
ABC est un triangle rectangle en C.
a. Quel calcul permet C d’obtenir le périmètre du triangle ABC ?
b. Proposer deux méthodes différentes pour calculer l’aire du triangle ABC.
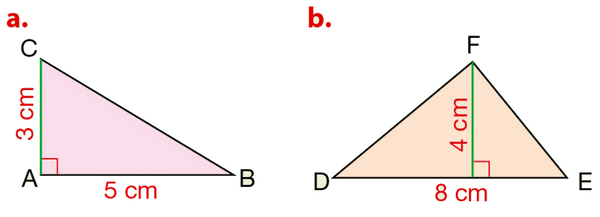
Exercice 7 :
Calculer mentalement l’aire de chaque triangle représenté.
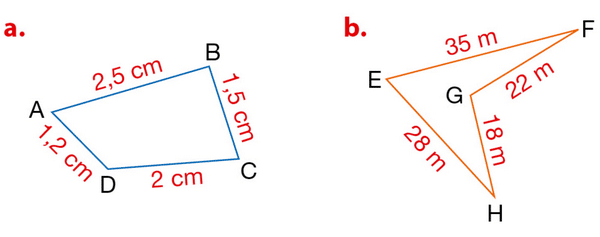
Exercice 8 :
Calculer le périmètre de chaque polygone représenté.
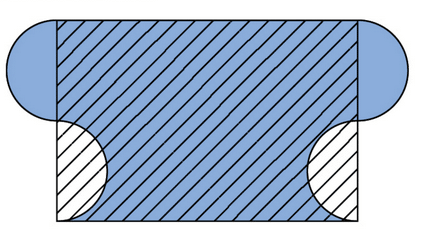
Exercice 9 :
a. Comparer le périmètre du domaine coloré en bleu à celui du domaine hachuré.
b. Comparer l’aire du domaine coloré en bleu à celle du domaine hachuré.
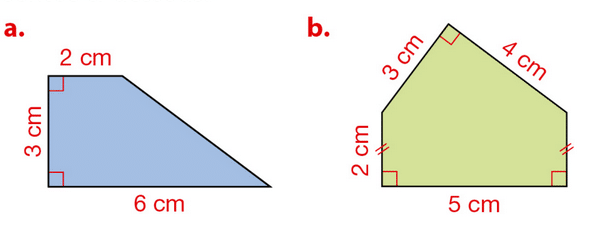
Exercice 10 :
Calculer l’aire de chaque surface colorée représentée ci-dessous.
Exercice 11 :
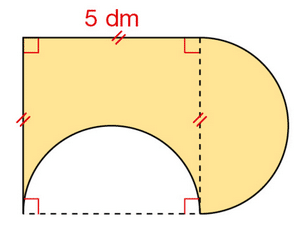
Calculer l’aire, en dm², de la surface colorée représentée ci-dessous
Exercice 12 :
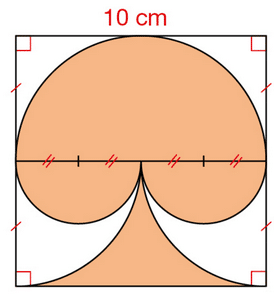
Calculer une valeur approchée au centième près de l’aire, en cm², de ce «champignon » inscrit
dans un carré.
Télécharger ou imprimer cette fiche «l’aire et le périmètre : exercices de maths en 6ème corrigés en PDF.» au format PDF afin de pouvoir travailler en totale autonomie.
Nos applications