Mis à jour le 30 mars 2025

Quadrilatères : cours de maths en 6ème

Quadrilatères : cours de maths en 6ème en PDF.

   Les quadrilatères à travers un cours de maths en 6ème, nous étudierons la définition puis le carré, le rectangle, le losange, le parallélogramme. L’élève devra connaître la définition d’un quadrilatère et savoir le construire à l’aide du matériel de géométrie (règle, compas, équerre et rapporteur). Il devra maitriser les différents quadrilatères particuliers comme le carré, le rectangle, le losange ou encore le cerf-volant. Maitriser les définitions des diagonales, des côtés consécutifs d’un quadrilatère et des côtés opposés en classe de sixième.

I. Les quadrilatères

1.Le vocabulaire des quadrilatères

Définition :

Un quadrilatère est un polygone à quatre côtés.

Vocabulaire :

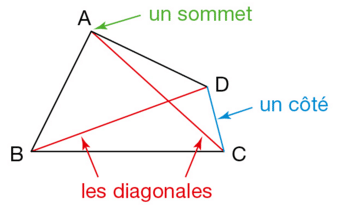
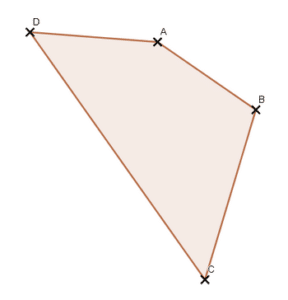
Pour ce quadrilatère ABCD :

  • deux côtés qui n’ont pas de sommet en commun sont dits opposés.
  • deux côtés qui ont un sommet en commun sont dit consécutifs.

Codage d’un quadrilatère :

Règle :

Pour nommer un quadrilatère, on note les sommets dans l’ordre où on les rencontre en tournant dans un certain sens. Ainsi, le quadrilatère ci-dessous peut se noter ABCD, ADCB,  ou BCDA.

quadrilatère

2.Les quadrilatères particuliers

Définition :

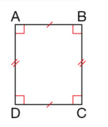
Un rectangle est un quadrilatère qui a quatre angles droits.

Exemple :

ABCD est  un rectangle.

Ses côtés opposés sont parallèles et de même longueur.

rectangle

Définition :

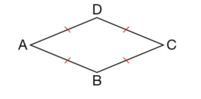
Un losange est un quadrilatère qui a quatre côtés de même longueur.

Exemple :

ABCD est un losange.

losange

Définition :

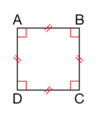
Un carré est un quadrilatère qui a quatre angles droits et quatre côtés de même longueur.Un carré est à la fois un losange et un rectangle.

Exemple :

Le quadrilatère ABCD est un carré. Ses quatre angles sont droits.

Ses quatre côtés ont la même longueur : AB=BC=CD=DA.

carré

Définition :

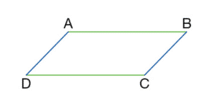
Un parallélogramme est un quadrilatère qui a ses côtés opposés parallèles.

Exemple :

Le quadrilatère ABCD est un parallélogramme.

Ses côtés opposés sont parallèles : (AB)//(DC) et (AD)//(BC).

parallélogramme

Conséquences :

Le carré, rectangle et le losange sont des parallélogramme particuliers.

Avez-vous assimilé ce cours sur les quadrilatères en 6ème ?

Les quadrilatères

Un QCM sur les quadrilatères en 6ème.

4.2/5 - (14 votes)
Télécharger puis imprimer cette fiche en PDF.

Télécharger ou imprimer cette fiche «quadrilatères : cours de maths en 6ème en PDF.» au format PDF afin de pouvoir travailler en totale autonomie.

Vous devez vous inscrire ou vous connecter à votre compte afin de pouvoir télécharger ce document au format PDF.

D'autres cours et exercices à consulter

Inscription gratuite à Mathématiques Web.  Mathématiques Web c'est 2 268 671 fiches de cours et d'exercices téléchargées.