Fonctions affines : exercices de maths en 3ème corrigés en PDF.

Les fonctions affines avec des exercices de maths en 3ème corrigés afin de vous exercer sur des énoncés différents l’un de l’autre.

Vous retrouverez dans cette série les notions suivantes :

définition d’une fonction affine;
coefficient directeur d’une droite et fonction affine;
courbe représentative d’une fonction affine;
calcul d’images et d’antécédent avec une fonction affine;
détermination du coefficient directeur et de l’ordonnée à l’origine;
sens de variation d’une fonction affine.

Ces énoncés corrigés ont été rédigé par un enseignant et sont à consulter en ligne ou à télécharger au format PDF.

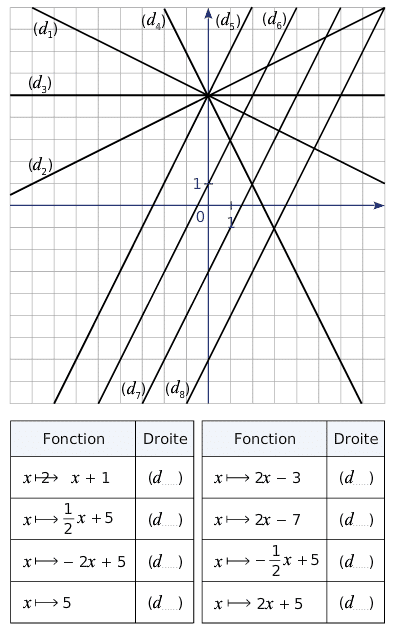
Exercice 1 :

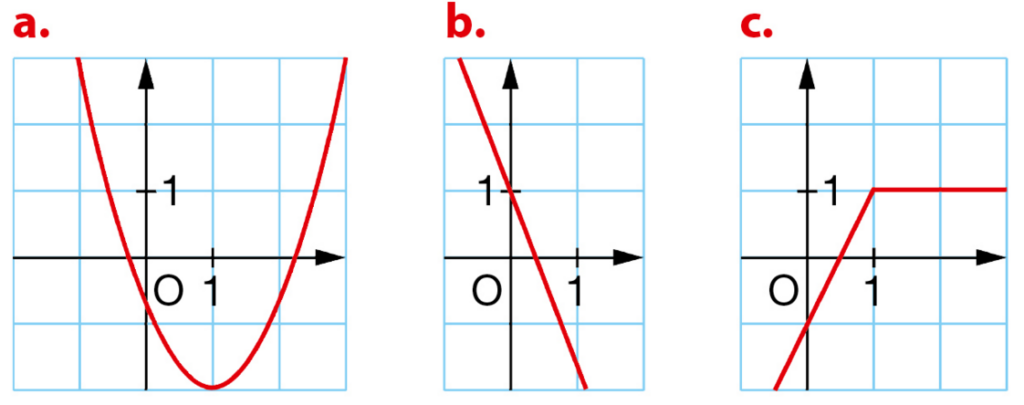
Par lecture graphique, indiquer pour chaque fonction affine, quelle droite est sa représentation graphique.

Exercice 2 :

Déterminer la fonction affine f telle que f(9)=-1 et f(18)= – 8.

Exercice 3 :

f est la fonction affine définie par : $f(x)\,=-3x\,+\,2$ .
a. Calculer l’image de —4 par f.
b. Déterminer l’antécédent de 5 par f.

Exercice 4 :

g est la fonction affine définie par :

$g(x)\,=\,4x\,+3$ .
1. Calculer l’image par g de:
a. 2 b.0 c.-8

2. Déterminer l’antécédent par g de:
a.0 b.9 c.—1

Exercice 5 :

h est la fonction affine $x\,\mapsto \,5x-4$ .
Recopier et compléter le tableau suivant :

Exercice 6 :

g est la fonction affine $x\,\mapsto \,-2x-1$ .
Amar affirme : « L’image d’un nombre par g est toujours négative. »
Que peut-on en penser ? Expliquer.

Exercice 7 :

f est la fonction affine $x\,\mapsto \,\frac{1}{4}x-6$ .

Quel programme de calcul faut-il appliquer :
a. pour calculer l’image d’un nombre par f?
b. pour déterminer l’antécédent d’un nombre par f?

Exercice 8 :

Voici des fonctions affines $x\,\mapsto \,ax\,+\,b$ .
Pour chacune d’elles, préciser les valeurs de a et de b.

$a.\,x\,\mapsto \,x+3\,\\b.\,x\,\mapsto \,2x-1\,\\c.\,x\,\mapsto \,2-5x\,\\d.\,x\,\mapsto \,x\,\\e.\,x\,\mapsto \,7\,\\f.\,x\,\mapsto \,-\frac{1}{2}x\,\\g.\,x\,\mapsto \,\frac{x}{3}\,-1\,\\h.\,x\,\mapsto \,-\frac{3}{4}-x\,\\i.\,x\,\mapsto \,7-0,5x$

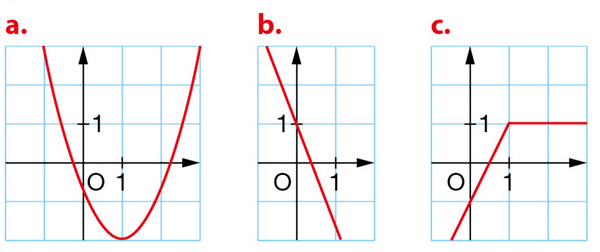
Exercice 9 :

Le graphique peut-il représenter une fonction affine ?

Exercice 10 :

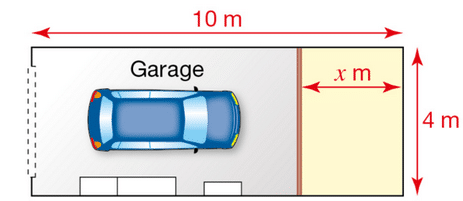
Louise a un garage rectangulaire de 10 m sur 4 m.
Elle veut installer une cloison pour avoir un débarras au fond de son garage comme indiqué ci-dessous.

On note l’aire, en m², de la surface de garage dont elle disposera après l’installation de la cloison.

1. Donner l’expression de .

2. a. Déterminer :
et l’antécédent de 32.
b. Que signifient ces résultats pour la situation ?

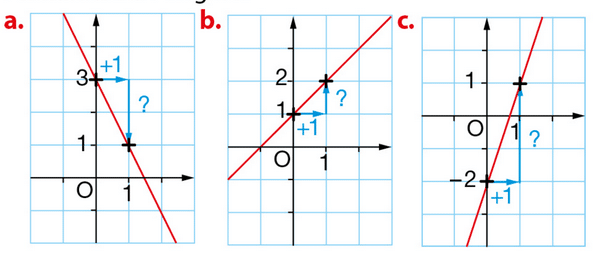
Exercice 11 :

Les droites ci-dessous représentent graphique ment des fonctions affines.
Dans chaque cas, lire le coefficient directeur et l’ordonnée à l’origine.

Exercice 12 :

Voici trois applications affines définies par :

f(x) = 36 ; g(x) = 1,2+ 12 ; h(x) = 2,4.

1) Calculer g(5) et h(5).

2) Sur une feuille de papier millimétré, dans un repère orthogonal, avec 1 cm pour 2 unités sur l’axe des abscisses et 1 cm pour 3 unités sur l’axe des ordonnées, tracer les droites d₁, d₂et d₃ associées respectivement aux applications affines définies par f(x), g(x) et h(x).

3) Déterminer par le calcul les valeurs de pour lesquelles g(x) < f(x).

4) Calculer les coordonnées du point M, intersection des droites d₁ et d₂, et les coordonnées du point N, intersection des droites d₂ et d₃.

Exercice 13 :

I – Le plan est muni d’un repère orthogonal.

(Utiliser une feuille de papier millimétré.)

Prendre sur l’axe des abscisses 2 cm pour une unité.

Prendre sur l’axe des ordonnées 1 cm pour 20 unités.

Graduer l’axe des abscisses de 0 à 5.

Graduer l’axe des ordonnées de 0 à 270.

1) Tracer dans ce repère les droites D₁, D₂ et D₃ d’équations :

D₁ : y = – 90x + 270 (en bleu)

D₂ : y = – 40x + 150 (en rouge)

D₃ : y = – 10x + 50 (en noir)

(Donner les coordonnées de 2 points pour chaque droite.)

2) Calculer les coordonnées de M, point d’intersection de D₁ et de D₂.

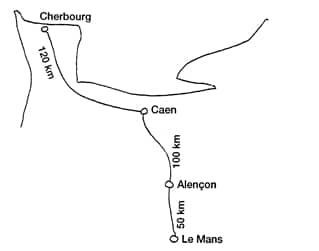
II – Le samedi 18 juin 1995, à 16 h, a été donné le départ de la course automobile des 24 heures du Mans.

Les 3 personnes suivantes s’y sont rendues :

· Hélène est partie de Cherbourg avec sa voiture et a roulé à la vitesse moyenne de 90 km/h.
· Clément est parti de Caen avec son scooter et a roulé à la vitesse moyenne de 40 km/h.
· Adrien est parti d’Alençon à vélo et a roulé à la vitesse moyenne de 10 km/h.

La distance de Cherbourg à Caen est de 120 km. Celle de Caen à Alençon est de 100 km. Celle d’Alençon au Mans est de 50 km.

Les trois personnes ont quitté leur domicile à 8 heures.

On désignera par le temps, en heures, écoulé après 8 heures et par la distance, en km, restant à parcourir pour arriver au Mans.

1) a) Quelle distance Hélène parcourt-elle en heures ?

b) En déduire que, après heures de trajet, la distance qu’il lui reste à parcourir pour arriver au Mans est égale à 270 – 90x.

On notera H(x) = 270 – 90x.

2) Après heures de trajet, quelle distance doit encore parcourir Clément pour arriver au Mans ? On notera cette distance C(x).

De même, après heures de trajet, quelle distance doit encore parcourir Adrien pour arriver au Mans ? On notera cette distance A(x).

3) Quelle interprétation peut-on donner des coordonnées du point M considéré dans la partie I-2) ?

4) Par une lecture du graphique, estimer à quelle distance du Mans, Hélène doublera Adrien. Estimer l’heure de ce dépassement.

5) Par un calcul, déterminer à quelle heure et à quelle distance du Mans Clément doublera Adrien.

Exercice 14 :

Deux villes A et B sont distantes de 92 km.

Un motocycliste part de A et se dirige vers B à la vitesse de 54 km/h.

Au même moment, un automobiliste quitte la ville B pour se rendre en A : il roule à la vitesse de 84 km/h. (Ces vitesses sont supposées constantes durant tout le trajet.)

(Formule : distance parcourue = vitesse x durée du parcours.)

I – 1) a) A quelle distance de la ville A se trouve le motocycliste 10 minutes après son départ ? une demi-heure après son départ ? 40 minutes après son départ ?

b) A quelle distance de la ville A se trouve l’automobiliste 10 minutes après son départ ? une demi-heure après son départ ? 40 minutes après son départ ?

2) Montrer que 54 km/h = 0,9 km/min.

De la même façon, exprimer 84 km/h en km/min.

3) a) Le motocycliste a roulé pendant minutes. Exprimer à l’aide de la distance le séparant de la ville A.

b) L’automobiliste a également roulé pendant minutes. Montrer que la distance le séparant de la ville A est égale à 92 – 1,4x .

c) En déduire l’instant où les deux véhicules vont se croiser.

Il – Le plan est muni d’un repère orthogonal.

Sur l’axe des abscisses, où sont repérées les durées, 1 cm représente 10 minutes.

Sur l’axe des ordonnées, où sont repérées les distances, 1 cm représente 10 kilomètres.

1) Tracer la droite (D₁) d’équation = 0,9, puis la droite (D₂) d’équation = – 1,4x + 92.

2) Les droites (D₁) et (D₂) se coupent en P. Calculer les coordonnées de P

Que représentent les coordonnées de ce point P ?

3) La droite (D₂) coupe l’axe des abscisses en Q.

Lire l’abscisse de Q.

Que représente ce nombre ?

Exercice 15 :

f est la fonction affine $x\,\mapsto \,\frac{1}{4}\,x-6$ .

Quel programme de calcul faut-il appliquer :
a. pour calculer l’image d’un nombre par f?
b. pour déterminer l’antécédent d’un nombre par f?

Exercice 16 :

Le graphique peut-il représenter une fonction affine ?

Exercice 17 :

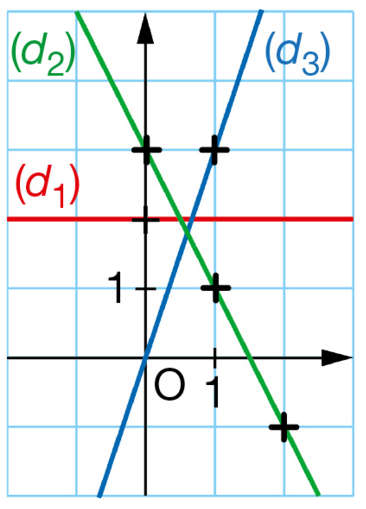
Dans ce repère, les droites (), () et () représentent
graphiquement les fonctions affines respectives et .
1. Parmi ces fonctions, laquelle est linéaire ? constante ?
2. Par chaque fonction, donner :
a. l’image de 1.
b. si possible, l’antécédent de 3.

Exercice 18 :

Un site de stockage de données en ligne propose l’offre suivante :

On note f la fonction qui modélise le montant, en euros, d’une commande de x gigaoctets.
a. Donner l’expression de f(x).
La fonction f est-elle affine ?
b. Calculer l’image de 400 par la fonction f.
Interpréter le résultat pour la situation.
c. Déterminer l’antécédent de 15 par la fonction f.
Interpréter le résultat pour la situation.

Exercice 19 :

Voici le devis établi par un couvreur-zingueur pour refaire la
toiture en tuiles d’une maison.

1.Exprimer le coût pour refaire une toiture de x m².
2.a. Déterminer :

C(120)
l’antécédent de 4 500.

b. Que signifient ces résultats pour la situation ?

Exercice 20 :

Effectuer le QCM sur les fonctions affines suivant :

Télécharger puis imprimer cette fiche en PDF.

Télécharger ou imprimer cette fiche «fonctions affines : exercices de maths en 3ème corrigés en PDF.» au format PDF afin de pouvoir travailler en totale autonomie.

Réviser les cours et exercices avec nos Q.C.M :

Q.C.M en 6ème Q.C.M en 5ème Q.C.M en 4ème Q.C.M en 3ème Q.C.M en 2de Q.C.M en 1ère Q.C.M en Terminale

D'autres ressources pour progresser en autonomie :

Chronomètre Horloge France Tables Multiplication Arrondir des décimaux Rapporteur et Angles Médiatrice Symétrie Axiale d'un triangle Symétrie Centrale d'un triangle Translation d'un triangle Rotation Homothétie Bissectrice Tracer droite parallèle Conversion Aires et Volumes Addition de deux relatifs Soustraction Relatifs Addition et soustraction de trois relatifs Produit Deux Relatifs Produit Trois Relatifs Quotient Relatifs Carré Entier Racine Carrée Théorème Pythagore Liste Diviseurs Décomposition Facteurs Premiers Calcul du PGCD PGCD Algorithme Euclide Test Nombre Premier Déterminer Fonction Linéaire Déterminer Fonction Affine Traceur Courbe Trigonométrie Angle Trigonométrie Longueur Périmètre d'un Cercle Aire d'un Disque Volume du Parallélépipède Rectangle Volume du cylindre Surface d'une Sphère et Volume d'une boule Volume d'une pyramide à base rectangulaire Section d'une pyramide Visualiser Section Cône en 2D Section d'un Cône Carte Mondiale Coordonnées Géographiques

Mathématiques Web c'est 2 250 077 fiches de cours et d'exercices téléchargées.