Homothéties : cours de maths en 3ème avec leçon en PDF en troisième.

Un cours sur les homothéties avec définition de la transformation ainsi que les différentes propriétés de conservation puis les effets sur les agrandissements ou réductions de figures. L’élève devra savoir construire l’image d’une figure par une homothétie de centre O et de rapport k à l’aide du matériel de géométrie (règle, compas, équerre et rapporteur). Savoir interpréter le genre d’homothétie en fonction du signe du rapport mais également, appliquer les différentes propriétés afin d’effectuer des démonstrations. Nous terminerons cette leçon sur les homothéties avec des problèmes concrets de la vie courante en troisième

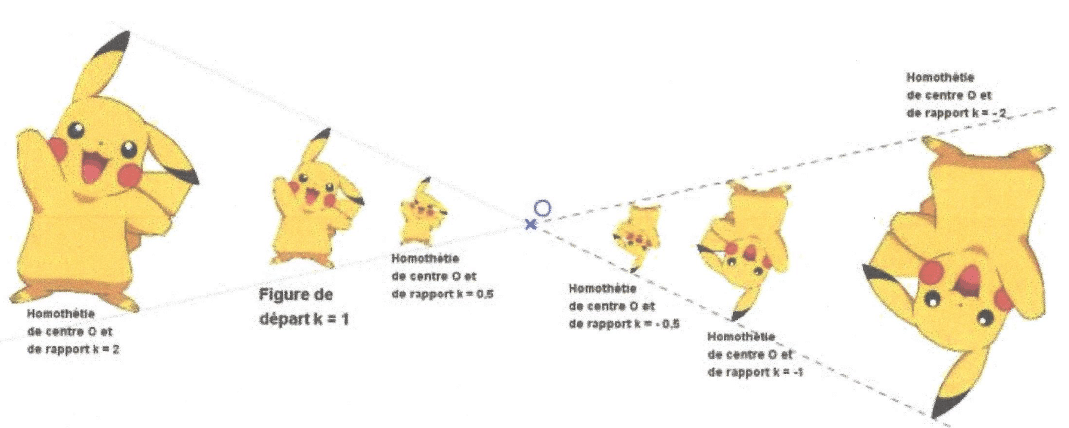
I. L’homothétie :

Définition :

Transformer une figure par une homothétie de centre O, c’est l’agrandir ou la réduire

en faisant glisser les points le long des droites passant par O.

Définition :

L’image d’un point M par l’homothétie de centre O et de rapport k>0 est le point M’ tel que :

M’ appartient à la demi-droite [OM);
$OM'=k\times OM$ .

Propriété :

Une homothétie conserve :

l’alignement;
la mesure des angles
le parallélisme.

Si k >0, alors l’homothétie multiplie :

les longueurs par k;
les aires par .

L’homothétie transforme une droite en une autre droite qui lui est parallèles.

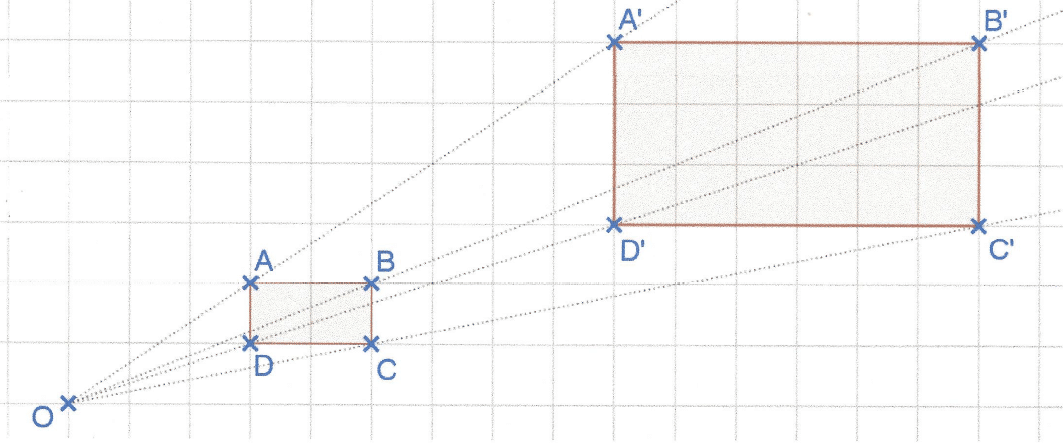
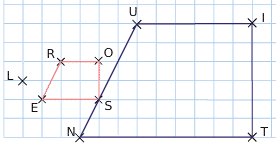
Exemple :

Le rectangle A’B’C’D’ est l’image du rectangle ABCD par l’homothétie de centre O et de rapport k=3.

AB = 2 cm donc $A'B'=3\times AB=3\times 2=6\,cm$ .

$Aire_{ABCD}=2\,cm^2$ donc $Aire_{A'B'C'D'}=3^2\times 2=18\,cm^2$ .

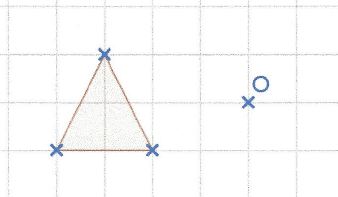
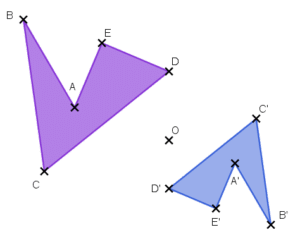
Application 1 :

Construire les images du triangle par les homothéties de centre O et de rapport 3;-1 et – 2.

Remarque :

L’image du triangle de départ par l’homothétie de centre O et de rapport – 1 est en fait une symétrie centrale de centre O.

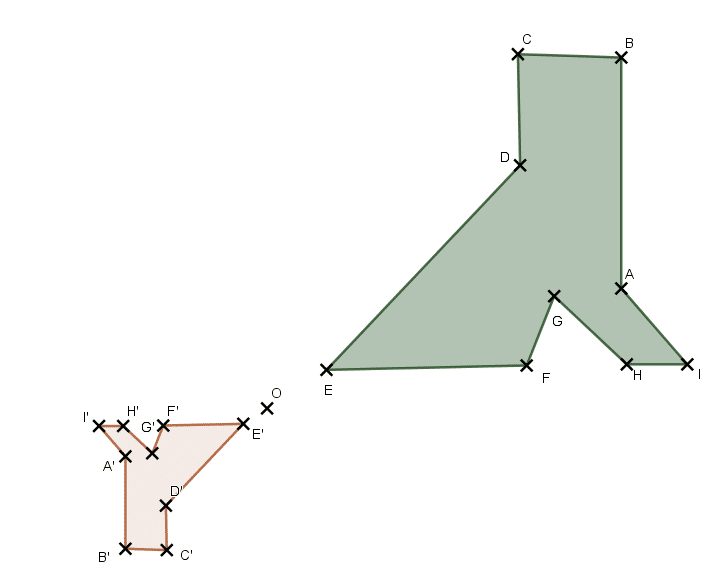
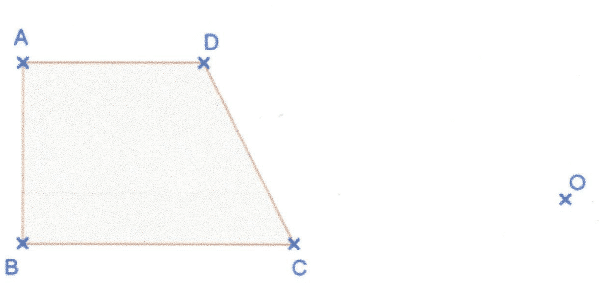
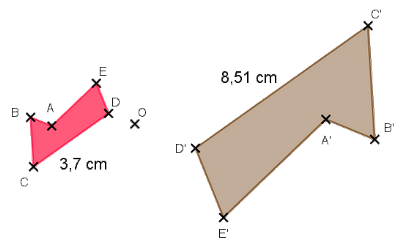
Application 2 :

Construire les images du trapèze rectangle ABCD par les homothéties de centre O et de rapport $\frac{2}{5}$ et – 0,8.

Application 3 :

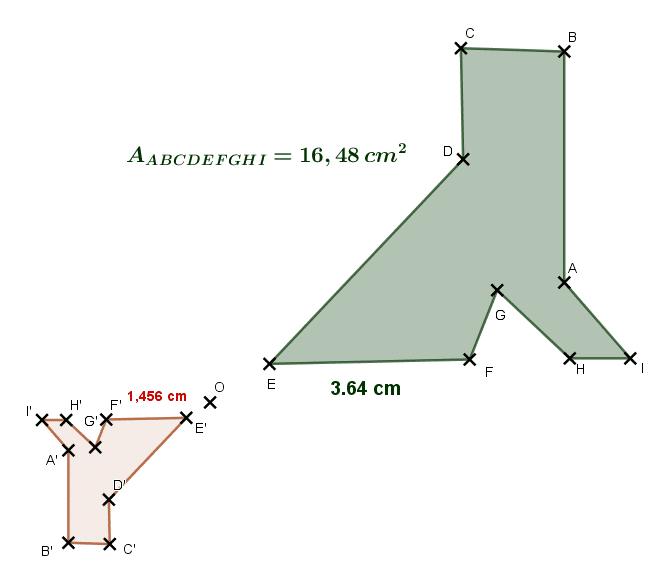
On considère l’homothétie de centre O et de rapport k qui transforme la chaussure verte en la chaussure rouge.

Est-ce un agrandissement ou une réduction ? justifier votre réponse.
Quel est la valeur du rapport k?
Calculer l’aire de la chaussure rouge (arrondir le résultat au centième).

C’est un agrandissement car nous observons que EF = 3,64 cm et E’F’ = 1,46 cm.
$|k |=\frac{E'F'}{EF}=\frac{1,456}{3,64}=0,4$ donc comme $https://mathematiques-web.fr/cgi-bin/mimetex.cgi?Aire_{A'B'C'D'E'F'G'H'I'}=k^2\times \,Aire_{ABCDEFGHI}=(-0,4)^2\times \,16,48=2,6368\approx\,2,64\,cm^2$

4.1/5 - (7 votes)

Télécharger puis imprimer cette fiche en PDF

Télécharger ou imprimer cette fiche «homothéties : cours de maths en 3ème avec leçon en PDF en troisième.» au format PDF afin de pouvoir travailler en totale autonomie.

Télécharger nos applications gratuites Mathématiques Web avec tous les cours,exercices corrigés.

D'autres articles analogues à homothéties : cours de maths en 3ème avec leçon en PDF en troisième.

Mathématique web est un site de mathématiques destinés aux élèves et professeurs du collège (6ème, 5ème, 4ème et 3ème) au lycée (2de, 1ère et terminale. Vous trouverez sur ce site de nombreuses ressources vous permettant de vous familiariser avec les mathématiques. Toutes les cours de maths sont rédigés par des professeurs et sont conformes aux programmes officiels de l'éducation nationale.
Comment réussir en maths ?
Une question régulièrement posée, comme le dit le dicton rien ne tombe du ciel. Afin de combler vos lacunes en mathématiques et d'envisager une progression constante tout au long de l'année scolaire et analogues à homothéties : cours de maths en 3ème avec leçon en PDF en troisième..
Pour celà, il faudra maitriser le contenu de votre leçon (définitions, théorèmes et propriétés) et vous exercer régulièrement sur les milliers d'exercices de maths disponibles sur notre site et vous pourrez également, consulter le corrigé de chaque exercice afin de repérér vos différentes erreurs et par conséquent, développer des compétences en maths.
De nombreux exercices de maths pour tous les niveaux similaires à ceux de votre manuel scolaire ainsi que, toutes les leçons du collège au lycée rédigées par des enseignants titutaires de l'éducation nationale similaires à homothéties : cours de maths en 3ème avec leçon en PDF en troisième..
En complément, vous trouverez de nombreux exercices de programmation et d'algorithme réalisés avec le programme scratch ainsi que de nombreux sujets de contrôles de maths afin de vous préparer le jour d'un devoir surveillé en classe.
Toutes les fiches ( cours et exercices) sont à télécharger gratuitement en PDF afin de pouvoir les imprimer librement sur des supports similaires à ceux de votre manuel scolaire.

Théorème de Thalès : cours de maths en troisième (3ème)
87
Un cours de mathématiques en troisième sur le théorème de Thalès. Ce cours de maths fait intervenir les notions suivantes : - configurations de Thalès; - partie directe et réciproque; - Produit en croix. Ce cours de mathématiques sur le théorème de Thalès a été rédigé par un enseignant de l'éducation…
Probabilités : cours de maths en 3ème avec leçon en PDF en troisième.
84
Cours de maths en classe de troisième (3ème) sur les probabilités et les expériences aléatoires, définition de l'événement, des issues et du calcul de probabilités à une et deux épreuves. I. Notion de probabilités 1. Les issues et arbre de probabilité Définitions : Une expérience est dite aléatoire lorsque l'on…
Fonctions affines : cours de maths en 3ème avec leçon en PDF.
84
Cours sur les fonctions affines avec la définition, le vocabulaire et les différentes propriétés de ces fonctions. Etude de la courbe représentative et du sens de variation. L'élève devra être capable de calculer une image ou un antécédent mais, également, savoir tracer la courbe d'une fonction affine à l'aide de…
Fonctions : cours de maths en 3ème avec leçon en PDF en troisième.
83
Un cours sur les généralités des fonctions avec la définition d'un antécédent, d'une image et de l'étude de la courbe représentative d'une fonction en 3ème. L'élève devra savoir calculer l'image d'un nombre par une fonction mais aussi déterminer un antécédent par le calcul ou en exploitant la courbe représentative de…
Volumes : cours de maths en 3ème avec leçon en PDF en troisième.
82
Cours sur les formules du volume d'un solide et l'étude de sections de solides dans l'espace avec des situations de réduction ou d'agrandissement en troisième (3ème). L'élève devra connaître ses formules par coeur et savoir représenter des solides dans l'espace avec la perspective cavalière ou encore, savoir dessiner son patron.…

Les dernières fiches mises à jour

Mathématiques Web c'est 2 048 880 fiches de cours et d'exercices téléchargées.
Rejoignez les 46 075 membres de Mathématiques Web, inscription gratuite.