L’élève devra connaître ses formules par cœur et savoir représenter des solides dans l’espace avec la perspective cavalière ou encore, savoir dessiner son patron. Il doit aussi développer des compétences sur les volumes de solides en effectuant des conversions de grandeurs ou en appliquant les formules du volume d’un cube, d’une pavé droit, d’une cône ou encore d’une pyramide. Nous terminerons cette leçon sur les volumes et sections de solides avec des exemples concrets issus de la vie courante en troisième.
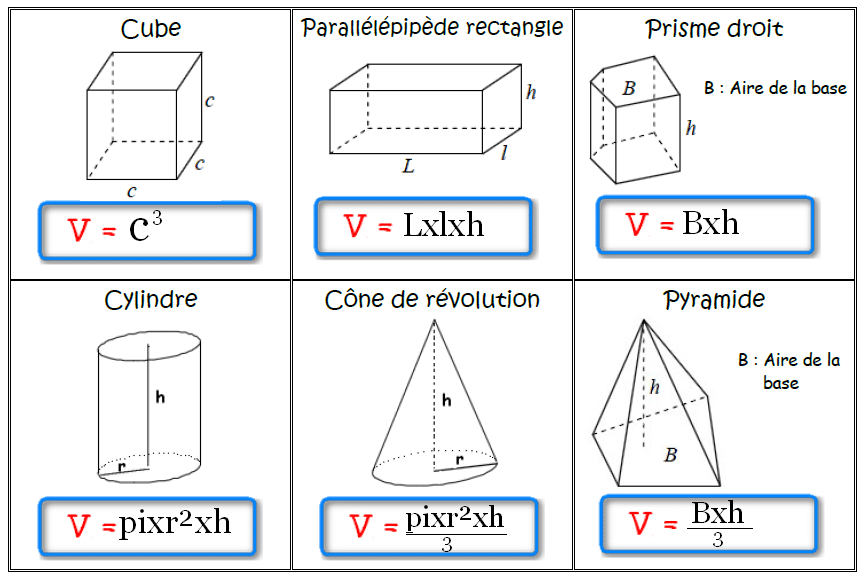
I. Formules de calculs de volumes de solides dans l’espace
II. Sections planes de solides
1.Section d’un pavé droit par un plan
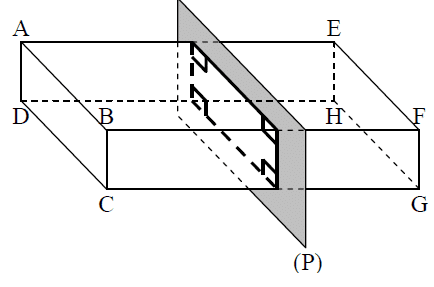
La section d’un pavé droit par un plan (P) parallèle à une face est un rectangle identique
à cette face :
La section d’un pavé droit par un plan (P) parallèle à une arête est un rectangle : 
2.Section d’un cylindre de révolution par un plan
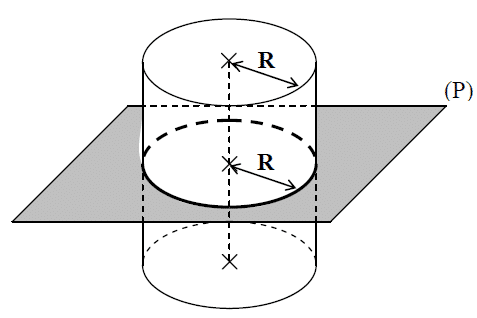
La section d’un cylindre de révolution de rayon R par un plan (P) parallèle aux bases est un cercle de rayon R :
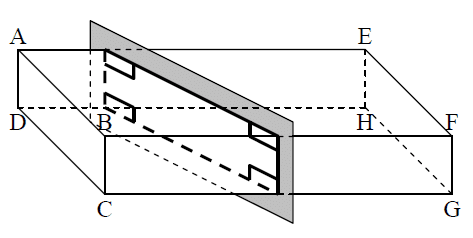
La section d’un cylindre de révolution par un plan (P) parallèle à l’axe est un rectangle :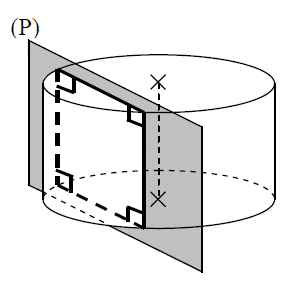
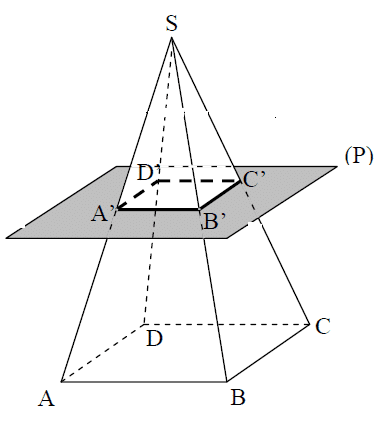
3.Section d’une pyramide par un plan
La section d’une pyramide par un plan (P) parallèle à la base est un polygone ayant la même forme que la base
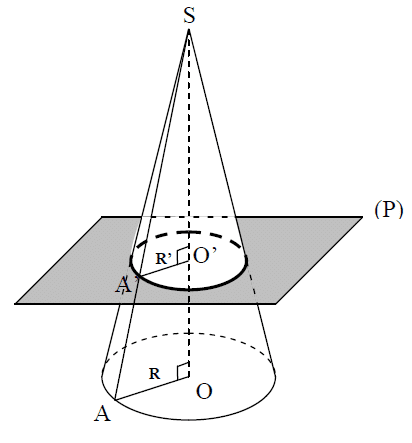
4.Section d’un cône de révolution par un plan
La section d’un cône de révolution par un plan (P) parallèle à la base est un cercle dont
le centre appartient à la hauteur du cône.
II. Les agrandissements et les réductions
Lorsque deux figures ont la même forme, on peut calculer le coefficient suivant :
- si k >1, on dit qu’il s’agit un agrandissement ;
- si k <1, on dit qu’il s’agit d’une réduction.
Dans un agrandissement ou une réduction de rapport k :
- les longueurs sont multipliées par k ;
- les aires sont multipliées par ;
- les volumes sont multipliés par .
Exemple :
Considérons une pyramide de volume subissant un agrandissement de rapport k=4
alors le volume V’ après agrandissement de cette pyramide sera :.
Télécharger ou imprimer cette fiche «volumes : cours de maths en 3ème en PDF.» au format PDF afin de pouvoir travailler en totale autonomie.
D'autres cours et exercices à consulter
- Homothéties : cours de maths en 3ème en PDF.
- Statistiques : cours de maths en 3ème en PDF.
- Probabilités : cours de maths en 3ème en PDF.
- Fonctions affines : cours de maths en 3ème en PDF.
- Fonctions linéaires : cours de maths en 3ème en PDF.
- Les équations : cours de maths en 3ème en PDF.
- Calcul littéral : cours de maths en 3ème en PDF.
- Fonctions : cours de maths en 3ème en PDF.
