Probabilités : cours de maths en 3ème à télécharger en PDF.

Sommaire de cette fiche

Les probabilités et les expériences aléatoires à travers un cours de maths en 3ème contenant la définition de l’événement, des issues et du calcul de probabilités à une et deux épreuves est très important. Il faut rester bien concentré pour maîtriser ce chapitre.

I. Notion de probabilités

1. Les issues et arbre de probabilité

Définitions :

Une expérience est aléatoire lorsque l’on ne peut pas prévoir à l’avance quel va être son résultat parmi les différentes issues possibles.
La schématisation qui nous permet de visualiser les différentes issues possibles d’une expérience aléatoire s’appelle l’arbre de probabilité.
Chaque branche de cet arbre de probabilités indique la probabilité d’une issue.
On dit que l’arbre est pondéré par les probabilités.

Exemple :

Katia lance un dé équilibré à six faces numérotées 1,2,2,3,3 et 3.

On observe le nombre indiqué sur la face supérieure : les issues sont 1,2 et3.

Le dé est équilibré, donc chaque face a autant de chance de sortir qu’une autre.

Ainsi, la probabilité de sortie du nombre 1 est de $\frac{1}{6}$ , puisqu’une seule face du dé porte le numéro 1.
Deux faces portent le numéro 2, donc la probabilité de l’issue 2 est $\frac{2}{6}$ soit $\frac{1}{3}$ .
De même, celle de l’issue 3 est $\frac{3}{6}$ soit $\frac{1}{2}$ soit encore 0,5 ou 50 %

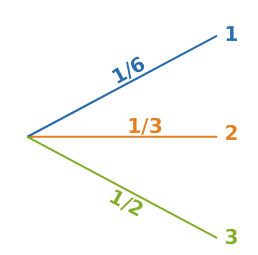
On résume ces résultats sur l’arbre de probabilité ci-dessous :

Propriétés :

Une probabilité est un nombre qui est compris entre 0 et 1.
La probabilité s’exprime par un nombre en écriture fractionnaire, en écriture décimale, ou bien encore sous forme d’un pourcentage.

2.Les événements

Définitions :

Un événement réalisé par aucune issue s’appelle un événement impossible et sa probabilité est 0.
Un événement réalisé par toute les issues s’appelle un événement certain et sa probabilité est 1.
L’événement contraire à un événement A, noté $\overline{A}$ , est réalisé lorsque A ne l’est pas.

Propriétés :

La probabilité d’un événement est la somme des probabilités des issues qui le réalisent.

la somme des probabilités d’un événement et de son contraire est égale à 1.

$P(A)+P(\overline{A})=1$ .

Définition :

Deux événements sont incompatibles lorsqu’ils ne peuvent se réaliser en même temps.

Exemple :

Pour le dé de Katia, l’événement « obtenir un nombre pair » et l’événement « obtenir le 3 » sont incompatibles.

3.Des fréquences aux probabilités

Lorsque aucune considération de régularité ou de symétrie ne permet de connaître la probabilité d’une issue, on peut l’estimer en effectuant un grand nombre de fois une expérience aléatoire.

Propriété :

Soient une expérience aléatoire et un événement A dont la probabilité se note P(A).

Lorsqu’on réitère un très grand nombre de fois cette expérience aléatoire, la fréquence d’apparition de l’événement A a tendance à se stabiliser autour de P(A).

Exemple :

En lançant un grand nombre de fois un bouchon de la même façon, on pourrait ainsi estimer

la probabilité qu’il retombe dans l’une ou l’autre des positions ci-dessous :

Télécharger puis imprimer cette fiche en PDF.

Télécharger ou imprimer cette fiche «probabilités : cours de maths en 3ème en PDF.» au format PDF afin de pouvoir travailler en totale autonomie.

Vous devez vous inscrire ou vous connecter à votre compte afin de pouvoir télécharger ce document au format PDF.

D'autres cours et exercices à consulter

Mathématiques Web c'est 2 268 671 fiches de cours et d'exercices téléchargées.