Trigonométrie : exercices de maths en 3ème corrigés en PDF.

La trigonométrie dans le triangle avec des exercices de maths en 3ème corrigés.

Dans cette série d’énoncés, vous retrouverez les notions notions suivantes :

triangle rectangle : côté adjacent, opposé et hypoténuse;
cosinus (cos) d’un angle aigu;
sinus (sin) d’un angle aigu;
tangente (tan) d’un angle aigu;
formule algébrique en trigonométrie;
triangle rectangle, trigonométrie et angle aigu.

Ces énoncés corrigés sur la trigonométrie dans le triangle rectangle ont été rédigé par un enseignant et sont à consulter en ligne ou à télécharger au format PDF.

Exercice 1 :

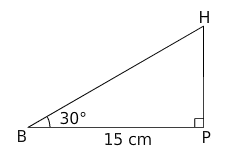
Pour propulser des billes, Mathieu a construit un plan incliné de 30° dont la

base mesure 15 cm de long.

Quelle est la longueur de la pente?

Donner l’arrondi au millimètre.

Exercice 2 :

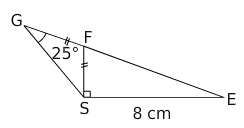
Sachant que les points E, F et G sont alignés, on veut calculer la longueur FS.

1.Calculer la mesure de l’angle $\widehat{GFS}$ .

2.Calculer la mesure de l’angle $\widehat{SFE}$ .

3.En déduire l’arrondi au dixième de FS.

Exercice 3 :

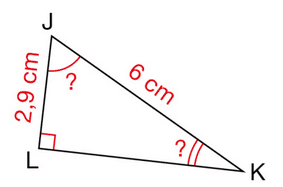
a. Utiliser les données de cette figure pour donner une valeur approchée au degré près de la
mesure de l’angle $\widehat{LJK}$ .

b.En déduire une valeur approchée de la mesure de l’angle $\widehat{LKJ}$ .

Exercice 4 :

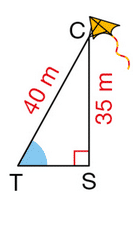
Tania fait voler son cerf-volant.
La ficelle a une longueur TC de 40 m.

Elle est tendue et le cerf-volant est à 35 m du sol.
Donner une valeur approchée au degré près de la mesure de l’angle $\widehat{STC}$ .

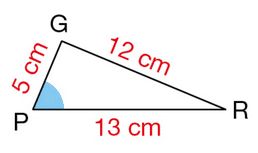
Exercice 5 :

1. Pourquoi le triangle PGR ci-dessous est-il rectangle ?

2. Donner sous forme de fraction irréductible la valeur de:
a. $cos (\widehat{GPR})$ b. $sin (\widehat{GPR})$ c. $tan(\widehat{ GPR})$

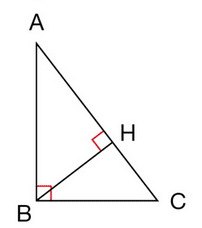
Exercice 6 :

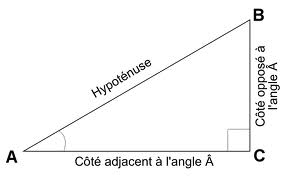
1. Dans le triangle ABC rectangle en B, quel segment est :

a. l’hypoténuse ?

b. le côté adjacent à l’angle $\widehat{BAC}$ ?
c. le côté opposé à l’angle $\widehat{BCA}$ ?
2. Dans le triangle BHC rectangle en H, quel angle a pour côté opposé :
a. [BH]? b. [CH]?

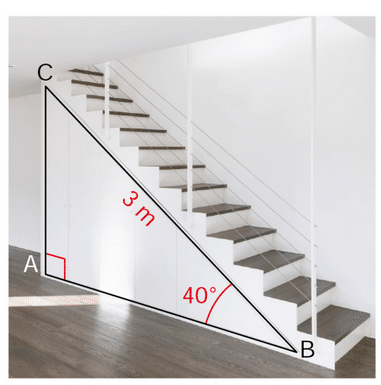
Exercice 7 :

Pour accéder à sa mezzanine, Lola doit installer un escalier.
Avec les données de cette figure, donner une valeur approchée au centième près de la longueur AB, en m.

Exercice 8 :

La tour du One World Trade Center a été inaugurée en 2014, à New York (États-Unis).

Une personne de 1,65 m, située à 100 m de la tour, mesure $\widehat{HOP} = 79,5 ^{\circ}$ (O représente son œil).

Calculer une valeur approchée à l’unité près de la hauteur, en m, de cette tour.

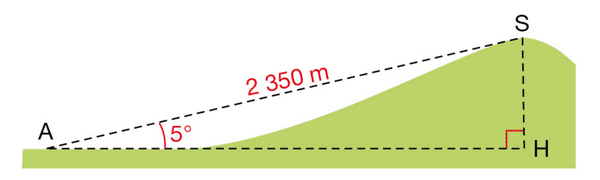
Exercice 9 :

Un géomètre, positionné en A, souhaite calculer l’altitude du sommet S d’une colline.

Son GPS lui indique qu’il se trouve lui-même à une altitude de 625 m.

Il effectue les mesures suivantes :

a. Donner une valeur approchée au centième près de la hauteur HS, en m, de la colline.
b. En déduire l’altitude du point S.

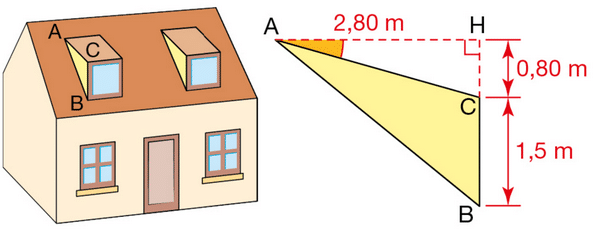
Exercice 10 :

Voici un plan de coupe de l’une des deux lucarnes de cette maison.

Déterminer une valeur approchée au degré près de :
a. la mesure de $\widehat{HAC}$ ,
b. la mesure de $\widehat{HAB}$ .

Exercice 11 :

1) Construire un triangle IJK tel que :

JK = 8 cm ; IJ = 4,8 cm ; KI = 6,4 cm.

2) Démontrer que le triangle IJK est un triangle rectangle.

3) Calculer la mesure en degrés de l’angle $\widehat{IJK}$ .

Donner la valeur arrondie au degré le plus proche.

Exercice 12 :

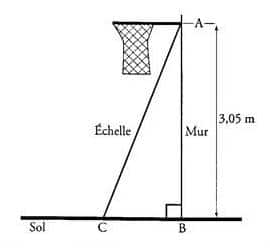
1. Paul veut installer chez lui un panier de basket. Il doit le fixer à 3,05 m du sol. L’échelle dont il se sert mesure 3,20 m de long.

À quelle distance du pied du mur doit-il placer l’échelle pour que son sommet soit juste au niveau du panier ? (Donner une valeur approchée au cm près.)

2. Calculer l’angle formé par l’échelle et le sol. (Donner une valeur approchée au degré près.)

Exercice 13 :

Soit ABC un triangle isocèle de base [BC], [AH] la hauteur issue du sommet A.

On a : BC = 8 cm et AH = 7 cm.

1) Construire le triangle ABC en justifiant la construction.

2) Calculer $tan(\widehat{B})$ .

3) En déduire la valeur de l’angle $\widehat{B}$ arrondie au degré près.

Exercice 14 :

La figure ci-dessous représente un triangle SET isocèle en E, et la hauteur [SH] issue de S. On ne demande pas de refaire la figure.

On sait que les segments [ES] et [ET] mesurent 12 cm et que l’aire du triangle SET est 42 cm².

1) Démontrer que la mesure h du segment [SH] est égale à 7 cm.

2) Calculer la valeur arrondie au millimètre près de la longueur EH.

3) Calculer la mesure arrondie au degré près de l’angle $\widehat{SET}$ .

Exercice 15 :

L’unité de longueur est le centimètre ; l’unité d’aire est le centimètre carré.

On considère la figure ci-contre :

· le triangle ABC est rectangle en A ;
· AB = 3,6 ;
· BC = 6.

1) Calculer la mesure de l’angle $\widehat{ACB}$ (on donnera l’arrondi au degré).

2) Calculer AC.

3) Calculer l’aire du triangle ABC.

4) Soit H le projeté orthogonal du point A sur la droite (BC).

Exprimer l’aire du triangle ABC en fonction de AH.

5) En déduire AH.

Exercice 16 :

ABCD désigne un rectangle tel que AB = 7,2 cm et BC = 5,4 cm.

1) Dessiner en grandeur réelle ce rectangle et sa diagonale [AC].

2) Calculer la mesure arrondie au degré de l’angle $\widehat{ACD}$ .

3) Démontrer que les angles $\widehat{ACD}$ et $\widehat{CAB}$ sont égaux.

4) La médiatrice du segment [AC] coupe la droite (AB) en E. Placer le point E et montrer que le triangle ACE est isocèle.

5) En déduire une valeur approchée de la mesure de l’angle $\widehat{DCE}$ .

3.2/5 - (91 votes)

Télécharger puis imprimer cette fiche en PDF.

Télécharger ou imprimer cette fiche «trigonométrie : exercices de maths en 3ème corrigés en PDF.» au format PDF afin de pouvoir travailler en totale autonomie.

D'autres cours et exercices à consulter

Mathématiques Web c'est 2 268 028 fiches de cours et d'exercices téléchargées.