Produit scalaire : exercices de maths en terminale corrigés en PDF.

Le produit scalaire dans le plan et dans l’espace avec des exercices de maths en terminale qui vous donneront la possibilité de vous exercer et de réviser ce chapitre en ligne.

Cette fiche fait intervenir les notions suivantes :

définition du produit scalaire;
propriété de bilinéarité du produit scalaire;
symétrie du produit scalaire;
produit scalaire dans le plan et l’espace.

L’élève devra être capable d’utiliser les propriétés de linéarité et de symétrie du produit scalaire afin d’étudier des situations de parallélisme ou d‘’orthogonalité. Ces exercices sont accompagnés de leur correction afin que vous pointiez vos difficultés en terminale.

Exercice n° 1 :

Dans un repère orthonormé de l’espace le vecteur $\vec{u}$ a pour coordonnées (1;2;4).

Calculer $\| \vec{u} \|$ .

Exercice n° 2 :

Dans un repère orthonormé de l’espace, A et B sont les points de coordonnées respectives

(3;1;0) et (5;0;1).

Calculer $\| \vec{AB} \|$ .

Exercice n° 3 :

$\vec{u}$ et $\vec{v}$ sont deux vecteurs de l’espace tels que $\| \vec{u} \|=1$ , $\| \vec{v} \|=2$ et $\| \vec{v}-\vec{u} \|=\sqrt{5}$ .

Calculer $\vec{u}.\vec{v}$ .

Exercice n° 4 :

$\vec{AB}$ et $\vec{AC}$ sont deux vecteurs de l’espace tels que AB = 5, AC = 8 et $\vec{BAC}=60 ^{\circ}$ .

Calculer $\vec{AB}.\vec{AC}$ .

Exercice n° 5 :

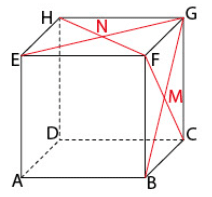
ABCDEFGH est un cube de côté .

Les points M et N sont les centres des faces BCGF et EFGH.

a) Vérifier que $AM^2=\frac{3}{2}a^2$ .

b) Calculer et .

c) En déduire la valeur du produit scalaire $\vec{AM}.\vec{AN}$ .

Exercice n° 6 :

Dans un repère orthonormé de l’espace, on donne les coordonnées des vecteurs $\vec{u}$ et $\vec{v}$ .

Calculer $\vec{u}.\vec{v}$ .

$a)\\,\vec{u}(2;3;-1)\vec{v}(1;0;2)\\b)\vec{u}(0;-2;5)\vec{v}(6;1;1)\\c)\vec{u}(1;-1;2)\vec{v}(3;-1;1)$

Exercice n° 7 :

Dans un repère orthonormé, on considère les points A(1;-1;0), B(-2,2,6), C(3,1,- 8)

et le vecteur $\vec{n}(3,1,1)$ .

1.Vérifier que les points A,B,C ne sont pas alignés.

2.a) Démontrer que le vecteur $\vec{n}$ est normal au plan ABC.

b) Déterminer une équation cartésienne du plan (ABC).

Exercice n° 8 :

Dans un repère orthonormé, A et B sont les points de coordonnées respectives

(3,2,0) et (5,1,-1) .

$\rho$ est le plan passant par A et orthogonal à la droite (AB).

a. Donner un vecteur normal au plan $\rho$ .

b. En déduire une équation cartésienne du plan $\rho$ .

Exercice n° 9 :

Soit les points de l’espace A(-4;4;0), B(4;0;-4) et C(1;1;1)

1. Déterminer une représentation paramétrique de la droite (AB).

2. Déterminer la distance entre le point C et son projeté orthogonal H sur la droite (AB).

H est tel que les droites (CH) et (AB) sont perpendiculaires.

Exercice n° 10 :

Soit P le plan passant par le point A (4; 8;-4) et dirigé par les vecteurs $\vec{u}$ (2 ; -1 ; 3) et $\vec{v}$ (4; 1; -3).
1. Démontrer que $\vec{n}$ (0 ; 3 ; 1) est un vecteur normal au plan P.
2. Déterminer un vecteur normal $\vec{n_1}$ au plan P, tel que la troisième coordonnée de $\vec{n_1}$ , soit égale 7.
3. Déterminer un vecteur normal $\vec{n_2}$ du plan P, tel que la deuxième coordonnée de $\vec{n_2}$ , soit égale – 1.
4. Est-il possible de trouver un vecteur normal au plan P dont la première coordonnée est égale à 4 ?

Exercice n° 11 :

Soit (d) la droite dont une représentation paramétrique est :

$\{\begin{matrix} x=3-2t\\ y=1+5t\\z=-7+6t \end{matrix}.$ avec $t\in \mathbb{R}$ .
Déterminer une équation du plan P passant par le point A(8;-5 ;3) et perpendiculaire à la droite (d).
Exercice n° 12 :

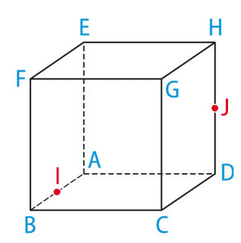
ABCDEFGH est un cube.

Le point I est le milieu de [AB] et le point J est le milieu de [DH].
On se place dans le repère orthonormé $(A ; \vec{AB}, \vec{AD}, \vec{AE})$ .
1. Déterminer les coordonnées des points I, Jet G.
2. Justifier que les points I, J et G définissent un plan.
3. a. Déterminer des réels a, b et c tels que $\vec{n}(a ; b ; c)$ soit un vecteur normal au plan (IJG).
b. En déduire une équation du plan (IJG).

Exercice n° 13 :

Soit P le plan d’équation .
Les droites et sont définies par une représentation paramétrique donnée ci-dessous :

$(d_1):\{\begin{matrix} x=5+4t \\ y=2+t\\z=9-t \end{matrix}.$ et $(d_2):\{\begin{matrix} x=2+3t \\ y=2t\\z=1+5t \end{matrix}.$ avec $t\in \mathbb{R}$ .

1. Le plan P et la droite (d1) sont-ils sécants ?
2. Déterminer l’intersection du plan P et de la droite (d2).

Exercice n° 14 :

On considère les points A(0;4;1), B(1;3;0), C(2;-1;-2) et D(7;- 1;4).
1. Démontrer que les points A, B et C ne sont pas alignés.
2. Soit $\Delta$ la droite passant par le point D et de vecteur directeur $\vec{u}$ (2 ; —1 ; 3).
a. Démontrer que la droite $\Delta$ est orthogonale au plan (ABC).
b. En déduire une équation cartésienne du plan (ABC).
c. Déterminer une représentation paramétrique de la droite $\Delta$ .
d. Déterminer les coordonnées du point H, intersection de la droite $\Delta$ et du plan (ABC).
3. Soit le plan d’équation x + y + z = 0 et le plan d’équation x +4y +2=0.
a. Démontrer que les plans et sont sécants.
b. Vérifier que la droite (d), intersection des plans et a pour représentation paramétrique

$\{\begin{matrix} x=-4t-2 \\ y=t\\z=3t+2 \end{matrix}.$

c. La droite (d) et le plan (ABC) sont-ils sécants ou parallèles ?

4/5 - (15 votes)

Télécharger puis imprimer cette fiche en PDF.

Télécharger ou imprimer cette fiche «produit scalaire : exercices de maths en terminale corrigés en PDF.» au format PDF afin de pouvoir travailler en totale autonomie.

D'autres cours et exercices à consulter

Mathématiques Web c'est 2 268 028 fiches de cours et d'exercices téléchargées.