Les identités remarquables et le calcul littéral avec des exercices de maths en 3ème corrigés. Ces fiches sont destinés aux enseignants et aux élèves de troisième désireux de réviser le chapitre. Pour poursuivre les notions vues en cinquième (simple distributivité) et en quatrième ( double distributivité), Vous retrouverez dans cette série les notions suivantes :
- définition d’une expression algébrique ou littérale;
- réduire et développer une expression littérale;
- factoriser une expression littérale;
- substitution.
Ces énoncés corrigés ont été rédigé par un enseignant et sont à consulter en ligne ou à télécharger au format PDF.
Exercice 1 :
Développer puis réduire chaque expression.
Exercice 2 :
Développer et réduire l’expression suivante :
Exercice 3 :
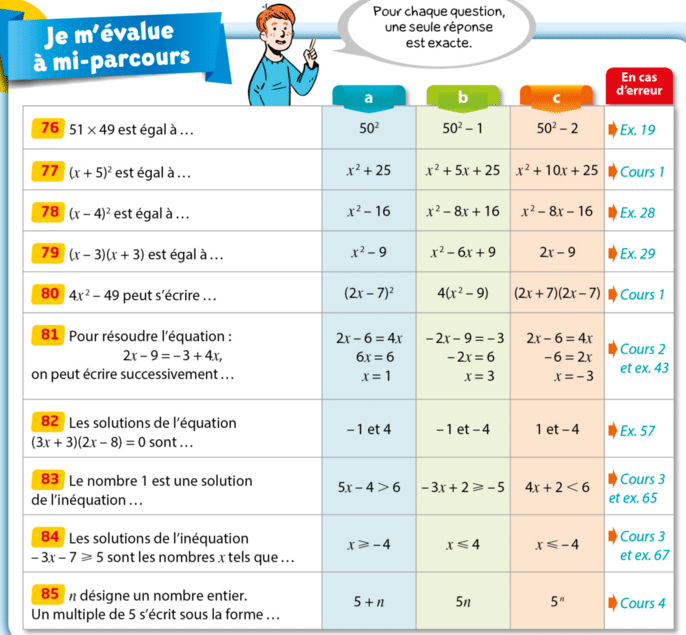
Dans chaque cas, une seule réponse est exacte.
Recopier la bonne réponse.
a. Si l’on développe et réduit l’expression (x + 2)(3x-1),
on obtient :
ou ou
b. La forme développée de est:
ou ou .
c. Une expression factorisée de est:
ou ou .
d. Une expression factorisée de est :
ou ou .
Exercice 4 :
a. Donner le résultat fourni par le programme de calcul si l’on choisit comme
nombre de départ :
-2 ; 5 puis 10.
b. Montrer que le résultat obtenu est toujours le carré d’un nombre entier.
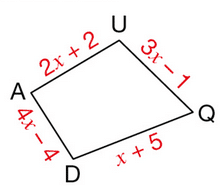
Exercice 5 :
L’unité de longueur est le centimètre.
x désigne un nombre (x > 1).
a. Pour quelle valeur de x le périmètre du quadrilatère QUAD est-il 32 cm ?
b. Quelle est alors la nature quadrilatère QUAD ?
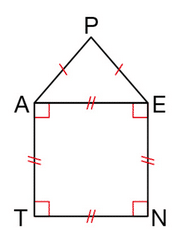
Exercice 6 :
AENT est un carré dont le périmètre est 56 cm.
PAE est un triangle isocèle en P.
a. Calculer AE.
b. Pour quelle longueur de [AP] le périmètre du pentagone PENTA est-il égal à 60 cm ? Justifier.
Exercice 7 :
Développer les expressions littérales suivantes :
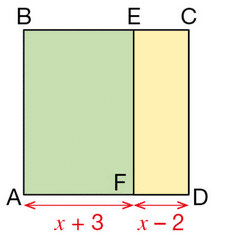
Exercice 8 :
x désigne un nombre supérieur ou égal à 2.
ABCD est un carré et ABEF est un rectangle.
1. Exprimer en fonction de x;
a. la longueur AD ;
b. l’aire du carré ABCD ;
c. l’aire du rectangle ABEF ;
d. l’aire ‘ du rectangle ECDF.
2. a. Exprimer les aires et et leur somme sous forme développée et réduite.
b. Vérifier que cette somme est égale à .
Exercice 9 :
Voici deux programmes de calcul.
a. Appliquer chaque programme aux nombres :
3 ; 10 et – 5 puis à un autre nombre choisi au hasard
Que constate-t-on ? Émettre une conjecture.
b. On note n le nombre choisi au départ.
Exprimer en fonction de n le résultat obtenu avec chaque programme.
Démontrer la conjecture émise à la question a.
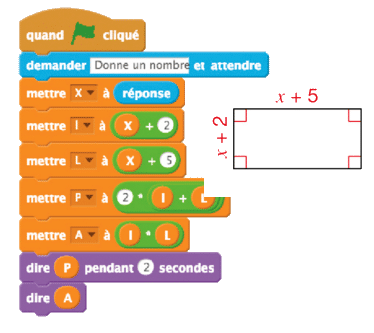
Exercice 10 :
x désigne un nombre positif.
Voici un rectangle dont les côtés ont des longueurs variables.
a. Léa a construit le programme ci-dessous avec le logiciel Scratch.
Que représentent les variables l et L ?
b. Quel est le rôle du programme de Léa ?
c. Léa affirme :«.»
A-t-elle raison ? Expliquer.
d. Réaliser ce programme. Le tester en donnant à x la valeur 3, puis la valeur 10.
Exercice 11 :
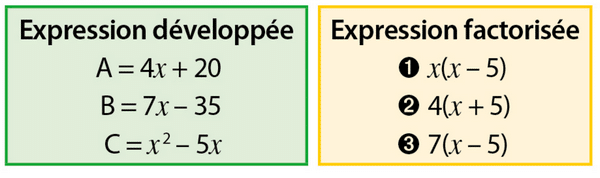
Associer chaque expression de gauche à sa forme factorisée de droite.
Exercice 12 :
. .4) Calculer C pour .
Exercice 13 :
Développer à l’aide du modèle indiqué.
Carré d’une somme | Carré d’une différence
|
Exercice 14 :
On sait qu’en multipliant la somme de deux nombres par leur différence, on obtient :
Développer:
I=(x+8)(x-8) et J=(t-5)(t+5).
Exercice 15 :
Factoriser chaque expression avec une identité remarquable.
Exercice 16 :
Reconnaître une différence de deux carrés dans chaque expression, puis factoriser.
Exercice 17 :
Réduire chaque expression à l’aide d’une identité remarquable.
Exercice 18 :
Développer et réduire chaque expression.
Exercice 19 :
x désigne un nombre relatif.
En utilisant des identités remarquables, recopier et compléter le tableau ci-dessous.
Exercice 20 :
Recopier et compléter à l’aide d’une identité remarquable.
a.
b.
c.
d.
Exercice 21 :
Exercice 22 :
- Rappeler les trois identités remarquables.
- On veut développer :
- Laquelle va-t-on utiliser ? Préciser alors la valeur de a et de b.
- Quel est le développement de ?
Exercice 23 :
Compléter et terminer les développements :
a. ;
b.
Exercice 24 :
Même exercice que le précédent.
a.
b.
Exercice 25 :
Développer :
Exercice 26 :
Développer :
Exercice 27 :
Développer puis réduire :
Exercice 28 :
Indiquer la forme factorisée de ces identités remarquables développées :
Exercice 29 :
Factoriser les expressions suivantes :
Exercice 30 :
1) Développer puis réduire .
2) On pose .
3) Sans utiliser la calculatrice et en se servant de la question 1, trouver la valeur de D.
Exercice 31 :
On donne .
1) Développer et réduire E.
2) Factoriser E.
3) Développer l’expression obtenue à la question 2.
Quel est le résultat
Exercice 32 :
On donne .
1) Montrer que E peut s ‘écrire .
2) Calculer E pour : ; .
3) Factoriser E. Développer l’expression obtenue.
Quel est le résultat?
Exercice 33 :
- Réduire les expressions suivantes :
| A = 3x – 8 + 4x + 5 | B = 3x² + 5x – 6 – 2x² –4x – 3 | C = 5x² – 7 – 9x² +x – 3x + 9 |
| D = 4x² – (5x + x² – 6x) + 7x | E = 3x – (4 + 2x) + (x² + 7) | F = 3x² – (4x – 1) – (x² +5x) |
- Substituer à x sa valeur pour calculer chaque expression littérale :
| A = 7x – 3
Pour x = 5 |
B = x² + x – 9
Pour x = -2 |
C = -4x² – 2x + 2
Pour x = -3 |
| D = 2x – 7 + 3x + 1
Pour x = 4 |
E = (x – 3)²
Pour x = -4 |
F = (2x – 3)(6 – x²)
Pour x = 2 |
Exercice 34 :
- En utilisant l’identité « k(a + b) = ka + kb », développer les expressions suivantes :
| A = 7(x + 4) | B = 4(3 – 2x) | C = -3(x + 7) |
| D = -5(3x – 2) | E = -2x(5 + 4x) | F = 3x²(1 – 2x) |
- En utilisant l’identité « (a + b)(c + d) = ac + ad + bc + bd », développer les expressions suivantes :
| A = (x + 2)(x + 3) | B = (x – 7)(3x – 2) | C = (1 + 2x)(3 – x) |
| D = (-7x + 6)(5 – x²) | E = (3x + 4)(-x + 1) | F = (3x² – 4)(2x + 5) |
- Écrire le carré sous forme d’un produit puis développer les expressions suivantes :
| A = (x + 2)² | B = (1 + x)² | C = (2x + 1)² |
| D = (3 + 2x)² | E = (3x + 2)² | F = (x² + 5)² |
- Écrire le carré sous forme d’un produit puis développer les expressions suivantes :
| A = (x – 2)² | B = (x – 7)² | C = (2x + 5)² |
| D = (-4x + 3)² | E = (3x – 2)² | F = (x² – 3)² |
- En utilisant l’identité « (a + b)(c + d) = ac + ad + bc + bd », développer les expressions suivantes :
| A = (x + 2)(x – 3) | B = (x – 7)(x + 7) | C = (2x – 5)(2x + 5) |
| D = (3 – 4x)(3 + 4x) | E = (x² – 3x)(x² + 3x) | F = (2x² + 4)(2x² – 4) |
Exercice 35 :
En utilisant l’identité « ka + kb = k(a + b) », factoriser les expressions suivantes :
| A = 3x + 3y | B = 5x + 15 | C = 3 + 3a | |
| D = (2x + 1)(x + 4) + (2x + 1)(3x +2) | E = (x +7)² – (3x – 5)(x + 7) | ||
Télécharger ou imprimer cette fiche «calcul littéral : exercices de maths en 3ème corrigés en PDF.» au format PDF afin de pouvoir travailler en totale autonomie.
Réviser les cours et exercices avec nos Q.C.M :
D'autres ressources pour progresser en autonomie :
