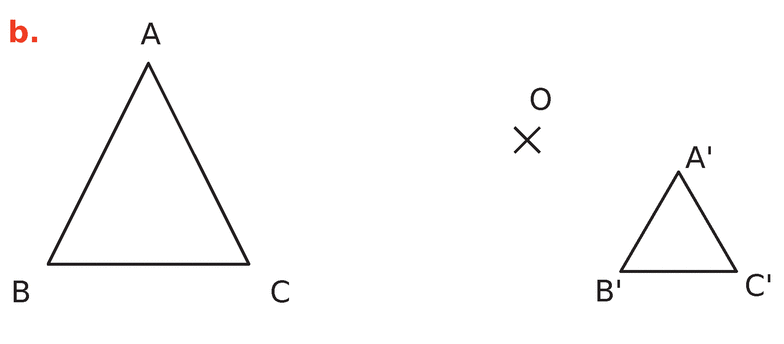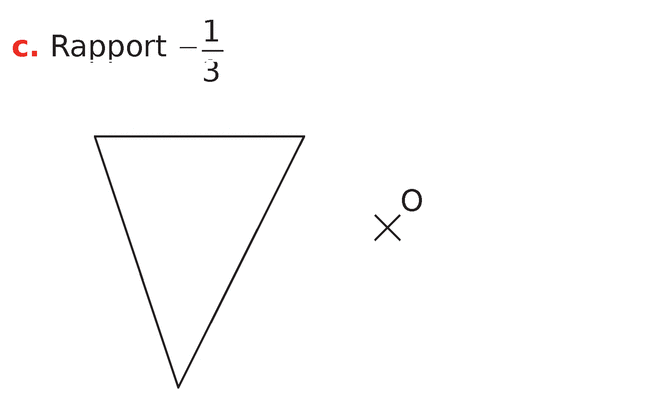Homothéties : exercices de maths en 3ème corrigés en PDF.

Les homothéties à travers des exercices de maths en 3ème corrigés en PDF. Nous étudierons la définition d’une homothétie de centre O et de rapport k. utilisation des différentes propriétés et construction de l’image d’une figure par une homothétie donnée. Nous retrouverons le théorème de Thalès ainsi que la notion de réduction, d’grandissement et de triangles semblables. Ces exercices en troisième disposent de leur correction ce qui permettra à l’élève de repérer ses erreurs afin de progresser en mathématiques et de développer des compétences.

Exercice 1 :
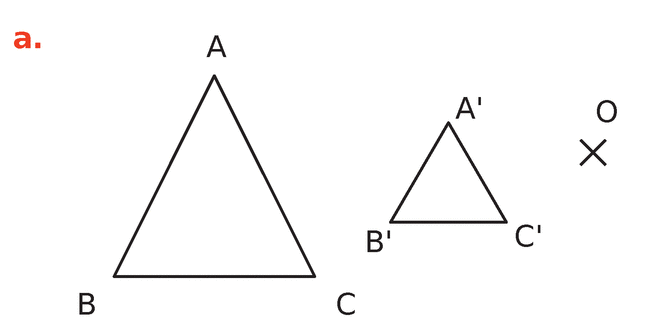
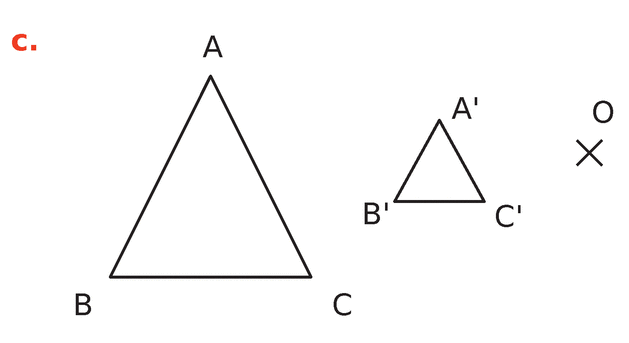
Dans chacun des cas suivants, dire si A’B’C’ est l’image du triangle ABC par une homothétie de
centre O.

Exercice 2 :

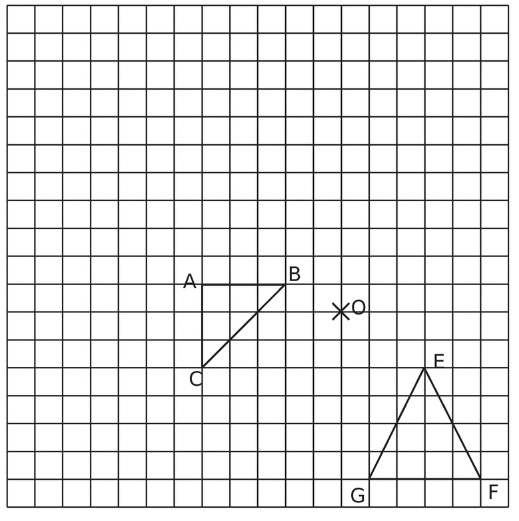
a. Construire A’B’C’, l’image par l’homothétie de centre O et de rapport 2 du triangle ABC
b. Construire E’F’G’, l’image par l’homothétie de centre O et de rapport du triangle EFG.

Exercice 3 :

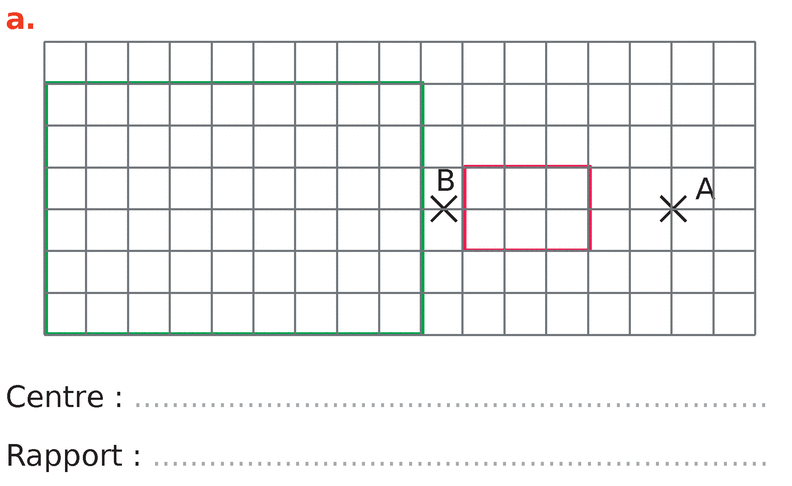
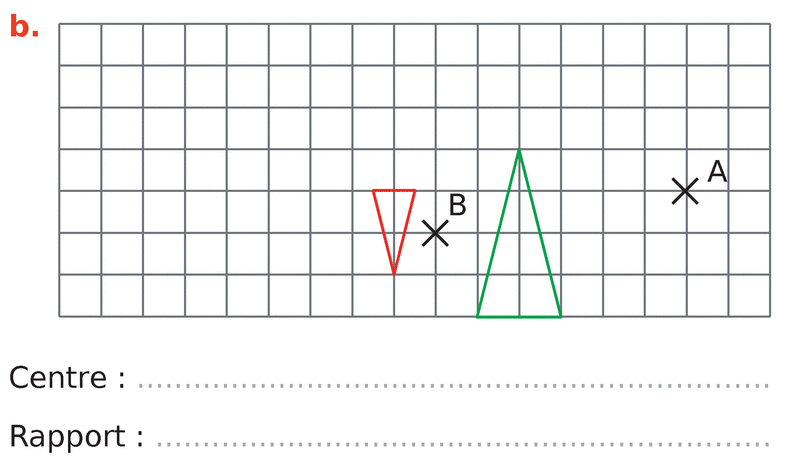
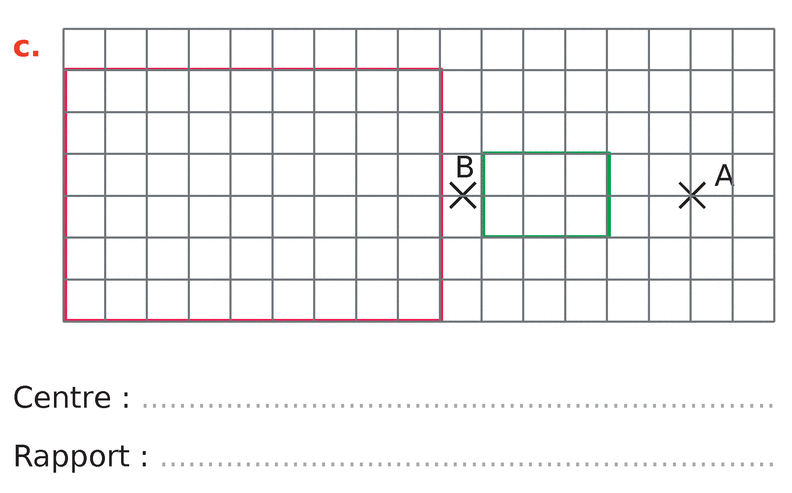
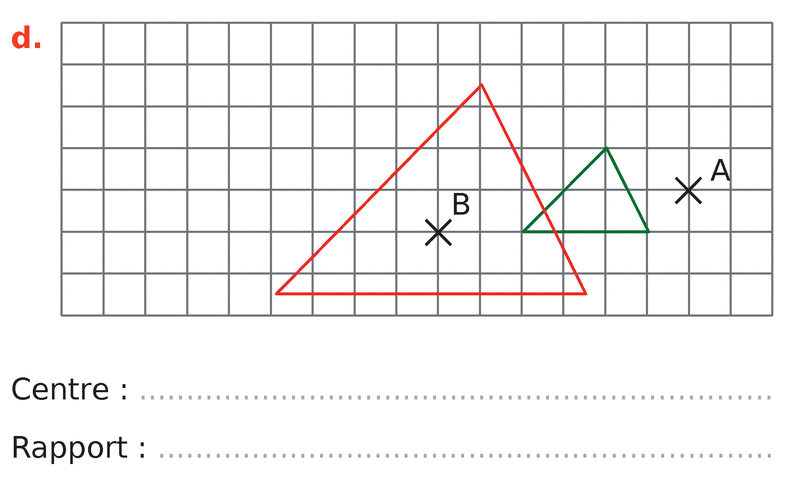
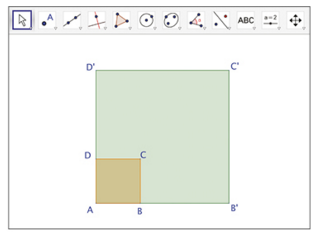
Dans chacun des cas suivants, la figure verte est l’image de la figure rouge par une homothétie.
Déterminer son centre et son rapport.

Exercice 4 :

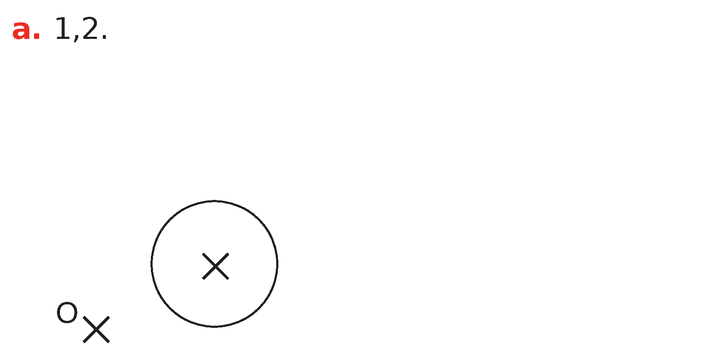
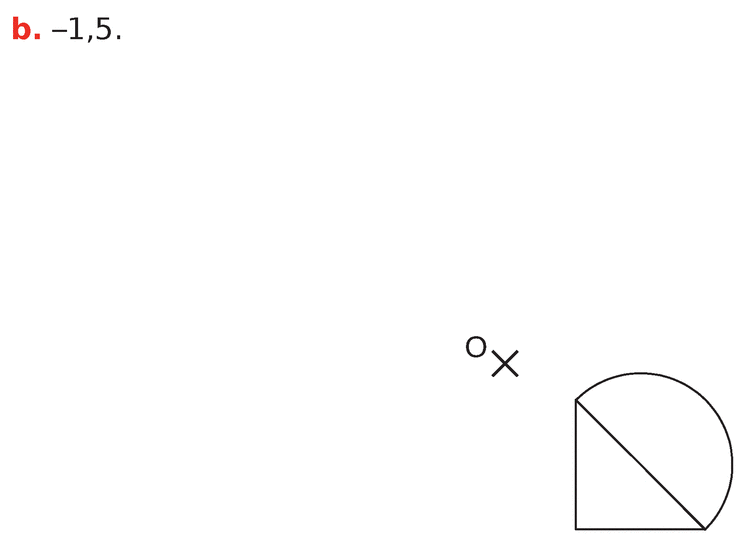
Dans chaque cas, construire l’image de la figure proposée par l’homothétie de centre O et de rapport
indiqué.

Exercice 5 :

Dans chaque cas, construire l’image de la figure dans l’homothétie de centre O et de rapport :

Exercice 6 :

L’homothétie de centre I et de rapport transforme un segment [AB] en un segment [A’B’].
a. Construire cette figure.
b. Que peut-on dire des droites (AB) et (A’B’) ?
Justifier.

Exercice 7 :

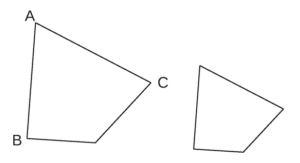
Les deux quadrilatères ci-dessous sont homothétiques.
a. Coder sur la figure les angles de même mesure.
b. Si AB = AC, coder sur la figure deux autres longueurs égales.
c. Repasser en rouge deux segments parallèles.

Exercice 8 :

Un triangle A’B’C’ est l’image d’un triangle ABC dans une homothétie de rapport $\frac{5}{4}$ .

On sait que AB = 6 cm et que l’angle $\widehat{ABC}$ mesure 60°.
Détermine les mesures de leurs images A’B’ et $\widehat{A'B'C'}$ . Justifier.

Exercice 9 :
RULP est un trapèze rectangle. OKFM est son image par une homothétie de rapport 0,5.
a. Construire le centre I de cette homothétie.

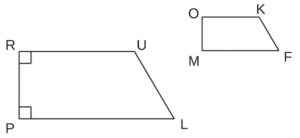
b. Quelle est la nature du quadrilatère OKFM ? Justifier.

Exercice 10 :

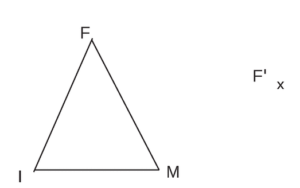
Terminer la construction de l’image du triangle FMI par une homothétie de rapport 0,5.

Exercice 11 :

Le carré EFGH est l’image du carré ABCD dans une homothétie de rapport 5.

On suppose que le côté du carré ABCD mesure 3 cm.

a. Calculer la mesure du côté de EFGH et en déduire son aire.

b. Compléter : Aire EFGH Aire ABCD $\frac{Aire\,EFGH}{Aire\,ABCD}=\frac{...}{...}=...=(...)^2$ .

Exercice 12 :

L’aire d’un pentagone est 24 cm².

Quelle sera l’aire de son image par une homothétie de rapport :
$a.\,0,8\,\,\,\,\,\,\,\,\,b.\,-\,4\,\,\,\,\,\,\,\,\,c.\,\frac{1}{7}$

Exercice 13 :

Compléter le tableau.

Exercice 14 :

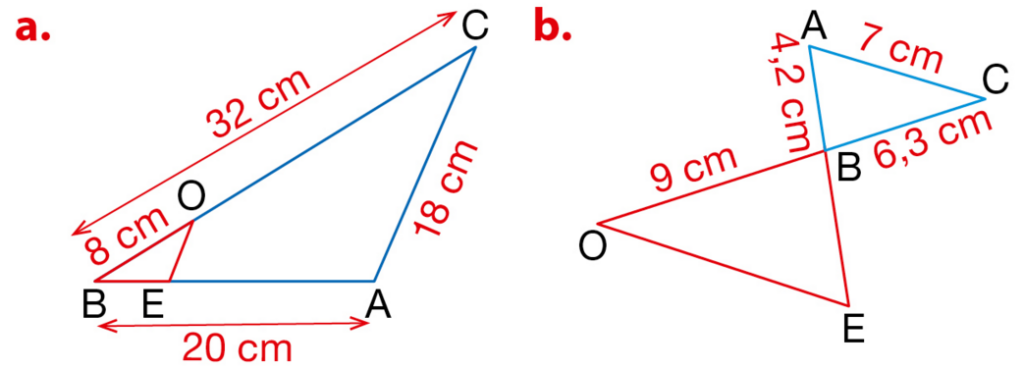
Dans chaque cas, on passe du triangle OBE au triangle ABC par une homothétie.
Donner le centre et le rapport de l’homothétie, puis calculer les longueurs OE et BE.

Exercice 15 :

a. Avec un logiciel de géométrie, construire un carré ABCD de côté 2 cm.
b. Construire l’image de ce carré par l’homothétie de centre A et de rapport 3.
Noter B’, C’, D’ les images respectives de B, C, D.
Quelle est la nature de AB’C’D ?
Quelle est la longueur de son côté ?

c. Construire l’image de ABCD par l’homothétie de centre A et de rapport $\frac{1}{4}$ .
Noter B », C », D » les images respectives de B, C, D.
Quelle est la nature de AB »C »D » ?
Quelle est la longueur de son côté ?
d. Construire l’image de ABCD par l’homothétie de centre A et de rapport $-\frac{1}{2}$ .
Noter les images respectives de B, C, D.
Quelle est la nature de AB »C »D » ?
Quelle est la longueur de son côté ?
e. Tracer les droites (AB), (AC), (AD). Que constate-t-on ?

Exercice 16 :

a. Construire un cercle $\varphi$ de centre O et de rayon 2 cm.
b. Par une homothétie, l’image d’un cercle est un cercle.
Construire l’image du cercle $\varphi$ par l’homothétie de centre O et de :

rapport 1,5
rapport 0,75
rapport -2.

Télécharger puis imprimer cette fiche en PDF.

Télécharger ou imprimer cette fiche «homothéties : exercices de maths en 3ème corrigés en PDF.» au format PDF afin de pouvoir travailler en totale autonomie.

Réviser les cours et exercices avec nos Q.C.M :

Q.C.M en 6ème Q.C.M en 5ème Q.C.M en 4ème Q.C.M en 3ème Q.C.M en 2de Q.C.M en 1ère Q.C.M en Terminale

D'autres ressources pour progresser en autonomie :

Chronomètre Horloge France Tables Multiplication Arrondir des décimaux Rapporteur et Angles Médiatrice Symétrie Axiale d'un triangle Symétrie Centrale d'un triangle Translation d'un triangle Rotation Homothétie Bissectrice Tracer droite parallèle Conversion Aires et Volumes Addition de deux relatifs Soustraction Relatifs Addition et soustraction de trois relatifs Produit Deux Relatifs Produit Trois Relatifs Quotient Relatifs Carré Entier Racine Carrée Théorème Pythagore Liste Diviseurs Décomposition Facteurs Premiers Calcul du PGCD PGCD Algorithme Euclide Test Nombre Premier Déterminer Fonction Linéaire Déterminer Fonction Affine Traceur Courbe Trigonométrie Angle Trigonométrie Longueur Périmètre d'un Cercle Aire d'un Disque Volume du Parallélépipède Rectangle Volume du cylindre Surface d'une Sphère et Volume d'une boule Volume d'une pyramide à base rectangulaire Section d'une pyramide Visualiser Section Cône en 2D Section d'un Cône Carte Mondiale Coordonnées Géographiques

Mathématiques Web c'est 2 250 077 fiches de cours et d'exercices téléchargées.