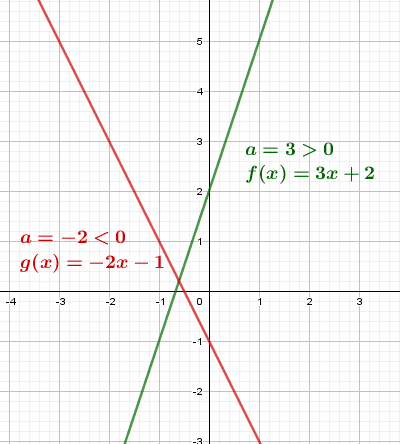Fonctions affines : cours de maths en 3ème à télécharger en PDF.

Sommaire de cette fiche

Les fonctions affines à travers un cours de maths en 3ème avec la définition, le vocabulaire et les différentes propriétés de ces fonctions est nécessaire pour la progression de l’élève. De plus, ce dernier doit être en mesure de faire l’étude de la courbe représentative et du sens de variation L’élève devra être capable de calculer une image ou un antécédent mais, également, savoir tracer la courbe d’une fonction affine à l’aide de deux points distincts. Aussi, il doit développer des compétences sur les fonctions affines en sachant déterminer la valeur du coefficient directeur a et de l’ordonnées à l’origine b. Nous terminerons cette leçon avec des exemples concrets issus de la vie courante en troisième.

I. Les fonctions affines : définition et vocabulaire.

Définition :

Soit « a » et « b » deux nombres fixés.En associant à chaque nombre « x » un nombre « ax + b» appelé « image de x »,

on définit une fonction affine.

On notera cette fonction ainsi : $g :x \mapsto ax + b$ .

L’image de x sera notée : g(x).

Exemple :

Soit g est la fonction affine définie par : $g : x \mapsto 2x-3$ .

alors :

l’image de 5 est : $g(5)= 2 \times 5- 3 = 10-3 = 7$ .
l’image de (-3) est : $g(-3) = 2 \times (-3) -3 = -6 - 3 = -9$ .
l’image de 0 est : $g(0) = 2 \times 0 - 3 = 0 - 3 = -3$ .

Remarque :

La fonction $f : x \mapsto 2x$ est la fonction linéaire associée à g.

Une fonction linéaire est affine, la réciproque est fausse.

Si b=0, nous obtenons la fonction linéaire associée $f:x \mapsto ax$ .

II. Représentation graphique d’une fonction affine

Propriété :

Soit g la fonction affine définie par : $g : x \mapsto ax + b$ .L’ensemble des points M de coordonnées est appelé représentation graphique de la fonction affine.

Dans un repère, cette représentation est la droite :

parallèle à la droite représentant la fonction linéaire associée.
passant par le point de coordonnées .

On dit que cette droite a pour équation : .

« a » est le coefficient directeur.
« b » est l’ordonnée à l’origine. Il indique la « hauteur » à laquelle la droite coupe l’axe des ordonnées.

Remarques :

– Si a = 0, la droite d’équation est parallèle à l’axe des abscisses.

– Toute droite non parallèle à l’axe des ordonnées admet une équation de la forme y = ax + b, et représente donc une fonction affine.

III. Sens de variation d’une fonction affine

Propriété :

Soient a et b deux nombres relatifs.

Soit g la fonction affine définie par $g:x \mapsto ax+b$ .

Si a>0 alors g est croissante.
Si a<0 alors g est décroissante.

Exemple :

Télécharger puis imprimer cette fiche en PDF.

Télécharger ou imprimer cette fiche «fonctions affines : cours de maths en 3ème en PDF.» au format PDF afin de pouvoir travailler en totale autonomie.

Vous devez vous inscrire ou vous connecter à votre compte afin de pouvoir télécharger ce document au format PDF.

D'autres cours et exercices à consulter

Mathématiques Web c'est 2 268 671 fiches de cours et d'exercices téléchargées.