Dérivée : exercices de maths en 1ère corrigés en PDF.

La dérivée d’une fonction numérique à travers des exercices de maths en 1ère corrigés qui ont été rédigés par un enseignant de l’éducation nationale.

Vous retrouverez dans ces énoncés les notions suivantes :

– limite du taux d’accroissement;
– dérivée et nombre dérivée en un point;
– dérivée d’une somme, d’un produit et d’un quotient;
– dérivée d’une fonction usuelle;
– tangente à une courbe et nombre dérivée.

L’élève devra savoir que la dérivée d’une fonction est une mesure du taux d’accroissement de cette fonction.

Elle est calculée en utilisant la formule suivante :

$f'(x)=\lim_{h\to\,0}\frac{f(x+h)-f(x)}{h}$

Savoir étudier la fonction dérivée et connaître les formulés de dérivation ainsi que savoir déterminer l’équation de la tangente en un point d’une courbe en déterminant la valeur du nombre dérivé. Ces énoncés sont accompagnés de leur correction pour vous permettre de repérer vos erreurs et augmenter vos notes en première.

Exercice 1 :

Déterminer sur quel ensemble est dérivable chacune des fonctions suivantes, puis déterminer sa dérivée.

a) $f:\,x\,\mapsto \,5x^2-\,3x+\,2$ définie sur $\mathbb{R}$ .

b) $g:x\,\mapsto \,100+\frac{1}{x}$ définie sur $\mathbb{R}^*$ .
c) $h:x\,\mapsto \,x\sqrt{x}$ définie sur $[0;+\infty[$ .

d) $j:x\,\mapsto \,\frac{12-5x}{9x+2}$ définie sur $\mathbb{R} - \{-\frac{2}{9} \}$ .

Exercice 2 :

Soit g la fonction définie sur $\mathbb{R}$ par $g:x\mapsto (-9x+ 1)^5$ .

Déterminer sur quel ensemble elle est dérivable puis déterminer sa dérivée.
Exercice 3 :

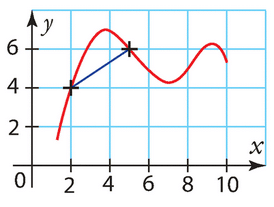
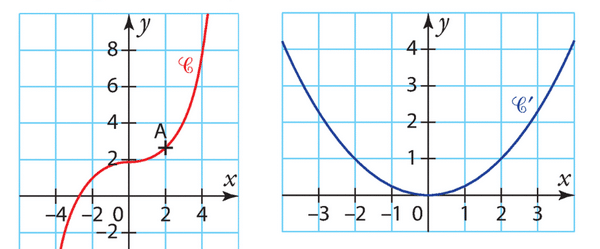
La fonction f est représentée par la courbe rouge ci-dessous.

Quel est le taux de variation de f entre 2 et 5 ?

Exercice 4 :

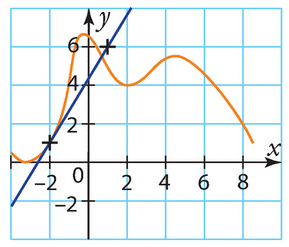
Sur le graphique ci-dessous la tangente en A(-2; 1) à la courbe

représentative d’une fonction f définie sur [-4 ; 9] passe par le point B(1 ; 6).
Déterminer f ‘ (-2).

Exercice 5 :

Soit f la fonction définie sur $[0;+\infty[$ par $f:x\,\mapsto \,\sqrt{x}-3$
et h un nombre réel non nul.
1. Montrer, à l’aide de l’identité remarquable
(a – b)(a + b) = a² – b², que le taux de variation de f entre 9 et 9 + h est égal à
$\frac{1}{\sqrt{9+h}+3}$ .

2. En déduire que la fonction est dérivable en 9 et déterminer f ‘ (9).
Exercice 6 :

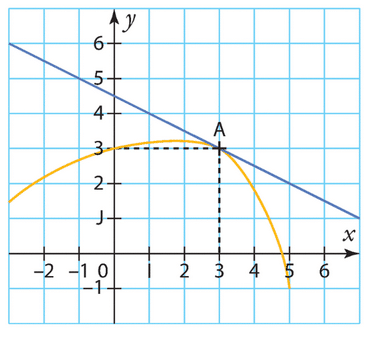
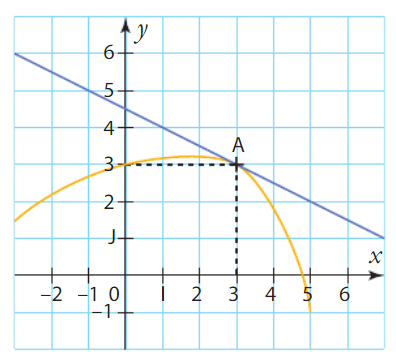
La courbe d’une fonction g définie sur [-3 ; 5] est représentée ci-dessous.

La tangente à cette courbe au point A d’abscisse 3 passe par le point de coordonnées (-3 ; 6).
Que vaut g(3) ? Que vaut g ‘ (3) ?

Exercice 7 :

Chacune des fonctions suivantes est de la forme d’une somme de deux fonctions u + v.

Dans chaque cas, identifier les fonctions u et v, et donner leurs ensembles de dérivabilité.

En déduire sur quel ensemble la fonction « somme » est dérivable,

puis déterminer l’expression de sa fonction dérivée.

$f:x\,\mapsto \,\frac{1}{x}+x$ $g:x\,\mapsto \,-5+\frac{1}{x^2}$ $h:x\,\mapsto \,x^4+x^2$

Exercice 8 :

Utiliser Geogebra pour répondre aux questions suivantes

portant sur la fonction $f:x\,\mapsto \,\frac{-9}{2x^2-4x+3}$ .

1. Saisir l’équation de la courbe représentative de f:
«y=-9/(22-4x+ 3)».

2. Placer un point sur la courbe.

3. Tracer la tangente à la courbe en ce point.

4. Afficher le coefficient directeur de la tangente.

5. En sélectionnant le point et en le plaçant à la bonne abscisse,

déterminer une valeur approchée de f ‘ (-2) ; f ‘ (-1); f ‘(0) ; f ‘ (1) et f ‘(2).

Exercice 9 :

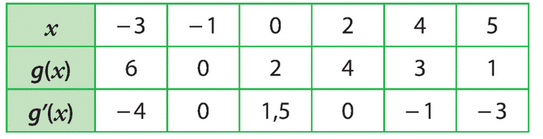
Soit g une fonction dérivable sur R. On a le tableau de valeurs suivant.

1. Dans un repère orthonormé placer les points de coordonnées (x; g(x)).

2. Construire en chacun de ces points les tangentes à la courbe représentative de la fonction g.

3. Représenter une allure possible de .
Exercice 10 :

On a représenté la courbe d’une fonction f en rouge et la courbe de sa fonction dérivée f ‘ en bleue.
Déterminer une valeur approchée du coefficient directeur de la tangente à 6 au point A d’abscisse 2.

Exercice 11 :

Déterminer pour chacune des fonctions suivantes, l’ensemble I sur lequel elle est dérivable,

puis sa fonction dérivée sur I.

$a)f(x)=\frac{5}{2x}+\frac{3}{4}-\frac{7x^2}{4}$ $b)g(x)=\frac{-4}{5x}(x-11)$

$c)h(x)=\frac{5x^2-8x+1}{21-7x}$ $d)j(x)=\frac{-5}{3x^2+2}$

$e)k(x)=\frac{9x}{x^2-6x+5}$ $f)m(x)=\sqrt{10-x}$

Exercice 12 :

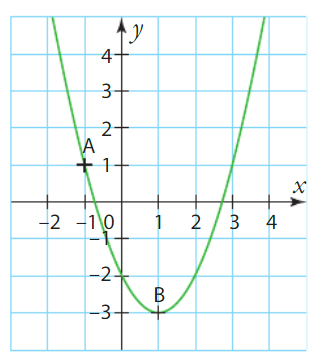
La courbe représentative d’une fonction f définie sur R passe par les points A et B.

Quel est le taux de variation de f entre —1 et 1 ?

Soit fla fonction définie sur $\mathbb{R}$ par $f:\,x\,\mapsto \,11x-\,7$ et h un nombre réel non nul.
Déterminer le taux de variation de f entre 3 et 3 + h.

Exercice 13 :

Soit f une fonction définie sur $\mathbb{R}$ et h un nombre réel non nul.
On sait que $\frac{f(-7+h)-f(-7)}{h}=\frac{5}{3}(4h+9)$ .
Peut-on dire que la fonction f est dérivable en -7 ? Si oui, déterminer $f'(-\,7).$

Exercice 14 :

Soit g une fonction définie sur $\mathbb{R}$ et x un nombre réel proche de 3 mais différent de 3.

On sait que $\frac{g(x)\,-\,g(3)}{x-3}=2x+3$ .
Peut-on dire que la fonction g est dérivable en 3 ? Si oui, déterminer g'(3).

Exercice 15 :

La courbe d’une fonction g définie sur [- 3 ; 5] est représentée ci-dessous.
La tangente à cette courbe au point A d’abscisse 3 passe par le point de coordonnées (- 3 ; 6).
Que vaut g(3) ? Que vaut g'(3) ?

Exercice 16 :

Soit f une fonction dérivable sur $\mathbb{R}$ telle que $f'(2)\,=-1$ et $f\,'(0)\,=\,2$ .

Soit C_f sa courbe représentative dans le repère ci-dessous.
Reproduire la courbe C_f (en plaçant quelques points importants et en respectant l’allure) et tracer la tangente à C_f au point d’abscisse 2 et la tangente à C_f au point d’abscisse 0.

Exercice 17 :

Pour chacune des fonctions suivantes, dire sur quel ensemble elle est dérivable, puis déterminer l’expression de sa fonction dérivée.
$f:x\,\mapsto \,x^4;\,g:x\,\mapsto \,x^{12};h:x\,\mapsto \,x^{-1};$

Chacune des fonctions suivantes est de la forme d’une somme de deux fonctions u + v.

Dans chaque cas, identifier les fonctions u et v, et donner leurs ensembles de dérivabilité.

En déduire sur quel ensemble la fonction « somme» est dérivable, puis déterminer l’expression de sa fonction dérivée.

$f:x\,\mapsto \,\frac{1}{x}+x\,;\,g:x\,\mapsto \,-5+\frac{1}{x^2};h:x\,\mapsto \,x^4+x^2;$

Exercice 18 :

Chacune des fonctions suivantes est de la forme d’un produit de deux fonctions $u\,\times \,v$ .

Dans chaque cas, identifier les fonctions u et v, et donner leurs ensembles de dérivabilité.
En déduire sur quel ensemble la fonction « produit » est dérivable, puis déterminer l’expression de sa fonction dérivée.

$f:x\,\mapsto \frac{1}{x}(9-6x);\,g:x\,\mapsto \,x^2\sqrt{x};h:x\,\mapsto \,(x^5+x^3)(x^2-4);$

Exercice 19 :

Soit f la fonction définie sur $I=]-4;+\infty[$ par $f:x\,\mapsto \,\frac{1}{2x+8}$ .

1.f est de la forme $\frac{1}{v}$ .
Donner l’expression de la fonction v et résoudre l’équation v(x)=0.

2. En utilisant le théorème de la dérivée de l’inverse d’une fonction, démontrer que la fonction f est dérivable sur I et donner l’expression de sa dérivée .

Exercice 20 :

Soit h la fonction définie sur $I=]-4;+\infty[$ par $h:x\,\mapsto \,\sqrt{-3x+12}$ .
1. h est une fonction composée de deux fonctions g et f dans cet ordre.
Donner l’expression des fonctions g et f.
2. En utilisant le théorème de la dérivée d’une fonction composée, démontrer que la fonction h est dérivable sur l.
3. Déterminer l’expression de f'(x) pour tout réel strictement positif x et celle de g'(x) pour tout réel x de I.
4. En déduire l’expression de la dérivée .

Exercice 21 :

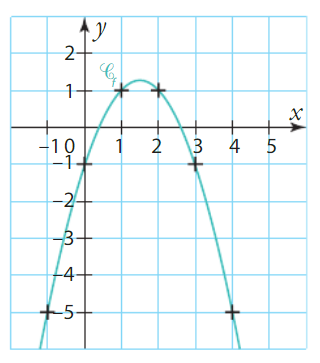
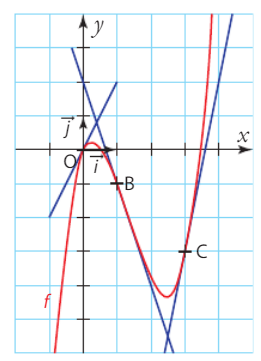
Dans le repère orthonormé (O ; i, J) ci-dessous, la courbe rouge C_f représente une
fonction f définie et dérivable sur $\mathbb{R}$ , les droites tracées en bleu représentent les
tangentes à C_f respectivement au point O, au point B d’abscisse 1 et au point C d’abscisse
3.

1. Déterminer graphiquement f'(0) , f'(l) et $f\,'(3).$
2. Déterminer l’équation réduite de la tangente à C_f au point C.
3. La courbe C_f est la représentation graphique de la fonction $f:\,x\,\mapsto \,x^3-4x^2\,+2x$ .
Retrouver par le calcul les résultats des questions 1. et 2.

Voir Exercices 11 à 21...

Télécharger puis imprimer cette fiche en PDF.

Télécharger ou imprimer cette fiche «dérivée : exercices de maths en 1ère corrigés en PDF.» au format PDF afin de pouvoir travailler en totale autonomie.

Réviser les cours et exercices avec nos Q.C.M :

Q.C.M en 6ème Q.C.M en 5ème Q.C.M en 4ème Q.C.M en 3ème Q.C.M en 2de Q.C.M en 1ère Q.C.M en Terminale

D'autres ressources pour progresser en autonomie :

Chronomètre Horloge France Tables Multiplication Arrondir des décimaux Rapporteur et Angles Médiatrice Symétrie Axiale d'un triangle Symétrie Centrale d'un triangle Translation d'un triangle Rotation Homothétie Bissectrice Tracer droite parallèle Conversion Aires et Volumes Addition de deux relatifs Soustraction Relatifs Addition et soustraction de trois relatifs Produit Deux Relatifs Produit Trois Relatifs Quotient Relatifs Carré Entier Racine Carrée Théorème Pythagore Liste Diviseurs Décomposition Facteurs Premiers Calcul du PGCD PGCD Algorithme Euclide Test Nombre Premier Déterminer Fonction Linéaire Déterminer Fonction Affine Traceur Courbe Trigonométrie Angle Trigonométrie Longueur Périmètre d'un Cercle Aire d'un Disque Volume du Parallélépipède Rectangle Volume du cylindre Surface d'une Sphère et Volume d'une boule Volume d'une pyramide à base rectangulaire Section d'une pyramide Visualiser Section Cône en 2D Section d'un Cône Carte Mondiale Coordonnées Géographiques

Mathématiques Web c'est 2 251 060 fiches de cours et d'exercices téléchargées.