L’arithmétique avec des exercices de maths en 3ème corrigés sont toujours à considérer. Ainsi, la notion de multiple et de diviseurs d’un nombre entier est très important. De plus, avec ce chapitre, vous saurez effectuer la décomposition en facteurs premiers de n’importe quel entier positif. L’élève devra connaître la définition d’un nombre premier puis, également, savoir déterminer la valeur du plus grand commun diviseur (PGCD) de deux entiers. Nous terminerons cette série d’énoncés corrigés par des problèmes concrets de la vie courante qui sont similaires à ceux disponibles dans votre manuel scolaire en troisième.
Exercice 1 :
Écrire sous forme de fraction irréductible le nombre .
Indication : on pourra donner la décomposition en facteurs premiers des nombres 325 et 1 053 puis calculer le PGCD des nombres 1 053 et 325.
Exercice 2 :
1.Donner la décomposition en facteurs premiers des nombres 630 et 924.
2.Ecrire sous forme irréductible la fraction en donnant le détail de tous les calculs.
Exercice 3 :
Un philatéliste possède 1 631 timbres français et 932 timbres étrangers. Il souhaite vendre toute sa collection en réalisant des lots identiques, c’est à dire comportant le même nombre de timbres et la même répartition de timbres français et étrangers
1. Calculer le nombre maximum de lots qu’il pourra réaliser.
2. Combien y aura-t-il, dans ce cas, de timbres français et étrangers par lot ?
Exercice 4 :
1/ Déterminer le PGCD des nombres 108 et 135.
2/ Marc à 108 billes rouges et 135 noires. Il veut faire des paquets de sorte que :
– Tous les paquets contiennent le même nombre de billes rouges ;
– Tous les paquets contiennent le même nombre de billes noires ;
– Toutes les billes rouges et toutes les billes noires sont utilisées.
a. Quel nombre maximal de paquets pourra-il réaliser ?
b. Combien y aura-t-il de billes rouges et de billes noires dans chaque paquet ?
Exercice 5 :
1.Donner la décomposition en facteurs premiers des nombres 325 et 1053.
2.Écrire sous forme de fraction irréductible le nombre
Exercice 6 :
1.Déterminer la décomposition en facteurs premiers de 110 et 88.
2.Calculer le PGCD de 110 et 88.
3.Un ouvrier dispose de plaques de métal de 110 cm de longueur et de 88 cm de largeur. Il a reçu la consigne suivante : « Découper dans ces plaques des carrés tous identiques, les plus grands possibles, de façon à ne pas avoir de perte ».
Quelle sera la longueur du côté d’un carré ?
4.Combien obtiendra-t-il de carrés par plaques ?
Exercice 7 :
Pour le 1er Mai, Julie dispose de 182 brins de muguet et 78 roses.
Elle veut faire le plus grand nombre de bouquets identiques en utilisant toutes les fleurs.
Combien de bouquets identiques pourra-t-elle faire ?
Quelle sera la composition de chaque bouquet ?
Exercice 8 :
Un chocolatier vient de fabriquer 2 622 œufs de Pâques et 2 530 poissons en chocolat.
Il souhaite vendre des assortiments d’œufs et de poissons de façon que :
® tous les paquets aient la même composition.
® après mise en paquet, il reste ni œufs, ni poissons.
1) Aider ce chocolatier à choisir la composition de chaque paquet : donner toutes les possibilités.
2) Quel est le plus nombre de paquets qu’il peut réaliser ?
Exercice 9 :
On répartit en paquets un lot de 161 crayons rouges et un lot de 133 crayons noirs de façon que tous les crayons d’un paquet soient de la même couleur et que tous les paquets contiennent le même nombre de crayons.
a) Combien y a-t-il de crayons dans chaque paquet ?
b) Quel est le nombre de paquets de crayons de chaque couleur ?
Exercice 10 :
Une boite de jeux de société a la forme d’un parallélépipède rectangle. Les arêtes mesurent un nombre entier de centimètres ; les faces ont pour aire 96 cm², 160 cm² et 240 cm².
Quel est le volume de la boite ?
Exercice 11 :
Une malle a la forme d’un parallélépipède rectangle de dimensions 140 cm, 112 cm et 84 cm. On veut la remplir de cubes identiques dont l’arête mesure un nombre entier de centimètres.
1) Calculer l’arête du plus grand cube possible.
2) Calculer les arêtes des autres cubes qui pourraient remplir la malle.
3) Calculer dans chaque cas le nombre de cubes nécessaires pour remplir la malle.
Exercice 12 :
Les côtés d’un terrain triangulaire mesurent 198 m, 254 m et 306 m.
On plante des arbres le long des côtés, également espacés, avec un arbre à chaque sommet. La distance qui sépare deux arbres consécutifs est mesurée par un nombre entier de mètres.
Quel le nombre minimum d’arbres qu’il faut acheter ?
Exercice 13 :
Deux bus A et B partent en même temps du terminus 7 h.
Le bus A part toutes les 36 min du terminus alors que le bus B part toutes les 24 min.
A quelle heure les deux bus partiront de nouveau en même temps :
a. pour la première fois ?
b. pour la deuxième fois ?
c. pour la cinquième fois ?
Exercice 14 :
Dans la liste suivante, un seul nombre est un nombre premier. Lequel ?
Exercice 15 :
Alan possède un nombre premier de macarons.
Pourra-t-il les partager avec ses amis de manière équitable ?
Expliquer.
Exercice 16 :
Patricia place ses 24 pions sur une grille de façon à former le plus grand nombre de rectangles
de dimensions différentes.
En voici un exemple. On compte ces deux rangements comme une seule possibilité.
a. Trouver toutes les possibilités de Patricia pour placer ainsi ses 24 pions.
b. Léo affirme : « Avec le nombre de pions que je possède, je n’ai qu’une possibilité. »
Que peut-on en déduire pour le nombre de pions de Léo ?
Exercice 17 :
Nadia a remarqué que 256 = 16 x 16.
A l’aide de cette remarque, écrire la décomposition en produit de facteurs premiers du nombre 256.
Exercice 18 :
Une boîte contient 150 bonbons au chocolat noir et 120 au chocolat blanc.
a. Donner sous forme d’une fraction irréductible la proportion de bonbons au
chocolat noir dans la botte.
b. Hugo mange 3 bonbons au chocolat noir et 3 bonbons au chocolat blanc.
A-t-on encore la même proportion de bonbons au chocolat noir dans la boîte ?
Exercice 19 :
Grâce un algorithme trouvé sur Internet, Paul a obtenu les résultats suivants :
•
•
Lors d’un match de rugby, le stade comptait 59 535 spectateurs dont 33 291 supporters de l’équipe
française.
Donner la fraction irréductible représentant la proportion de supporters de l’équipe française.
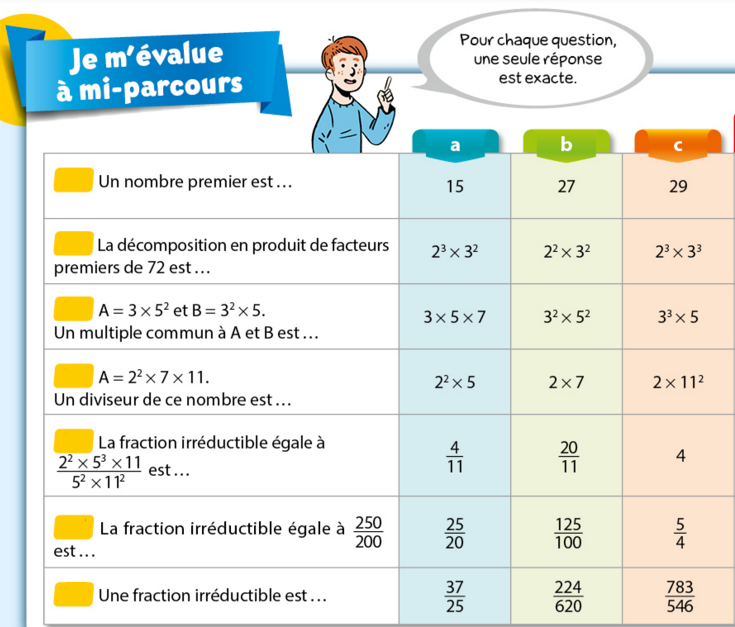
Exercice 20 :
Effectuer le QCM sur l’arithmétique et la décomposition en facteurs premiers suivant :
Télécharger puis imprimer cette fiche en PDF.
Télécharger ou imprimer cette fiche «arithmétique et décomposition en facteurs premiers : exercices de maths en 3ème corrigés en PDF.» au format PDF afin de pouvoir travailler en totale autonomie.
D'autres cours et exercices à consulter
- Théorème de Thalès : exercices de maths en 3ème corrigés en PDF.
- Fonctions : exercices de maths en 3ème corrigés en PDF.
- Trigonométrie : exercices de maths en 3ème corrigés en PDF.
- Homothéties : exercices de maths en 3ème corrigés en PDF.
- Les équations : exercices de maths en 3ème corrigés en PDF.
- Probabilités : exercices de maths en 3ème corrigés en PDF.
- Fonctions linéaires : exercices de maths en 3ème corrigés en PDF.
- Calcul littéral : exercices de maths en 3ème corrigés en PDF.