Les volumes et sections et les sections de solides sur la géométrie dans l’espace avec des exercices de maths en 3ème corrigés afin de vous permettre de vous exercer en ligne.
Ces énoncés font intervenir les notions suivantes :
- les différents volumes : boule, pyramide, cône de révolution, prisme droit;
- formule de calcul de volumes;
- sections de volumes dans l’e
- réduction et agrandissement.
Ces énoncés corrigés sont à télécharger gratuitement au format PDF.
Exercice 1 :
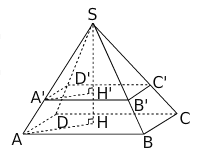
On réalise la section d’une pyramide SABCD à base rectangulaire par un plan parallèle
à sa base à 5 cm du sommet.
Nous avons AB=4,8 cm; BC = 4,2 cm et SH = 8 cm.
- Calculer le volume de la pyramide SABCD.
- La pyramide SA’B’C’D’ est une réduction de la pyramide SABCD.
- Donner le rapport de cette réduction.
- En déduire le volume de la pyramide SA’B’C’D’.
Exercice 2 :
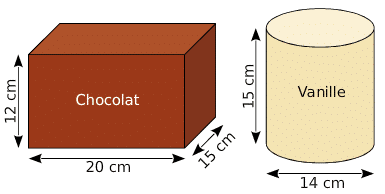
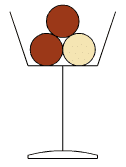
Un restaurant propose en dessert des coupes de glace composées de trois boules
supposées parfaitement sphériques, de diamètre 4,2 cm.
Le pot de glace au chocolat ayant la forme d’un parallélépipède rectangle est plein,
ainsi que le pot de glace cylindrique à la vanille.
Le restaurateur veut constituer des coupes avec deux boules au chocolat et une boule à la vanille.
- Montrer que le volume d’un pot de glace au chocolat est de 3 600
.
2.Calculer la valeur arrondie au du volume d’un pot de glace à la vanille.
3.Calculer la valeur arrondie au du volume d’une boule contenue dans la coupe.
4.Sachant que le restaurateur doit faire 100 coupes de glace, combien doit-il acheter
de pots au chocolat et de pots à la vanille ?
Exercice 3 :
Une pyramide régulière de sommet S et de hauteur SO = 9 cm a pour
base un carré ABCD de côté 4,5 cm.
Elle est coupée par un plan parallèle à sa base qui coupe sa hauteur en O, tel que SO’ = 6 cm.
a. Quelle est la nature de la section A’B’C’D’?
b. Calculer le volume de la pyramide réduite SA’B’C’D’.
Exercice 4 :
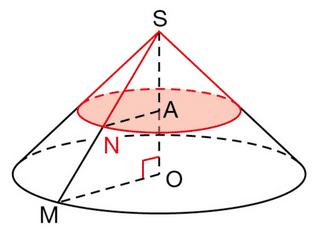
Un cône de hauteur SO = 18 cm a pour base un disque de rayon 15 cm.
A est le point de la hauteur [SO] tel que SA=10 cm.
Le plan passant par A et parallèle à la base coupe le segment [SM] en N.
Calculer le volume, en , du cône réduit de sommet S et de base le disque de centre A et de rayon AN.
Donner une valeur approchée à l’unité près.
Exercice 5 :
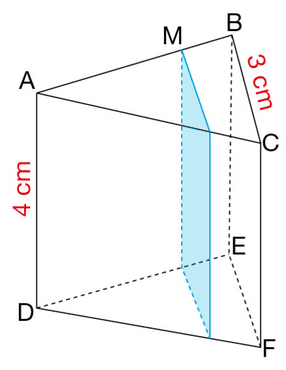
Le rectangle bleu est la section du prisme droit ABCDEF par un plan parallèle à la face BCFE et
passant par un point M de l’arête [AB].
Donner la nature et la (ou les) dimension(s) de cette section :
a. lorsque M est en A,
b. lorsque M est en B,
c. lorsque M est le milieu de [AB].
Exercice 6 :
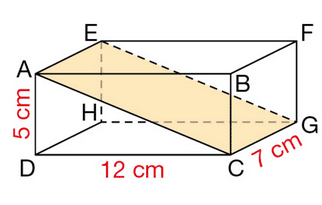
En coupant ce parallélépipède rectangle par le plan passant par A et C et parallèle à l’arête [DH],
on obtient la section AEGC.
a. Quelle est sa nature ?
b. Dessiner cette section en vraie grandeur.
c. Calculer la longueur AC, en cm.
Exercice 7 :
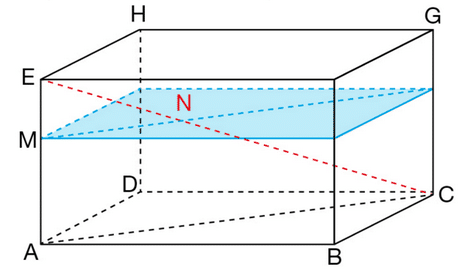
ABCDEFGH est un parallélépipède rectangle tel que AB = 12 cm, AD=5 cm, AE=8 cm.
Le point M de [AE] est tel que AM =6 cm.
La section de ce solide par un plan parallèle à la face ABCD et passant par M est représentée en bleu.
a. Utiliser le théorème de Pythagore pour calculer AC.
b. Utiliser le théorème de Thalès pour calculer MN.
Exercice 8 :
Pour créer une lampe de décoration, une machine tranche un cylindre métallique selon les
données indiquées.
Calculer la valeur exacte de MN.
Exercice 9 :
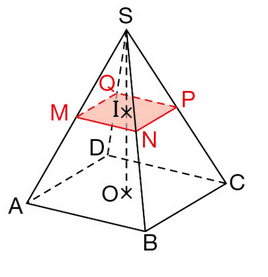
SABCD est une pyramide régulière à base carrée de côté 6 cm et de hauteur P
[SO] avec SO = 7,5 cm.
Un plan parallèle à la base coupe [SO] en I de sorte que SI=2,5 cm.
La section est le quadrilatère MNPQ.
a. Calculer le volume , en , de SABCD.
b. est le volume, en , de SMNPQ.
Exprimer en fonction de .
Donner une valeur approchée de au centième près.
Exercice 10 :
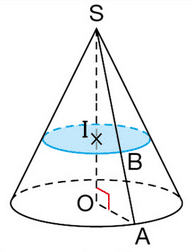
Un cône de révolution de sommet S et de base un disque de centre O est coupé par un plan
parallèle à sa base.
La section est le cercle de centre I qui passe par B, point d’intersection du segment [SA] avec le plan.
a. Le cône de sommet S et dont la base est le disque de centre I passant par B est une réduction du cône .
Écrire le rapport de réduction de trois façons différentes.
b. On donne SO =10 cm, 0A=7,5 cm et SI=6 cm.
Dessiner la section en vraie grandeur.
Exercice 11 :
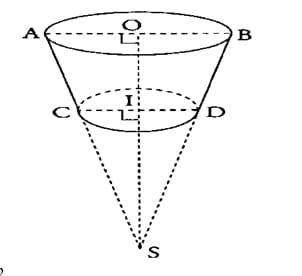
Un panier a la forme d’un tronc de cône dont les bases ont pour diamètres les segments [AB] et [CD], situés dans un même plan.
Le petit cône de sommet S et de disque de base de rayon [ICl est une réduction du grand cône de sommet S et de disque de base de rayon [OA].
Il est inutile de reproduire la figure ci-dessus, représentant un tronc de cône.
On donne : AB=30cm CD = 20 cm
1. a) Démontrer, à partir des indications portées sur la figure, que les droites (AO) et (CI) sont parallèles.
b) Démontrer que .
2.a) Calculer le volume V2 du petit cône en fonction du volume V1 du grand cône.
b) Montrer que le volume V du tronc de cône est :
.
Exercice 12 :
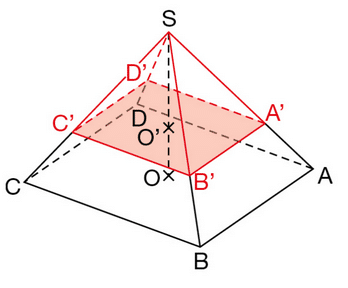
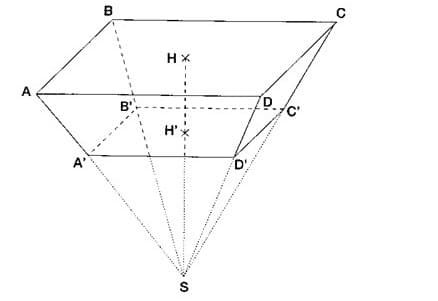
Une boîte de chocolats a la forme d’une pyramide tronquée (figure ci-dessous).
Le rectangle ABCD de centre H et le rectangle A’B’C’D’ de centre H’ sont dans des plans parallèles.
On donne :
AB = 6 cm
BC = 18 cm
HH’ = 8 cm
SH = 24 cm
1) Calculer le volume V1 de la pyramide SABCD de hauteur SH.
2) Quel est le coefficient k de la réduction qui permet de passer de la pyramide SABCD à la pyramide SA’B’C’D’ de hauteur SH’ ?
3) En déduire le volume V2 de la pyramide SA’B’C’D’ puis le volume V3 de la boîte de chocolats ?
Exercice 13 :
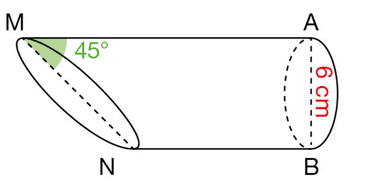
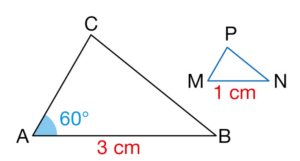
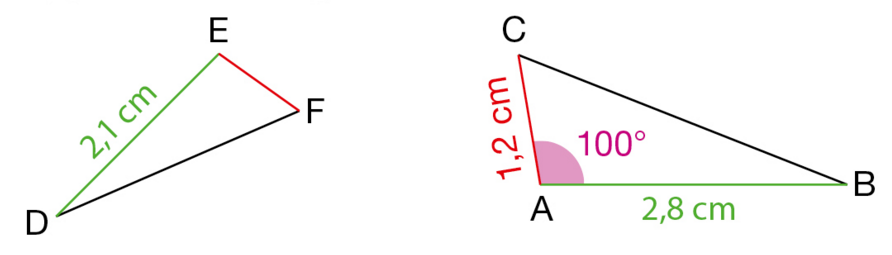
Le triangle MNP est une réduction du triangle ABC.
Dans quel rapport ?
En déduire la mesure de l’angle .
Exercice 14 :
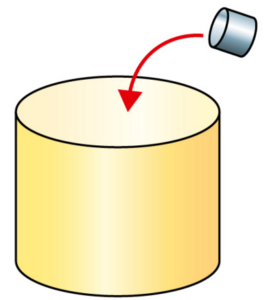
On veut remplir un récipient en forme de cylindre à l’aide d’un récipient de même
forme dont les dimensions sont 5 fois plus petites.
Combien de fois devra-t-on verser tout le contenu du petit dans le grand ?
Exercice 15 :
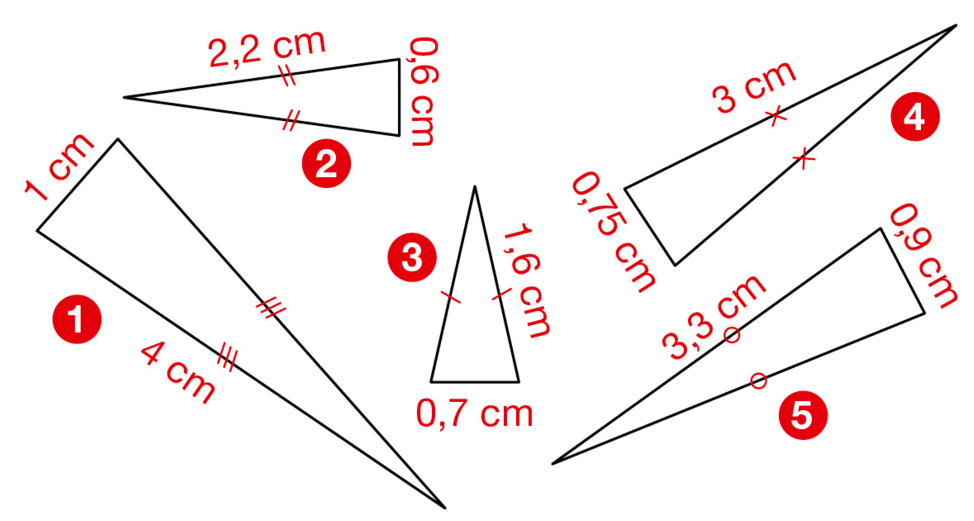
Associer les triangles qui sont un agrandissement ou une réduction l’un de l’autre.
Exercice 16 :
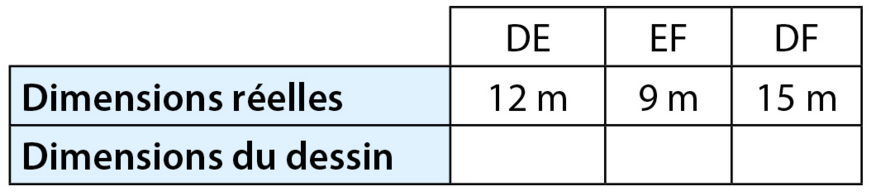
On veut représenter à l’échelle ce parc de jeux triangulaire dont les dimensions
sont indiquées sur cette figure à main levée.
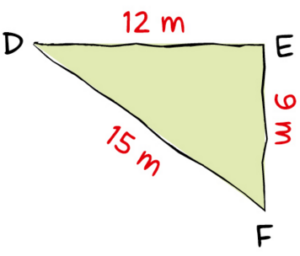
Donner les longueurs DE, EF et DF ci-dessous :
Exercice 17 :
Le triangle DEF est une réduction dans le rapport k du triangle ABC.
a. Calculer le rapport k de réduction.
b. Calculer la longueur du segment [EF].
c. Donner la mesure de l’angle .
2. Le triangle ABC est un agrandissement de rapport k’ du triangle DEF.
Donner la valeur exacte de k’.
Exercice 18 :
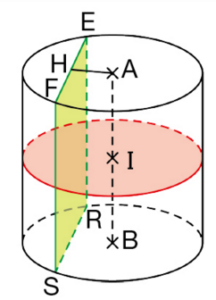
On a coupé par deux plans ce cylindre dont les bases sont deux disques de centres A et B ; les
sections sont représentées l’une en rose, l’autre en vert.
H est le milieu de [EF] et :
AH = 3 cm, AB = 8 cm, AE = 5 cm.
1. Donner la description de chacun des deux plans.
2. Construire en vraie grandeur :
a. la section rose ;
b. le triangle AEF puis la section verte.
3. a. Calculer EF.
b. Vérifier cette longueur sur le dessin en vraie grandeur.
Exercice 19 :
Télécharger ou imprimer cette fiche «volumes et sections : exercices de maths en 3ème corrigés en PDF.» au format PDF afin de pouvoir travailler en totale autonomie.
Réviser les cours et exercices avec nos Q.C.M :
D'autres ressources pour progresser en autonomie :
