La trigonométrie à travers un cours de maths en 3ème sur le cosinus, sinus et la tangente d’un angle aigu et le calcul de la mesure d’un angle dans un triangle rectangle en 3ème est très instructif. Nous verrons dans cette leçon comment calculer la longueur d’un côté d’un triangle rectangle connaissant son cosinus, sinus ou sa tangente. Puis, nous calculerons la mesure d’un des angles aigus d’un triangle rectangle connaissant deux de ses longueurs ainsi que l’utilisation de la calculatrice avec le mode degré (DEG).
I. Cosinus, sinus et tangente :
1.Définitions :
Définition :
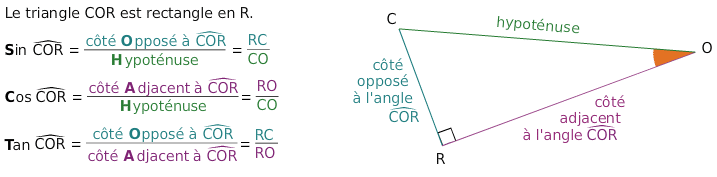
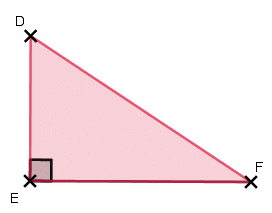
On considère un triangle rectangle et ses angles aigus.
Le cosinus d’un angle aigu est égal au quotient du côté adjacent à l’angle et de l’hypoténuse du triangle rectangle.
Le sinus d’un angle aigu est égal au quotient du côté opposé à l’angle et de l’hypoténuse du triangle rectangle.
Le tangente d’un angle aigu est égal au quotient du côté opposé à l’angle et du côté adjacent à l’angle.
Exemple :
Remarque :
Pour retenir facilement ces formules, on peut utiliser le moyen mnémotechnique suivant :SOH-CAH-TOA qui correspond aux initiales en gras dans les formules précédentes.
Le cosinus et le sinus d’un angle aigu sont toujours compris entre 0 et 1.
La tangente d’un angle aigu est un nombre strictement positif.
2.Applications :
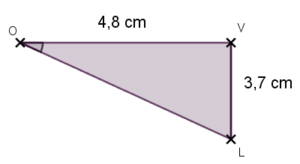
Exemple :
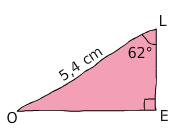
Dans le triangle rectangle LOE, Calculer OE.
On connait :
l’angle ;
la longueur OL (hypoténuse)
On cherche :
la longueur OE (opposé)
Formule :
La seule formule qui fait apparaître les mots « hypoténuse » et « opposé » est le sinus.
En utilisant la propriété du produit en croix :
II. Calcul de la mesure d’un angle :
Méthode :
Pour calculer la mesure d’un angle, on prend le soin de vérifier que sa calculatrice est en mode DEGRE.
On utilise les touches arccos, arcsin, arctan.
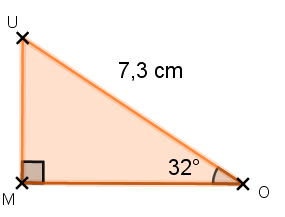
Exemple :
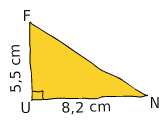
Dans le triangle rectangle FUN, déterminer la mesure de l’angle arrondie au degré.
Dans ce triangle rectangle,
on connaît :
la longueur UN (adjacent);
la longueur FU (opposé).
La seule formule qui fait apparaître les mots « adjacent » et « opposé » est la tangente.
On utilise la calculatrice en mode DEGRE et la touche « arctan ».
.
Avez-vous assimilé ce cours sur la trigonométrie dans le triangle rectangle en 3ème ?
La trigonométrie dans le triangle rectangle
Limite de temps: 0
Résumé-Quiz
0 questions correctes sur 10
Questions:
1
2
3
4
5
6
7
8
9
10
Information
Un QCM sur la trigonométrie dans le triangle rectangle.
Vous avez déjà rempli le questionnaire avant. Par conséquent, vous ne pouvez pas recommencer.
Quiz is loading...
You must sign in or sign up to start the quiz.
Vous devez finir le quiz suivant, avant de commencer celui-ci :
Résultats
0 questions sur 10 répondues correctement
Votre temps:
Temps écoulé
Vous avez atteint 0 points sur 0 , (0)
Score moyen
Votre score
Categories
Not categorized0%
1
2
3
4
5
6
7
8
9
10
Répondu
Examiner
Question 1 sur 10
Quelle est la formule du cosinus d’un angle aigu dans un triangle rectangle ?
Exact
Inexact
Question 2 sur 10
Quelle est la formule du sinus d’un angle aigu dans un triangle rectangle ?
Exact
Inexact
Question 3 sur 10
Quelle est la formule de la tangente d’un angle aigu dans un triangle rectangle ?
Exact
Inexact
Question 4 sur 10
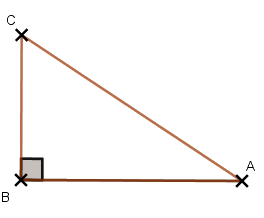
Dans ce triangle ABC, quelle est l’expression de
Exact
Inexact
Question 5 sur 10
Dans ce triangle DEF, quelle est l’expression de
Exact
Inexact
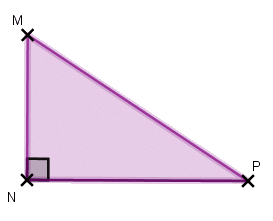
Question 6 sur 10
Dans ce triangle MNP, quelle est l’expression de
Exact
Inexact
Question 7 sur 10
Parmi ces différentes formules, quelles sont celles qui sont correctes ?
Exact
Inexact
Question 8 sur 10
Parmi ces résultats, lesquels sont impossibles ?
Exact
Inexact
Question 9 sur 10
Dans ce triangle MUO, nous avons :
Exact
Inexact
Question 10 sur 10
Dans ce triangle OVL, nous avons :
Exact
Inexact
Télécharger puis imprimer cette fiche en PDF.
Télécharger ou imprimer cette fiche «trigonométrie : cours de maths en 3ème en PDF.» au format PDF afin de pouvoir travailler en totale autonomie.
Vous devez vous inscrire ou vous connecter à votre compte afin de pouvoir télécharger ce document au format PDF.
;
