Fonctions : exercices de maths en 3ème corrigés en PDF.

Généralités sur les fonctions numériques avec des exercices de maths en 3ème corrigés. L’élève devra connaître la définition d’une fonction et savoir calculer une image ou déterminer l’antécédent d’un nombre. Exploiter la représentation graphique afin de déterminer des images ou des antécédents. Développer des compétences sur les fonctions numériques avec la correction qui permet aux élèves de repérer leurs erreurs et par conséquent, combler leurs lacunes et progresser en troisième.

Exercice 1 :

Traduire à l’aide d’écritures simples les phrases suivantes (et réciproquement..) :

a. f(2) = 4

b. La courbe de la fonction f passe par le point A(4 ; −1).

c. L’ordonnée du point d’abscisse 4 de la courbe C de g vaut 2.

d. La représentation graphique de la fonction h coupe l’axe des ordonnées au point d’ordonnée 3.

e. La courbe représentant la fonction k passe par l’origine.

f. La courbe C représentant la fonction g est au-dessus de l’axe des abscisses entre les points

d’abscisse −4 et 1.

Exercice 2 :

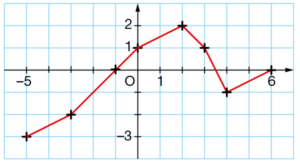
Dans le repère ci-dessous, on note f la fonction représentée par son graphe.

Vérifier, en plaçant le point P (-7 ; -3) dans le repère, que celui-ci appartient bien à la courbe. Compléter alors la colonne du tableau ci-dessous correspondant à ce point.
Placer dans le repère le point Q appartenant à la courbe sachant que son abscisse est -2. Compléter la colonne du tableau correspondant à ce point.
Placer dans le repère le point R appartenant à la courbe sachant que son ordonnée est 8 et son abscisse négative. Compléter la colonne du tableau correspondant à ce point.
Placer dans le repère, deux points S et T de votre choix appartenant à la courbe. Compléter les colonnes du tableau correspondant à ces points.

Points	P	Q	R	S	T
Abscisse	x = ………	x = ………	x = ………	x = ………	x = ………
Ordonnée	y = ………	y = ………	y = ………	y = ………	y = ………
Relation : f(x) = y	f (….) = …..	f (….) = …..	f (….) = …..	f (….) = …..	f (….) = …..

2. Résoudre les questions suivantes graphiquement (on laissera les traits de construction apparents ) .

Quel est l’image de – 2 par f ?

Quelle est la valeur de f (- 1 ) ?

Quel(s) est l’antécédent de – 3 ?

Résoudre graphiquement f (x) =7 .

Quel(s) nombre a pour image – 4 ?

Quelle est la valeur de f ( – 5) ?

Exercice 3 :

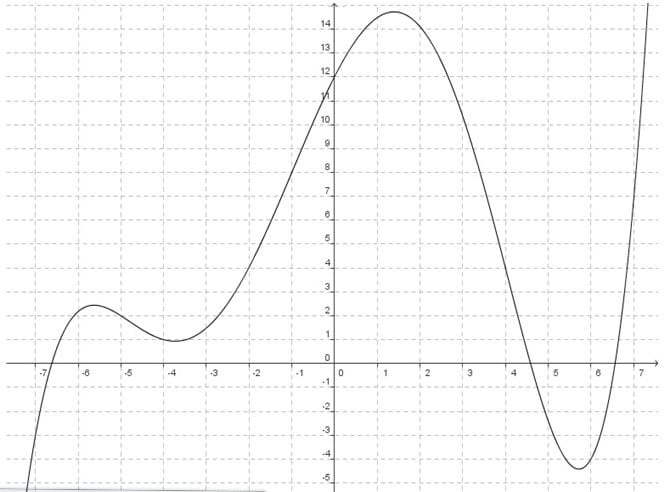
f est la fonction définie par ce graphique.

a. Lire l’image de 0.
b. Lire l’image de 4.
c. Lire les antécédents de 0.
d. Lire approximativement les antécédents de 1.

Exercice 4 :

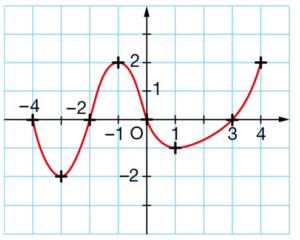
g est la fonction définie par le graphique ci-dessous.

a. Lire l’image de 0.
b. Lire les antécédents de 1 , puis celui de -2.
c. Citer un nombre qui n’a pas d’antécédent.
d. Citer un nombre qui a trois antécédents.

Exercice 5 :

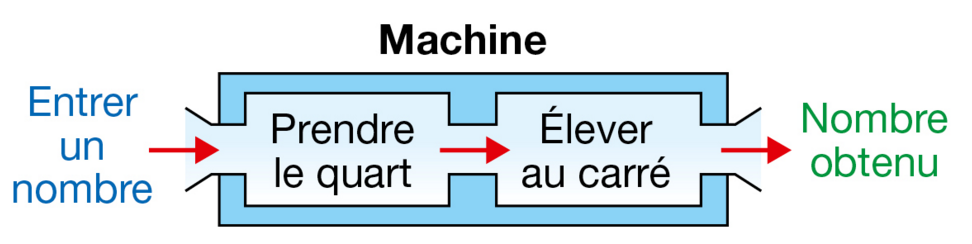
Voici une machine que l’on assimile à une fonction .

a. Vérifier que si l’on entre le nombre 20, alors on obtient le nombre 25.
b. Que signifie l’écriture p (—12) = 9 pour cette machine ?
Vérifier que cette égalité est vraie.

Exercice 6 :

Voici des informations sur une fonction h.

1.Quelle est l’image par la fonction h du nombre :
$a.\,-1?\,\,\,;b.\,1?\,\,\,;c.\,5?;$
2.Citer un antécédent par la fonction h du nombre :

$a.\,-2\,\,\,;b.\,3\,\,\,;c.\,0;$

3. Citer un nombre dont l’image par h est 2.

Exercice 7 :

Théo a complété un tableau de valeurs de la fonction $g\,:\,x\,\mapsto \,2x+\,3$ .
Voici le tableau qu’il a obtenu.

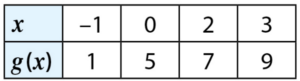
Il a commis une erreur.
Retrouver cette erreur et la corriger.

Exercice 8 :

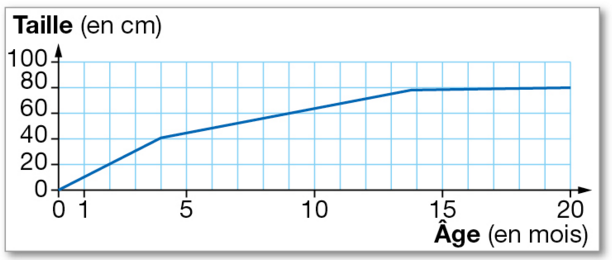
Le graphique qui suit donne l’évolution de la taille (en cm) d’un jeune tigre du Bengale
en fonction de son âge (en mois).

a. Lire de façon exacte la taille du tigre à 2 mois, puis à 9 mois.
b. Lire de façon approchée l’âge du tigre lorsqu’il mesure 45 cm, puis 80 cm.

Exercice 9 :

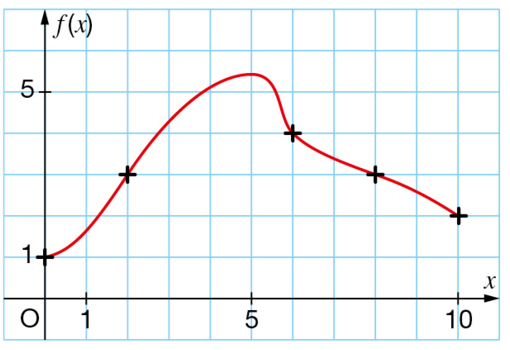
f est la fonction définie par ce graphique.

1 . Lire de façon exacte :
a. l’image de : .10 .6 .2
b. le ou les antécédents de : .3 .1
2. Lire de façon approchée :
a. l’image de : .1 .5
b. les antécédents de : .2 .5
Exercice 10 :

Voici un programme de calcul.

a. Quel résultat obtient-on lorsqu’on choisit le nombre 5 ?
b. On note f la fonction qui, au nombre choisi, associe le résultat obtenu.
Calculer f(-4).

Exercice 11 :

Pour chaque situation, imaginer une fonction associant une grandeur à une autre.

Exercice 12 :

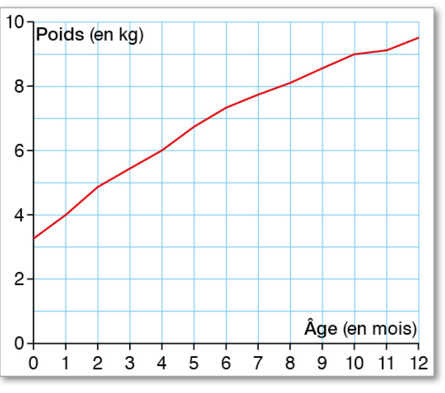
Ce graphique donne l’évolution du poids d’un enfant en fonction de son âge durant sa première
année.

a. Recopier et compléter : « Ce graphique définit une fonction p qui, à … , associe … .»
b. Quel était le poids de l’enfant 4 mois ?
c. A quel âge l’enfant pesait-il 4 kg ? 9 kg ?
d. Interpréter l’égalité p(0) = 3,3 pour la situation.

Exercice 13 :

f est la fonction définie par ce graphique.
Sur quel axe lit-on :
a. les images ?
b. les antécédents ?
2. Lire :

3. Citer un nombre qui :

a. n’a aucun antécédent ;
b. a un seul antécédent ;
c. a deux antécédents ;
d. a trois antécédents.

4. Karim affirme : « Il y a un nombre qui a plus de trois antécédents. »
A-t-il raison ? Expliquer.

Exercice 14 :

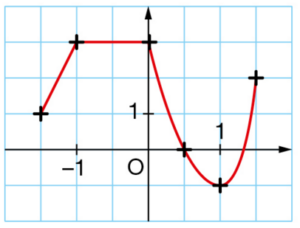
Ce graphique définit une fonction g.

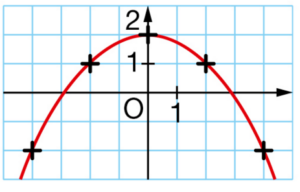
a. Lire l’image de 2, puis de 0 par la fonction g.
b. Lire les antécédents de -2 par la fonction g.

Exercice 15 :

g est la fonction définie par le tableau suivant :

a. Donner l’image de : •2 •- 2 •5

b. Donner un antécédent de : •2 •- 2 •5

c. Léa affirme : «g(10) = – 3»

A-t-elle raison ? Si non, expliquer son erreur.
d. On recherche un nombre tel que h () = 10.
Indiquer une (des) valeur(s) possible(s) de .

Exercice 16 :

h est la fonction définie par $h\,(x)\,=\,-7x$ .

Exercice 17 :

Voici un programme de calcul.

• Calculer son carré.
1.a. Marc choisit 2 pour nombre de départ et obtient 30.

Est-ce exact ?
b. Robin choisit 0, 1 pour nombre de départ.
Quel résultat obtient-il ?
2.a. On note p la fonction qui, au nombre x choisi, associe le résultat obtenu.
Déterminer l’expression de p (x).
b. Calculer .
c. Vérifier que 0,2 est un antécédent de 10,2.

Exercice 18 :

x désigne un nombre positif.
On note la fonction qui, une longueur x en cm, associe l’aire, en cm², du triangle
rectangle représenté ci-dessous.

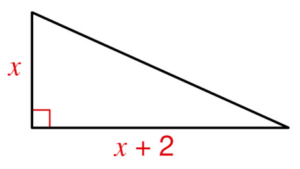
a. Calculer A(3) .
b. Donner l’expression de A(x) .
c. Est-il vrai que 5 est un antécédent de 17,5 par la fonction ?

Exercice 19 :

g est la fonction définie par $g(x)\,=\frac{x}{5}+1$ .

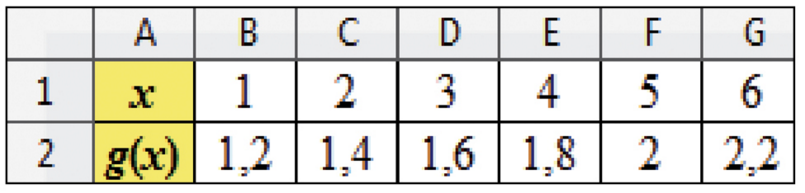
1.Voici un tableau de valeurs obtenu avec le tableur.

2. Quelle formule a-t-on saisie en cellule B2, puis étendue vers la droite ?
Pour chaque affirmation, dire si elle est vraie ou fausse. Justifier.
a. L’image de 5 est 2.

b. $g(\frac{1}{2})=11$

c. $g(3)=\frac{8}{5}$

d. 0 n’a pas d’image.

e. 15 a pour antécédent -2.

Exercice 20 :

Effectuer ce QCM portant sur les généralités sur les fonctions numériques.

Voir Exercices 11 à 20...

Télécharger puis imprimer cette fiche en PDF.

Télécharger ou imprimer cette fiche «fonctions : exercices de maths en 3ème corrigés en PDF.» au format PDF afin de pouvoir travailler en totale autonomie.

Vous devez vous inscrire ou vous connecter à votre compte afin de pouvoir télécharger ce document au format PDF.

Réviser les cours et exercices avec nos Q.C.M :

Q.C.M en 6ème Q.C.M en 5ème Q.C.M en 4ème Q.C.M en 3ème Q.C.M en 2de Q.C.M en 1ère Q.C.M en Terminale

D'autres ressources pour progresser en autonomie :

Chronomètre Horloge France Tables Multiplication Arrondir des décimaux Rapporteur et Angles Médiatrice Symétrie Axiale d'un triangle Symétrie Centrale d'un triangle Translation d'un triangle Rotation Homothétie Bissectrice Tracer droite parallèle Conversion Aires et Volumes Addition de deux relatifs Soustraction Relatifs Addition et soustraction de trois relatifs Produit Deux Relatifs Produit Trois Relatifs Quotient Relatifs Carré Entier Racine Carrée Théorème Pythagore Liste Diviseurs Décomposition Facteurs Premiers Calcul du PGCD PGCD Algorithme Euclide Test Nombre Premier Déterminer Fonction Linéaire Déterminer Fonction Affine Traceur Courbe Trigonométrie Angle Trigonométrie Longueur Périmètre d'un Cercle Aire d'un Disque Volume du Parallélépipède Rectangle Volume du cylindre Surface d'une Sphère et Volume d'une boule Volume d'une pyramide à base rectangulaire Section d'une pyramide Visualiser Section Cône en 2D Section d'un Cône Carte Mondiale Coordonnées Géographiques

Mathématiques Web c'est 2 253 856 fiches de cours et d'exercices téléchargées.