Probabilités : exercices de maths en 3ème corrigés en PDF.

Les probabilités avec une série d’exercices de maths en 3ème corrigés qui vous aidera à bien vous entraîner. Les probabilités sont à traiter avec une grande concentration et une certaine logique. En effet, elles font intervenir votre intelligence et vos compétences. Elles s’utilisent aussi dans la vie de tous les jours. De plus, ces énoncés font intervenir les notions suivantes :

définition d’une expérience aléatoire;
définition d’une issue et d’un événement;
arbre de probabilités;
calcul de probabilités.

Ces énoncés corrigés sont à télécharger gratuitement au format PDF.

Exercice 1 :

La roue de loterie ci-dessous est équilibrée et partagée en huit secteurs identiques.

On fait tourner la roue et on observe le numéro repéré.

Expliquer pourquoi l’événement E : « Le numéro repéré est divisible par 4 » et son événement
contraire ont la même probabilité.

Exercice 2 :

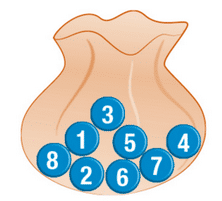
Un sac opaque contient huit jetons numérotés de 1 à 8.

On tire au hasard un jeton et on note son numéro.

1.Dans chaque cas, indiquer les issues qui réalisent
l’événement :

a. : « Obtenir un multiple de 2 »;

b.: « Obtenir un nombre supérieur ou égal à 4 »;
c. : « Obtenir un nombre pair supérieur ou égal à 4 ».

2.Donner l’écriture décimale de chaque probabilité.
a. P() b. P() c.P()

Exercice 3 :

On tire au hasard une carte dans un jeu de 32 cartes.

1.a. Combien l’expérience compte-t-elle d’issues ?
b. Quelle est la probabilité de chaque issue ?

2.a. Indiquer les issues qui réalisent chacun des événements:

E:« La couleur de la carte tirée est rouge (cœur ou carreau) » ;
F:«La carte tirée est un as ».

b. Donner la probabilité de chacun de ces événements.

3.Existe-t-il des issues qui réalisent les deux événements E et F en même temps ?
Quelles sont-elles ?

Exercice 4 :

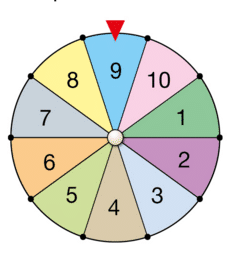
La roue équilibrée ci-dessous est partagée en dix secteurs identiques numérotés de 1 à 10.

Léa fait tourner la roue et observe le numéro repéré.
Elle s’intéresse aux événements suivants :

E:«Le numéro repéré est pair »;
F:«Le numéro repéré est multiple de 3»;
G:« Le numéro repéré est multiple de 5 ».

1. Dresser la liste des issues qui réalisent chacun des événements E, F et G.

2.Dans chaque cas, dire si les événements sont incompatibles ou non. Justifier la réponse.
a. E et F b. E et G c. F et G

3.Donner la probabilité de chacun des événements E, F et G.

Exercice 5 :

Mathis lance une pièce équilibrée de 1€, note le résultat :
Pile (P) ou Face (F), puis tire au hasard une boule du sac et observe sa couleur : rouge (R), vert (V),
bleu (B), noir (N) ou jaune (J).

1. a. Recopier et compléter l’arbre ci-dessous.

b. Combien l’expérience compte-t-elle d’issues ?

2.Donner la probabilité de chacun des événements :

: « Obtenir la couleur rouge »;
:« Ne pas obtenir la couleur jaune ».

Exercice 6 :

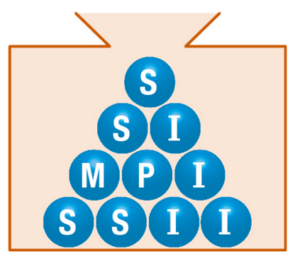
Une urne opaque contient dix boules.

Sur chacune d’elles est inscrite une des lettres du mot : MISSISSIPI.
On tire une boule au hasard de l’urne et on lit la lettre obtenue.

a. Dessiner l’arbre des issues pondéré par les probabilités écrites sous forme de fractions irréductibles.
b. Calculer la probabilité de l’événement E : « La lettre obtenue n’est pas une voyelle ».

Exercice 7 :

Un commerçant propose des boissons sur un marché.
Dans son réfrigérateur, on trouve 30 bouteilles de thé glacé (T),

32 de jus d’ananas (J), 18 de soda (S) et 40 d’eau gazeuse (E).
Ces bouteilles sont de même forme.
Le commerçant prélève au hasard une bouteille dans son réfrigérateur.
a. Dessiner l’arbre des issues pondéré par les probabilités écrites sous forme de fractions irréductibles.
b. Calculer la probabilité de l’événement E: « La bouteille n’est pas une bouteille d’eau gazeuse ».

Exercice 8 :

Tania lance au hasard un dé dont les faces sont numérotées de 1 à 6.

Elle lit le numéro sorti.
E est l’événement : « Tania lit un nombre pair ».
Citer les issues qui réalisent E, puis celles qui réalisent son événement contraire $\,\overline{E}$ .

Exercice 9 :

On lance deux fois de suite une pièce de monnaie.
On note E l’événement : « Obtenir au moins une fois Pile ».
Énoncer l'(les) issue(s) qui réalise(nt) l’événement contraire de E.

Exercice 10 :

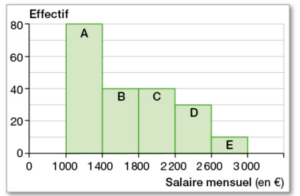
Voici la répartition des salaires dans une entreprise.
On compte cinq catégories de salaires : A, B, C, D et E.

Par exemple, un salarié de la catégorie A touche un salaire mensuel compris

entre 1 000 € inclus et 1 400 € exclu.
On rencontre au hasard un salarié de l’entreprise et
on lui demande sa catégorie de salaire.
a. Dessiner l’arbre des issues pondéré par les probabilités écrites sous forme

de fractions irréductibles.
b. Donner la probabilité de chacun des événements :
• U : « Le salarié gagne au moins 1 800 € par mois » ;
• V : « Le salarié gagne strictement moins de 2 200 €
par mois ».

Exercice 11 :

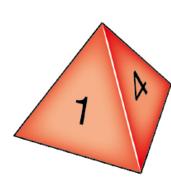
On lance deux fois de suite un dé équilibré a quatre faces numérotées de 1
à 4.
:
On repère à chaque lancer le numéro qui figure sur la face cachée du dé.

1 .a. Dessiner un arbre afin d’obtenir toutes les issues de l’expérience.
b. Quelle est la probabilité de chaque issue ?
2.a. Donner les issues qui réalisent l’événement :
E : « La somme des deux numéros est égale à 5 ».
b. Quelle est la probabilité de cet événement ?
3. Que dire de chaque événement ?
a. F : « La somme des deux numéros est égale à 1 ».
b. G : « La somme des deux numéros est inférieure à 10».

Exercice 12 :

Dans son dressing, Sarah possède quatre robes (une blanche, une noire, une rouge et une bleue) et
deux chapeaux (un rouge et un bleu).
Ce matin, elle choisit au hasard une robe et un chapeau.

a. Dessiner un arbre afin d’obtenir toutes les issues de l’expérience.
b. E est l’événement : « Sarah a choisi une robe et un chapeau de la même couleur ».
Quelle est la probabilité de cet événement ?
c. Définir l’événement contraire de E et calculer sa probabilité.

Exercice 13 :

Sur chacun des morceaux de papier représentés
ci-dessous, Antoine a écrit une lettre du mot ROSE.

Il place ces morceaux de papier dans un sac, puis il
tire au hasard un 1er morceau de papier, le remet dans
le sac et tire un 2e morceau de papier. Il lit les lettres obtenues.
1 .a. Dessiner un arbre afin d’énumérer les issues de l’expérience.
b. Quelle est la probabilité de chaque issue ?
2. Antoine s’intéresse à l’événement :
M : « J’ai tiré au moins une fois la lettre O ».
a. Définir l’événement contraire $\,\overline{M}$ de M.
b. Donner la probabilité de l’événement $\,\overline{M}$ .
c. En déduire la probabilité de l’événement M.
d. Retrouver la probabilité P(M) d’une autre façon.

Exercice 14 :

On écrit sur les faces d’un dé équilibré chacune des lettres du mot ARMURE.
On lance ce dé et on lit la lettre inscrite sur la face supérieure.

l. a. Quelles sont les issues de cette expérience ?
b. Donner la probabilité de chacune d’elles.
2. Déterminer la probabilité de l’événement :
a. : « Obtenir une lettre du mot RAMEUR » ;
b. : « Obtenir une lettre du mot COTON » ;
c. : « Obtenir une lettre du mot MALIN » ;
d. : « Obtenir une consonne ».

Exercice 15 :

4.1/5 - (11 votes)

Télécharger puis imprimer cette fiche en PDF.

Télécharger ou imprimer cette fiche «probabilités : exercices de maths en 3ème corrigés en PDF.» au format PDF afin de pouvoir travailler en totale autonomie.

D'autres cours et exercices à consulter

Mathématiques Web c'est 2 268 052 fiches de cours et d'exercices téléchargées.