Théorème de Thalès : exercices de maths en 3ème corrigés.

Le théorème de Thalès à travers des exercices de maths en 3ème corrigés vous aidera à compenser vos lacunes. Ainsi, il faut savoir que le chapitre est parmi les plus importants car l’élève en fera usage tout au long de l’année.

Vous retrouverez dans cette série d’énoncés les notions suivantes :

partie directe et réciproques;
produit en croix;
proportionnalité des longueurs;
coefficient de réduction ou d’agrandissement;
droites parallèles.

En classe de troisième, les élèves étudient ce théorème et son application dans divers contextes. Ces énoncés corrigés ont été rédigés par un enseignant et sont à consulter en ligne ou à télécharger au format PDF.

Exercice 1 :

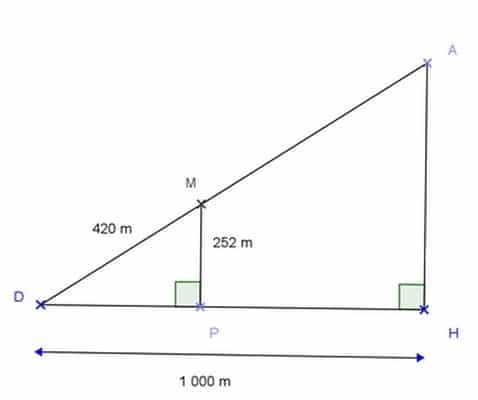
Un funiculaire part de D pour se rendre à A suivant la droite (DA) .

DM = 420 m ; DH = 1 000 m;

MP = 252 m.

Les triangles DPM et DAH sont respectivement rectangles en P et H.

1) Calculer la distance DP en mètre.

2) a) Démontrer que les droites (MP) et (HA) sont parallèles.

b) Calculer la distance DA en mètre puis en kilomètre.

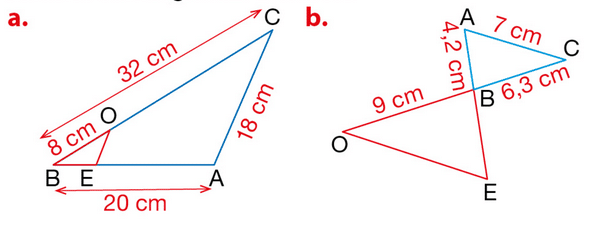
Exercice 2 :

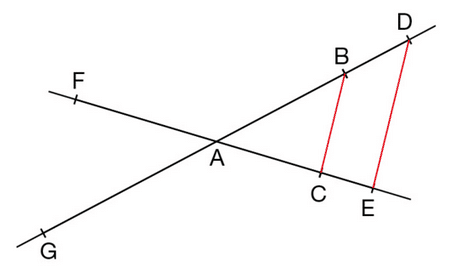
Les droites (BD) et (CE) se coupent en A et les droites (BC) et (DE) sont parallèles.

AC=3cm; AE=4,5 cm; AB = 4 cm et DE = 4,2 cm.

a. Calculer les longueurs AD et BC.
b. F et G sont les points indiqués des droites (AC) et (AB) tels que :
AF = 4,05 cm et AG= 5,4 cm.
Montrer que les droites (FG) et (BC) sont parallèles.

Exercice 3 :

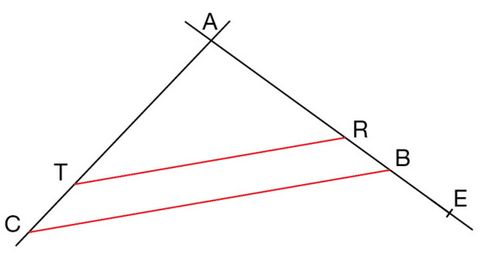
Les droites (BC) et (RT) sont parallèles.
Les points R et E appartiennent à la droite (AB) et le point T appartient à la droite (AC).
On donne :
AB=6 cm ; AC=72 cm ; BC=10 cm;
AR=4,5 cm et BE =2 cm.

a. Calculer AT,TR et AE.
b. Les droites (BT) et (EC) sont-elles parallèles ?

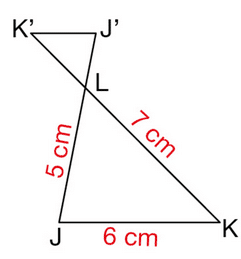
Exercice 4 : théorème de Thalès

Le triangle LJ’K’ est l’image du triangle LJK par l’homothétie de centre Let de rapport – 0,4.

Donner les longueurs des trois côtés du triangle LJ’K’.

Exercice 5 :

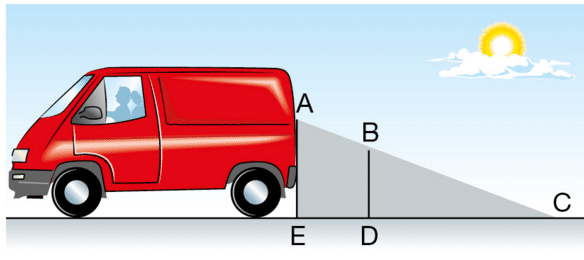
Sur le schéma, la zone grisée correspond à ce que le conducteur d’un véhicule ne voit pas lors d’une
marche arrière.

Données :

(AE) // (BD)
AE = 1,50 m
ED = 1,10 m
EC =6 m

a. Calculer DC.
b. En déduire que ED = 1,60 m.
c. Une fillette mesure 1,10 m.
Elle passe à 1,40 m derrière la camionnette.
Le conducteur peut-il la voir ? Expliquer.

Exercice 6 :

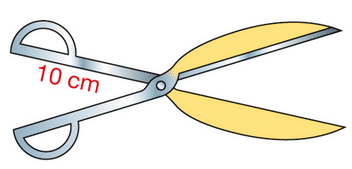
On souhaite fabriquer des cisailles de façon qu’à un écartement de 14 cm des poignées de la cisaille
corresponde une ouverture de 50 cm des lames, en jaune sur le schéma (le dessin n’est pas à l’échelle).
a. Représenter cette situation par un croquis à main levée et coder les longueurs connues.

b. Calculer une valeur approchée de la longueur des lames du ciseau.

Exercice 7 :

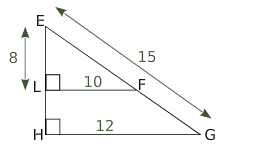
1.Démontrer que les droites (LF) et (HG) sont parallèles.

2.Calculer EF, EH et FG.

Exercice 8 :

Sur la figure ci-dessous, BR=2,5 cm, BL=15 cm, BE=1,5 cm et BI = 9 cm.

Les points I,B et E sont alignés dans le même ordre que L,B,R.

Montrer que les droites (IL) et (ER) sont parallèles.

Exercice 9 :

Dans chaque cas, on passe du triangle OBE au triangle ABC par une homothétie.
Donner le centre et le rapport de l’homothétie, puis calculer les longueurs OE et BE.

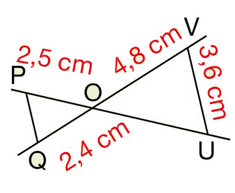
Exercice 10 :

Les points O, P et U sont alignés ainsi que les points O, Q et V.
Les droites (QP) et (VU) sont parallèles.
Calculer mentalement OU et QP.

Exercice 11 :

Les droites (BN) et (CM) se coupent en A.
Dans chaque cas, déterminer si les droites (BC) et (MN) sont parallèles ou non.

Exercice 12 :

La tour du One World Trade Center a été inaugurée en 2014, à New York (États-Unis).

Une personne de 1,65 m, située à 100 m de la tour, mesure $\widehat{HOP} = 79,5 ^{\circ}$ (O représente son œil).

Calculer une valeur approchée à l’unité près de la hauteur, en m, de cette tour.

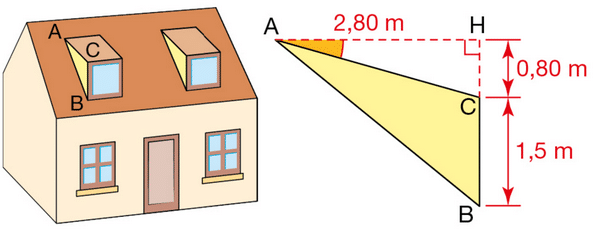
Exercice 13 :

Voici un plan de coupe de l’une des deux lucarnes de cette maison.

Déterminer une valeur approchée au degré près de :
a. la mesure de $\widehat{HAC}$ ,
b. la mesure de $\widehat{HAB}$ ,
c. la mesure de $\widehat{CAB}$ .

Exercice 14 :

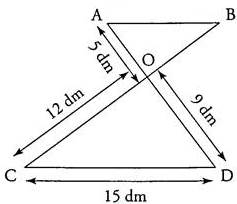
Les droites (NM) et (AC) sont parallèles et les longueurs sont exprimées en cm.

Calculer la valeur de NM (donner la valeur exacte et la valeur approchée au millimètre).

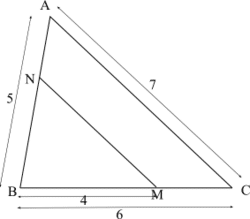
Exercice 15 :

Les droites (AD) et (CE) sont parallèles.

Calculer la valeur de CE (donner la valeur exacte et la valeur approchée au millimètre)

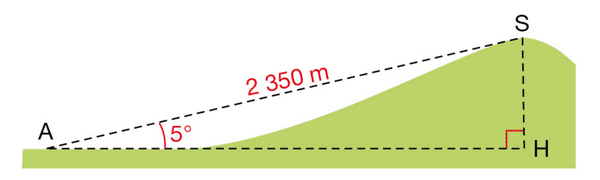
Exercice 16 :

LU Un géomètre, positionné en À, souhaite calculer l’altitude du sommet S d’une colline.

Son GPS lui indique qu’il se trouve lui-même à une altitude de 625 m.

Il’effectue les mesures suivantes :

a. Donner une valeur approchée au centième près de
la hauteur HS, en m, de la colline.
b. En déduire l’altitude du point S.

Exercice 17 :

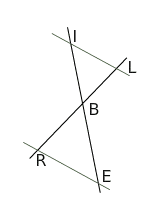
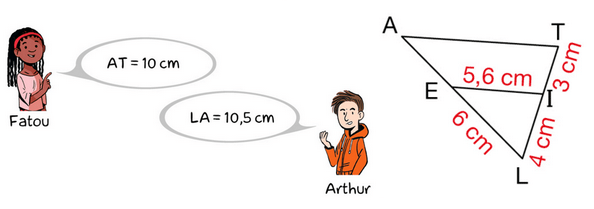
Sur la figure ci-dessous :

– les droites (AE) et (TI) sont sécantes en L;

– les droites (EI) et (AT) sont parallèles.

Que peut-on penser des affirmations de Fatou et d’Arthur ?

Exercice 18 :

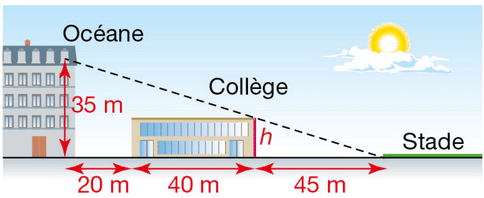
Océane peut, malgré le collège, voir de sa fenêtre le stade dans son intégralité.

Calculer la hauteur h du collège.
On considérera que les murs verticaux sont parallèles.

Exercice 19 :

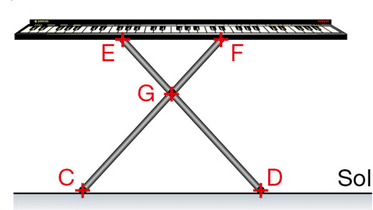
Pour ce piano :
GE= 48 cm;
GF=60cm;
ED=1,2met
C=1,5m.
Le sol est représenté par la droite (CD).
Le clavier est-il parallèle au sol ?

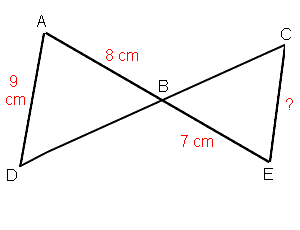
Exercice 20 :

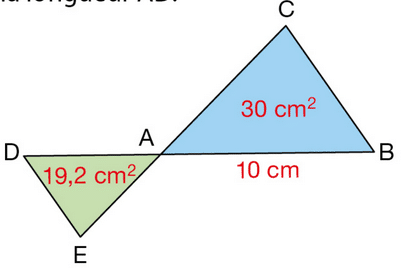
Les droites (DB) et (CE) se coupent en A et les droites (DE) et (CB) sont parallèles.
Calculer la longueur AD.

Exercice 21 :

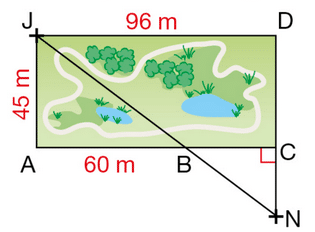
Noé (N) doit rejoindre sa sœur Juliette (J).

Il coupe à travers le parc en passant par le point B.
Le parc est représenté par le rectangle AJDC.

Quelle distance Noé va-t-il parcourir ?

Exercice 22 :

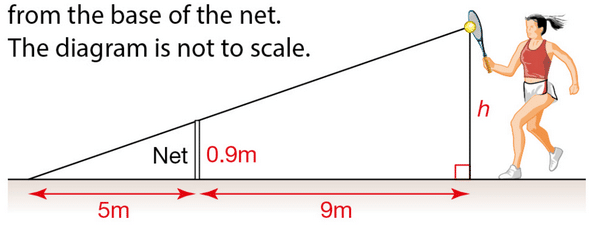
Find the value of the height h, in the following diagram, at which the tennis ball must be hit so that
it will just pass over the net and land 5 meters away from the base of the net.

The diagram is not to scale.

Exercice 23 :

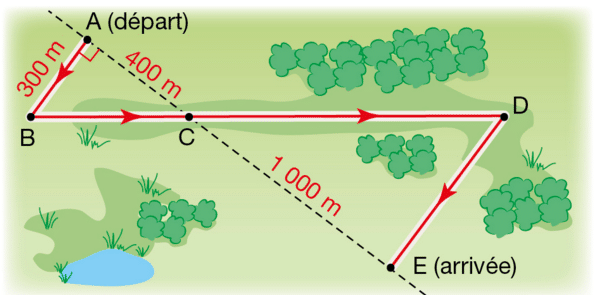
Des élèves participent à une course.
Avant l’épreuve, un plan leur a été remis.
Il est représenté par la figure ci-dessous.

On convient que :

les droites (AE) et (BD) se coupent en C,
les droites (AB) et (DE) sont parallèles,
ABC est un triangle rectangle en A.

Calculer la longueur réelle du parcours ABCDE.

Exercice 24 :

Les questions 2, 3 et 4 sont indépendantes. L’unité est le centimètre.
1) Construire un triangle MAI rectangle en A tel que AM = 8 et IM = 12. Indiquer brièvement les étapes de la construction.
2) Calculer la valeur exacte de AI.
3) R est le point du segment [MI] tel que MR = 9.
La parallèle à (AI) passant par R coupe [AM] en E.
Calculer ME.
4) Calculer $cos ( \widehat{AMI} )$ .
En déduire la valeur arrondie au degré de $\widehat{AMI}$ .

Exercice 25 :

Soit un triangle ADE rectangle en A tel que :
AD = 5 cm et AE = 3 cm.
B est le point de la demi-droite [AD) tel que BA = 8 cm.
La parallèle à la droite (DE) passant par B coupe (AE) en C.
1) Faire la figure.
2) Calculer DE. En donner une valeur arrondie au mm près.
3) Calculer AC.
4) Calculer BC. En donner une valeur arrondie au mm près.
5) Calculer $tan(\widehat{AED})$ .
6) En déduire la mesure de l’angle $\widehat{AED}$ arrondie au degré.

Exercice 26 :

Soit IJK un triangle rectangle en I tel que IJ = 3,6 cm et IK = 4,8 cm.

On place le point L de la demi-droite [KI) tel que KL = 8 cm.

La parallèle à la droite (IJ) passant par L coupe (KJ) en M.

La figure ci-contre n’est pas en vraie grandeur, elle n’est pas à reproduire.

1) Démontrer que KJ = 6 cm.

2) Calculer la valeur de KM, en justifiant la réponse.

3) Déterminer une mesure de l’angle $\widehat{IKJ}$ à 1 degré près.

Exercice 27 :

On considère le triangle ABC rectangle en A tel que AB = 5, BC = 9, l’unité étant le cm.

1) Construire le triangle ABC en vraie grandeur.

2) Calculer la valeur exacte de AC.

3) Calculer la mesure de l’angle à un degré près par défaut.

4) Le cercle de centre B et de rayon AB coupe le segment [BC] en M. La parallèle à la droite (AC) qui passe par M coupe le segment [AB] en N.

Compléter la figure.
Calculer la valeur exacte de BN.

Exercice 28 :

Un fabricant d’enseignes lumineuses doit réaliser la lettre z (en tubes de verre soudés) pour la fixer sur le haut d’une vitrine. Voici le schéma donnant la forme et certaines dimensions de l’enseigne :

Les droites (AD) et (BC) se coupent en O.

Sachant que les droites (AB) et (CD) sont parallèles, calculer les longueurs AB et OB (donner les résultats sous forme fractionnaire).
Démontrer que le tube [BC] est perpendiculaire à la droite (AD).
Calculer $sin(\widehat{OCD})$ .

En déduire la valeur arrondie de l’angle $\widehat{OCD}$ à un degré prés.

Exercice 29 :

Soit ABC un triangle tel que : AB = 4,5 cm BC = 7,5 cm AC = 6 cm

Construire un tel triangle.
Démontrer que le triangle ABC est rectangle.
Calculer à un degré près l’angle .
M est le point du segment [AB] tel que AM = 1,5 cm, et N est le point du segment [AC] tel que NC = 4 cm.

Les droites (MN) et (BC) sont-elles parallèles? Justifier.

Exercice 30 :

L’unité est le centimètre.

Construire un triangle RST tel que : RS = 4,5 ST = 6 RT = 7,5

On laissera les traits de construction.

Montrer que le triangle RST est rectangle.
a) Tracer le cercle (C) de centre R et de rayon 4,5. Le cercle (C) coupe le segment [RT] en K.
b) Tracer la droite d passant par le point K et parallèle à la droite (RS).

cette droite d coupe le segment [TS] en un point L.

Placer ce point sur la figure.

c) Calculer KL.
Calculer l’angle $\widehat{STR}$ (on donnera l’arrondi au degré).

Exercice 31 :

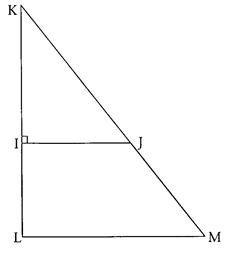
Construire le cercle (C) de centre O et de rayon 4 cm. Tracer un diamètre [AB] de ce cercle.

Construire le point S symétrique du point O par rapport au point A, puis le cercle (C’) de diamètre [OS]. Le cercle (C’) coupe le cercle (C) en deux points T et T’.

a) Démontrer que le triangle SOT est rectangle en T
b) Que représente la droite (ST) pour le cercle (C) ? Justifier.
Déterminer la mesure de l’angle .
La droite passant par B et parallèle à la droite (OT) coupe la droite (ST) en P
a) Construire la droite (BP).
b) Calculer BP

Télécharger puis imprimer cette fiche en PDF.

Télécharger ou imprimer cette fiche «théorème de Thalès : exercices de maths en 3ème corrigés en PDF.» au format PDF afin de pouvoir travailler en totale autonomie.

Vous devez vous inscrire ou vous connecter à votre compte afin de pouvoir télécharger ce document au format PDF.

D'autres cours et exercices à consulter

Mathématiques Web c'est 2 268 671 fiches de cours et d'exercices téléchargées.