Fonctions linéaires : cours de maths en 3ème avec leçon en PDF.

sommaire

1 I. Les fonctions linéaires :
2 II. Fonctions linéaires et pourcentages
- 2.1 1.Pourcentages d’augmentation et de diminution
- 2.2 2.Application des pourcentages aux fonctions linéaires

Un cours sur les fonctions linéaires avec la définition, le vocabulaire et ses propriétés ainsi que l’étude des pourcentages. L’élève devra bien maîtriser la notion de proportionnalité qui amène à une fonction linéaire. développer des compétences en sachant calculer une image ou un antécédent, ou encore, tracer la courbe d’une fonction linéaire ou savoir déterminer la valeur du coefficient directeur en troisième.

I. Les fonctions linéaires :

1.Définition et vocabulaire

Définition :

Soit « a » un nombre fixé. En associant à chaque nombre « x » un nombre « ax » appelé « image de x », on définit une fonction linéaire de coefficient a.

On notera cette fonction ainsi : $f:x \mapsto ax$

L’image de x sera notée : f(x).

x est appelé l’antécédent de f(x)

Exemple :

Soit f est la fonction linéaire de coefficient 2.

On la note : $f:x \mapsto 2x$

alors :

L’image de 5 est : $f(5) = 2\times 5 = 10$ .
L’image de (-3) est : $f(-3) = 2 \times (-3) = -6$ .
L’image de 1 est : $f(1) = 2 \times 1 = 2$ .

Remarque :

On peut regrouper ces résultats dans un tableau :

x	5	-3	1
f(x)	10	-6	2

C’est un tableau de proportionnalité. Et le coefficient de proportionnalité qui permet d’exprimer f(x) en fonction de x est 2 ! D’où l’égalité : .

2.Représentation graphique :

Propriété et vocabulaire :

Soit f la fonction linéaire définie par : $f : x \mapsto ax$ L’ensemble des points de coordonnées est appelé représentation graphique de la fonction linéaire.

Dans un repère, cette représentation est la droite passant par :

L’origine du repère.
Le point de coordonnées .

On dit que cette droite a pour équation : .

« a » est le coefficient directeur de la droite. Il indique « l’inclinaison » de la droite.

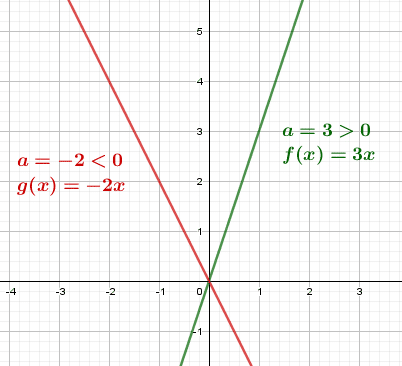
3.Sens de variation d’une fonction linéaire :

Propriété :

Si a>0 alors la fonction linéaire est croissante;
Si a<0 alors la fonction linéaire est décroissante.

Remarque :

Si a = 0, la représentation la droite se confond avec l’axe des abscisses.

II. Fonctions linéaires et pourcentages

1.Pourcentages d’augmentation et de diminution

Propriété :

Augmenter un nombre de t % revient à multiplier ce nombre par $k=1+\frac{t}{100}$ .
Diminuer un nombre de t% revient à multiplier ce nombre par $k=1-\frac{t}{100}$ .

Exemples :
Si une boite de 400 g est vendue avec 25% de produit en plus, sa nouvelle masse (en g) est :

$m = 400 \times ( 1+\frac{4}{100} ) = 400\times 1,25 =500$ , c’est à dire m = 500 g.

En France, une baisse de 4% a été enregistrée sur un effectif annuel de 750 000 naissances.
Le nouvel effectif est :

$N = 750 000 \times ( 1-\frac{4}{100} ) = 750 000\times 0,96=720\,000$ c’est à dire N = 720 000.

2.Application des pourcentages aux fonctions linéaires

	Prendre 5% de x.	Augmenter x de 5%.	Diminuer x de 5%.
Calcul à effectuer	Multiplier par 0,05	Multiplier par 1,05	Multiplier par 0,95
Fonction linéaire	$f : x \mapsto 0,05 x$	$g : x \mapsto 1,05 x$	$h : x \mapsto 0,95 x$
Exemple :	Prendre 5% de 20 : $f(20) = 0,05 \times 20 = 1$	Augmenter 20 de 5% : $g(20) = 1,05 \times 20 = 21$	Diminuer 20 de 5% : $h(20) = 0,95 \times 20 = 19$

Propriété :

De manière générale, on peut associer une fonction linéaire à toute variation de k %.Notons la fonction f qui à la valeur x de départ associe la valeur f(x) après variation.

Pour une augmentation de k %, nous avons $f(x)= ( 1+\frac{k}{100} )x$ .
Pour une réduction de k %, nous avons $f(x)= ( 1-\frac{k}{100} )x$ .

5/5 - (4 votes)

Télécharger puis imprimer cette fiche en PDF

Télécharger ou imprimer cette fiche «fonctions linéaires : cours de maths en 3ème avec leçon en PDF.» au format PDF afin de pouvoir travailler en totale autonomie.

Télécharger nos applications gratuites Mathématiques Web avec tous les cours,exercices corrigés.

D'autres articles analogues à fonctions linéaires : cours de maths en 3ème avec leçon en PDF.

Mathématique web est un site de mathématiques destinés aux élèves et professeurs du collège (6ème, 5ème, 4ème et 3ème) au lycée (2de, 1ère et terminale. Vous trouverez sur ce site de nombreuses ressources vous permettant de vous familiariser avec les mathématiques. Toutes les cours et exercices de maths similaires à fonctions linéaires : cours de maths en 3ème avec leçon en PDF. sont rédigés par des professeurs et sont conformes aux programmes officiels de l'éducation nationale.

Fonctions affines : cours de maths en 3ème avec leçon en PDF.
92
Cours sur les fonctions affines avec la définition, le vocabulaire et les différentes propriétés de ces fonctions. Etude de la courbe représentative et du sens de variation. L'élève devra être capable de calculer une image ou un antécédent mais, également, savoir tracer la courbe d'une fonction affine à l'aide de…
Fonctions : cours de maths en 3ème avec leçon en PDF en troisième.
90
Un cours sur les généralités des fonctions avec la définition d'un antécédent, d'une image et de l'étude de la courbe représentative d'une fonction en 3ème. L'élève devra savoir calculer l'image d'un nombre par une fonction mais aussi déterminer un antécédent par le calcul ou en exploitant la courbe représentative de…
Théorème de Thalès : cours de maths en troisième (3ème)
86
Un cours de mathématiques en troisième sur le théorème de Thalès. Ce cours de maths fait intervenir les notions suivantes : - configurations de Thalès; - partie directe et réciproque; - Produit en croix. Ce cours de mathématiques sur le théorème de Thalès a été rédigé par un enseignant de l'éducation…
Probabilités : cours de maths en 3ème avec leçon en PDF en troisième.
86
Cours de maths en classe de troisième (3ème) sur les probabilités et les expériences aléatoires, définition de l'événement, des issues et du calcul de probabilités à une et deux épreuves. I. Notion de probabilités 1. Les issues et arbre de probabilité Définitions : Une expérience est dite aléatoire lorsque l'on…
Les équations : cours de maths en 3ème avec leçon en PDF en troisième.
83
Un cours sur la résolution d'équations du premier degré à une inconnue et l'étude de problèmes menant à une équation. Nous verrons les différentes propriétés de résolution d'une équation. L'élève devra connaître la définition d'une équation et savoir utiliser les différentes propriétés pour la résoudre. Résoudre des équations-produits et des…

Les dernières fiches mises à jour

Mathématiques Web c'est 2 072 518 fiches de cours et d'exercices téléchargées.
Rejoignez les 46 270 membres de Mathématiques Web, inscription gratuite.