Valeur absolue : exercices de maths en 2de corrigés en PDF.

La valeur absolue d’un nombre avec des exercices de maths en 2de corrigés. L’élève devra connaître sa définition et ses propriétés afin de mener des calculs, mais également, étudier le courbe de la fonction valeur absolue. Ces différents énoncés disposent de leur corrigé afin que l’élève puise relever ses erreurs et progresser en seconde.

Exercice 1 :

Résoudre dans les équations et inéquations suivantes :

a) | 2 – x | < 4

b) | 6 – 2 x | = 3

c) | x + 2 | > 3

d) | x + 2 | < | x + 3 |

e) | x³ – 1 | + p > 0

f) 3 < | x + 2 | < 4

g) | 4 x² – 12 x + 9 | = 4

h) | 3 x + 1 | + | 1 – x | > 3

i) | 1 + x² | = 2x

Exercice 2 :

Calculer.

a) b) c) $|-\frac{100}{3}|$

d) e) $|\sqrt{17}-2|$ f) $|2-\sqrt{17}|$

Exercice 3 :

Sans calculatrice, simplifier :

a) b)

c) $\frac{|5-8|-3}{2}$ d)

Exercice 4 :

1.a) Sur une droite graduée, placer les nombres 5 et $\frac{1}{3}$ .

b) Calculer la distance entre 5 et $\frac{1}{3}$ .

2. Reprendre la question 1. avec 3 et $-\frac{4}{5}$ .

3. Reprendre la question 1. avec -1 et $-\frac{4}{5}$ .

Exercice 5 :

A l’aide d’une valeur absolue, écrire la distance entre :

a) $\frac{125}{3}$ et 2. b) $\sqrt{2}$ et 5

c) – 5 et $\frac{12}{5}$ d) $\pi$ et 4

Exercice 6 :

sans calculatrice, simplifier :

a) $|5-\pi|$ b) $|8-\frac{2}{3}|$ c) $|2-\frac{9}{2}|$

d) e) $|-5-\pi|$ f) $|\frac{1}{2}+6|$

Exercice 7 :

De la même façon que représente la distance entre le nombre réel et 3,

exprimer en termes de distance :

a) b) $|x-\frac{1}{3}|$

c) d)

e) f) $|\pi-x|$

Exercice 8 :

Déterminer l’ensemble, sous la forme d’intervalle, des réels vérifiant :

a) $|x-10|\leq\, 1$ b) $|x-2,5|\leq\, 0,2$ c) $|x-\frac{1}{2}|\leq\, \frac{5}{2}$

Exercice 9 :

On considère un intervalle [a ; b] avec a et b deux nombres réels.

On appelle centre de l’intervalle [a ; b] le nombre $c=\frac{a+b}{2}$
et rayon de l’intervalle [a ; b] le nombre $r=\frac{b-a}{2}$ .
Graphiquement, on a :

1. a) Calculer le centre et le rayon de [2 ; 6].

b) Traduire |x – 4| en termes de distance entre deux réels.
c) Recopier et compléter: $x\in[2;6]\Leftrightarrow |x-4|\leq\, ...$

2. De la même manière, recopier et compléter :
a) $x\in[1;25]\Leftrightarrow |x-13|\leq\, ...$ .
b) $x\in[6;20]\Leftrightarrow |x-...|\leq\, ...$
c) $x\in[1,2;3]\Leftrightarrow |x-...|\leq\, ...$

Exercice 10 :

Ecrire une inégalité vérifiée par et utilisant une valeur absolue dans les cas suivants.

a) $x\in [-4;5]$ b) $x\in [0;1,1]$ a) $x\in [ \frac{1}{3};\frac{2}{3}]$

Exercice 11 :

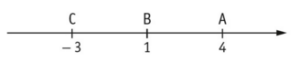
On donne un axe gradué, sur lequel on a placé les points A, B et C.

Compléter les pointillés.

a. AB = …. b. AC = … c. BC = … d. CC = …

Exercice 12 :

On donne un axe gradué, sur lequel on a placé les points A, B et C.

Compléter les pointillés.

a. AB = …. b. AC = … c. BC = …

Exercice 13 :
Ecrire sans les barres de valeurs absolues les nombres :

$a. | (1-\sqrt{2}) ^2 |$

$b. | 2\sqrt{2}-\sqrt{3}|$

$c. | 6-2\pi |$

$d. \frac{ | -2|}{| -5+1|}$

Exercice 14 :

Résoudre dans $\mathbb{R}$ les équations suivantes :

$a. |x |=5\\b. |-x |=19\\c. |x-7 |=0\\d. |x+5,4 |=0\\e. |x-5 |=8\\f. |x-\frac{7}{2} |=2$

Exercice 15 :

Résoudre dans $\mathbb{R}$ les inéquations suivantes :

$a. |x-2 |\leq\, 5\\ b. |x-5 |\leq\, 1\\ c. |x+1,5 |+2,5< 6\\ d. |x-\sqrt{3} | < \sqrt{3}\\ e. |x-2 | \geq\, \sqrt{3}\\ f. |x+\pi | <\sqrt{5}$

Télécharger puis imprimer cette fiche en PDF.

Télécharger ou imprimer cette fiche «valeur absolue : exercices de maths en 2de corrigés en PDF.» au format PDF afin de pouvoir travailler en totale autonomie.

Vous devez vous inscrire ou vous connecter à votre compte afin de pouvoir télécharger ce document au format PDF.

D'autres cours et exercices à consulter

Mathématiques Web c'est 2 268 671 fiches de cours et d'exercices téléchargées.