Géométrie dans l'espace : exercices de maths en 2de corrigés.

La géométrie dans l’espace avec des exercices de maths en 2de corrigés qui vous vous assurent des connaissances approfondies et bien détaillées. L’élève devra être capable de tracer des droites et des plans dans l’espace ainsi que des solides cube, pavé droit, cylindre, pyramide, cône de révolution). Vous devrez savoir déterminer une section de solide et déterminer des équations de droites en étudiant des vecteurs. Ces énoncés disposent de leur corrigé afin que vous puissiez repérer vos lacunes et augmenter vos notes en seconde.

Exercice 1 :

Soit ABCD un tétraèdre et I, J deux points appartenant respectivement aux arêtes [AB] et [BC] tels que (IJ) n’est pas parallèle à (AC). Soit P le plan passant par B et parallèle au plan (IJD). Le but de l’exercice est de tracer l’intersection du plan P avec le plan (ACD).

1) La droite (IJ) coupe la droite (AC) en K. Tracer la droite d’intersection des plans (ACD) et (IJD). Justifier.

2) Soit D la droite d’intersection du plan P et du plan (ABC). Pourquoi a-t-on D parallèle à (IJ) ? Tracer D.

3) La droite D coupe la droite (AC) en L. Soit D’ la droite d’intersection du plan P et du plan (ACD).
Pourquoi a-t-on D’ parallèle à (DK) ? Tracer D’.

Exercice 2 :

Soit une pyramide de sommet S dont la base est un quadrilatère ABCD.
On place I sur [SA] tel que $\vec{SI}=\frac{1}{3}\vec{SA}$ , et J sur [SD] tel que $\vec{SJ}=\frac{1}{3}\vec{SD}$

1) Tracer $\Delta$ l’intersection du plan (CIJ) et du plan de base. Justifier cette construction.

2) Déterminer sans justifier la section de la pyramide par le plan (CIJ)

Exercice 3 :

Soit une pyramide SABCD telle que (AB) et (CD) se coupent en E.

1) Déterminer l’intersection des plans (SAB) et (SDC)

2) Un plan P parallèle à (ES) coupe (SA) en I, (SB) en J, (SC) en K, (SD) en L.
Montrer que (IJ) et (KL) sont parallèles.

Exercice 4 :

Une pyramide SABCD est telle que la base ABCD est un parallélogramme.

Appelons I, J, K les milieux des arêtes [SB], [SC] et [AB]

1) Démontrer que les droites (IJ) et (AD) sont parallèles

2) Déduisez de la question 1) que le plan (SDK) et la droite (IJ) sont sécants

3) Justifiez et construisez l’intersection des plans (SKD) et (SBC)

4) Justifiez et construisez l’intersection de la droite (IJ) avec le plan (SKD)

Exercice 5 :

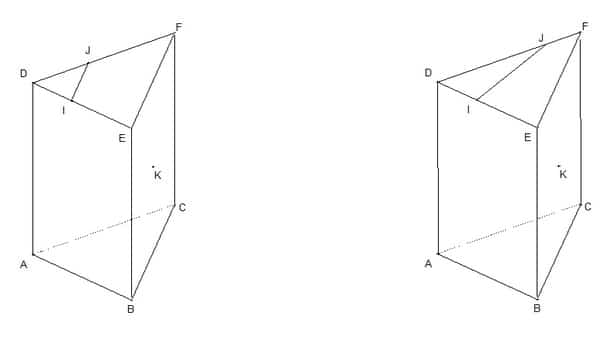
Soit ABCDEF, un prisme droit, I un point de ]DE[, J un point de ]DF[ et K, le centre de la face BCFE du prisme. On s’intéresse à l’intersection des plans (IJK) et (ABC).

1^er cas : (IJ)//(EF)

1) Montrer que l’intersection de (IJK) avec (BCF) est parallèle à (IJ). On appellera $\Delta$ cette intersection.

2) On appelle L l’intersection de $\Delta$ avec (EB) et M l’intersection de D avec (FC). Construire ci-dessous l’intersection de (IJK) avec (ABC). On ne justifiera que l’existence des points supplémentaires nécessaire à la construction ou l’utilisation des propriétés sur le parallélisme.

2^ème cas : (IJ) n’est pas parallèle à (EF). On appellera N leur point d’intersection.

3) Sans justifier, construire ci-dessous l’intersection de (IJK) avec (BCF) puis de (IJK) avec (ABC).

Télécharger puis imprimer cette fiche en PDF.

Télécharger ou imprimer cette fiche «géométrie dans l'espace : exercices de maths en 2de corrigés en PDF.» au format PDF afin de pouvoir travailler en totale autonomie.

Vous devez vous inscrire ou vous connecter à votre compte afin de pouvoir télécharger ce document au format PDF.

Réviser les cours et exercices avec nos Q.C.M :

Q.C.M en 6ème Q.C.M en 5ème Q.C.M en 4ème Q.C.M en 3ème Q.C.M en 2de Q.C.M en 1ère Q.C.M en Terminale

D'autres ressources pour progresser en autonomie :

Chronomètre Horloge France Tables Multiplication Arrondir des décimaux Rapporteur et Angles Médiatrice Symétrie Axiale d'un triangle Symétrie Centrale d'un triangle Translation d'un triangle Rotation Homothétie Bissectrice Tracer droite parallèle Conversion Aires et Volumes Addition de deux relatifs Soustraction Relatifs Addition et soustraction de trois relatifs Produit Deux Relatifs Produit Trois Relatifs Quotient Relatifs Carré Entier Racine Carrée Théorème Pythagore Liste Diviseurs Décomposition Facteurs Premiers Calcul du PGCD PGCD Algorithme Euclide Test Nombre Premier Déterminer Fonction Linéaire Déterminer Fonction Affine Traceur Courbe Trigonométrie Angle Trigonométrie Longueur Périmètre d'un Cercle Aire d'un Disque Volume du Parallélépipède Rectangle Volume du cylindre Surface d'une Sphère et Volume d'une boule Volume d'une pyramide à base rectangulaire Section d'une pyramide Visualiser Section Cône en 2D Section d'un Cône Carte Mondiale Coordonnées Géographiques

Mathématiques Web c'est 2 250 275 fiches de cours et d'exercices téléchargées.