Exponentielle : exercices de maths en terminal corrigés en PDF.

La fonction exponentielle à travers des exercices de maths en 1ère corrigés qui vous feront progresser.

Ces énoncés font intervenir les notions suivantes :

définition de l’exponentielle;
sens de variation de la fonction exponentielle;
dérivée de la fonction exponentielle;
limites de la fonction exponentielle;
résoudre des équations et inéquations;
courbe de Gauss;
simplifier des exponentielles à l’aide des formules algébriques.

L’élève devra être capable d’effectuer des calcul avec l’exponentielle en appliquant les différentes propriétés et les formulés à connaître par cœur. Étudier des fonctions contenant des exponentielles en sachant dériver et étudier le sens de variation en créant son tableau de signe et de variations. Ces énoncés sont accompagnés de leur correction afin de vous permettre de combler vos lacunes et d’effacer vos erreurs en première.

Exercice 1 :

Ecrire à l’aide d’une seule exponentielle :

a. $\frac{1}{e^3}$

b. $e^{-2}\times e^7$

Exercice 2 :

f est une fonction dérivable sur $\mathbb{R}$ telle que $f'=f\,\,et\,\,f(0)=-\frac{1}{2}$ .

g est la fonction définie sur $\mathbb{R}$ par .

Vérifier que g est dérivable sur $\mathbb{R}$ et que g’ = g.
Calculer g(0); en déduire l’expression de g(x).
En déduire l’expression de f(x).

Exercice 3 :

Dans chaque cas, écrire l’expression avec une seule exponentielle.

a. $e^4\times e^6$

b. $e\times (e^5)^2$

c. $\frac{e^{30}\times e^{-10}}{e^{10}}$

2. a désigne un nombre réel, simplifier l’écriture de chaque expression :

$a)\,\,\frac{e^{2a}\times e^{-a}}{e^{5a}}\,\,;b)\,\,\frac{e^{2a}+1}{e^{1-a}}\,\,;\,\,c)(e^a)^3\times e$

Exercice 4 :

f est la fonction définie sur $]-1;+\infty[$ par $f(x)=\frac{e^x}{1+x}$ .

Dans un repère, $\xi$ est la courbe représentative de la fonction f et est la tangente à $\xi$ au point A d’abscisse a avec .

1. donner une équation de .

2. Démontrer qu’il existe deux valeurs de a pour lesquelles passe par l’origine du repère.

Exercice 5 :

On modélise la température moyenne T à l’intérieur d’un congélateur en posant :

$T(t)=19,5e^{-7\times 10^{-4}t}-10,5$ où $t\in[0;+\infty[$ correspond au temps, exprimé en minutes, écoulé

depuis sa mise en marche et T(t) sa température en °C.

1. Donner la température moyenne à l’intérieur du congélateur :

a. avant sa mise en marche;

b. après une journée de fonctionnement.

2. Etudier la limite de T en $+\infty$ et interpréter le résultat obtenu.

Exercice 6 :

Ecrire les réels donnés sous la forme exponentielle où k est un entier.

$1)e^{-7}\times e^3$

$2)e^{-1}\times e^{-5}$

$3)e^2 \times e$

$4)e\times e^{-1}$

$5)\frac{1}{e}$

$6)\frac{1}{e^{-1}}$

$7)\frac{1}{e^2}$

$8)\frac{1}{e^{-3}}$

$9)\frac{e^{-3}}{e^2}$

$10)\frac{e}{e^{-1}}$

$11)\frac{e^{-2}}{e}$

$12)\frac{e^2\times e^{-3}}{e^5}$

$15)(e^{-1})^6$

$16)e\times (e^{-1})^3$

Exercice 7 :

Ecrire l’expression donnée sous la forme où A est une expression.

$1)e^x \times e^2$

$2)e^{-1}\times e^{-x}$

$3)e\times e^x$

$4)e^x\times e^x$

$5)e^x\times e^{-x}$

$6)e^{x-1}\times e^x$

$8)(e^{-x+1})^3$

$10)\frac{e^{5x}}{e^x}$

$11)\frac{e^{x+1}}{e}$

$12)\frac{e^3}{e^{2x-1}}$

Exercice 8 :

On donne l’expression de trois fonctions f,g et h définies et dérivables sur $\mathbb{R}$ .

Calculer la dérivée des fonctions f, g et h.

$1)f(x)=e^{0,5x};g(x)=e^{3x};h(x)=e^{-x}$ .

$2)f(x)=e^{x+1};g(x)=e^{1-2x};h(x)=e^{-3x+1}$

$3)f(x)=2+e^{2x};g(x)=1-e^{-2x};h(x)=e^{-3x+1}$

$4)f(x)=2+e^{2x};g(x)=1-e^{-2x};h(x)=1+2e^{-x}$

Exercice 9 :

On estime que les futures découvertes de pétrole dans le monde peuvent être modélisées,
à partir de 2015, par la fonction f définie sur [15 ; + $\infty$ [ par:

$f(x)=17280e^{-0,024x}$

où f(x) représente, en millions de barils, l’estimation de la quantité
de pétrole qui sera découverte au cours de l’année 2000 + x.
1. Déterminer la limite de la fonction f en + $\infty$ .

2. Calculer f ‘ (x) et en déduire le sens de variation de la fonction f sur l’intervalle [15 ; + $\infty$ [.
3. Interpréter les résultats des questions 1 et 2.

Exercice 10:

Soit f la fonction définie sur $\mathbb{R}$ par .

Exprimer en fonction de x.

2) Justifier que, pour tout réel x de l’intervalle $[0;+\infty[$ , $f'(x)\leq\, 0$ .

3) En déduire les variations de la fonction f sur $\mathbb{R}$ .

Exercice 11 :

Ecrire les expressions suivantes sous la forme exponentielle , où A est une expression.

$1)\frac{e^{2x+1}}{e^{1-x}}$

$2)\frac{e^{-x+2}\times e^{-2x-1}}{e^{3x+2}\times e^{-x-1}}$

$3)\frac{(e^{-x})^2\times e^{-x+1}}{e^{x+2}\times (e^{-x-1})^3}$

Exercice 12 :

Démontrer les égalités suivantes :

Pour tout réel x, $-2e^{2x}+3e^x+2=(1-2e^x)(2-e^x)$ .

Pour tout réel x, $\frac{e\times e^x}{e^{2+3x}}=(e^{-x-0,5})^2$ .

Pour tout réel x, $\frac{e^{1-3x}}{1+e^{-3x}}=\frac{e}{e^{3x}+1}$

Exercice 13 :

1)Démontrer que l’équation $e^x-2e^{-x}+1=0$ est équivalente à l’équation .

2)Résoudre dans $\mathbb{R}$ l’équation $e^x-2e^{-x}+1=0$ .

Exercice 14 :

1)Résoudre dans $\mathbb{R}$ l’inéquation $e^{-x}-e^x>0$ .

2)En déduire le signe de $1-\frac{1+e^x}{1+e^{-x}}$ sur $\mathbb{R}$ .

Exercice 15 :

Soit f la fonction définie sur $\mathbb{R}^*$ par $f(x)=\frac{e^x+1}{x}$

et g la fonction définie sur $\mathbb{R}$ par $g(x)=\frac{x+1}{e^x}$ .

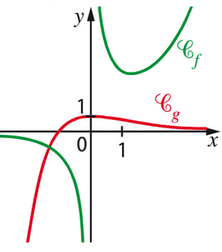
On donne ci-dessous les courbes représentatives et des fonctions f et g.

Conjecturer les limites des fonctions f et g aux bornes de leur ensemble de définition.
Démontrer ces conjectures.

Exercice 16 :

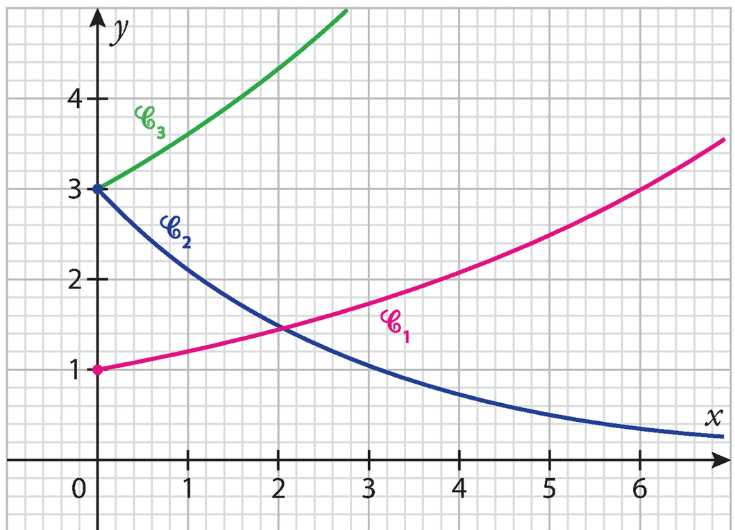
On considère les fonctions f, g et h dont les courbes sont tracées dans le repère ci-dessous.
Elles sont définies sur $\mathbb{R}^{+}$ par :

$f(x)=3\times 0,7^x$
$g(x)=3\times 1,2^x$

Associer chaque fonction à sa courbe représentative.

Exercice 17 :

f est une fonction de la forme $x \mapsto k\times a^x$ , dont on donne la représentation graphique dans le repère
ci-dessous.

Déterminer les valeurs de k et de a.

Exercice 18 :

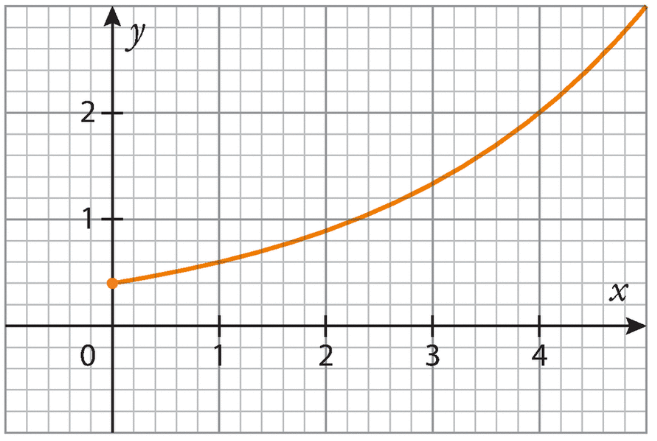
f est une fonction de la forme $x \mapsto k\times a^x$ , définie sur $\mathbb{R}^{+}$ .

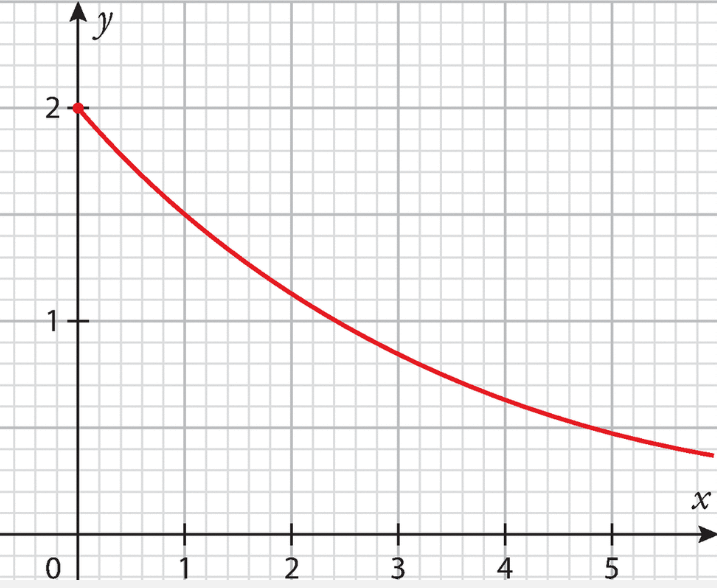
Sa courbe représentative est donnée dans le repère ci-dessous.

1.Déterminer graphiquement f(0) et f(l ).
2.En déduire les valeurs de k et de a.

Exercice 19 :
Le nombre de bactéries d’un échantillon de laboratoire augmente de 50 % chaque jour.

On suppose que l’échantillon contient 2 000 bactéries le premier jour, et on note le nombre de bactéries (en milliers) présentes au bout de n jours.

Ainsi, .
a) Donner la nature de la suite .
b) Donner le terme général de la suite .
c) En calculant les premiers termes de la suite, déterminer
au bout de combien de jours la population de bactérie dépassera 10 000.
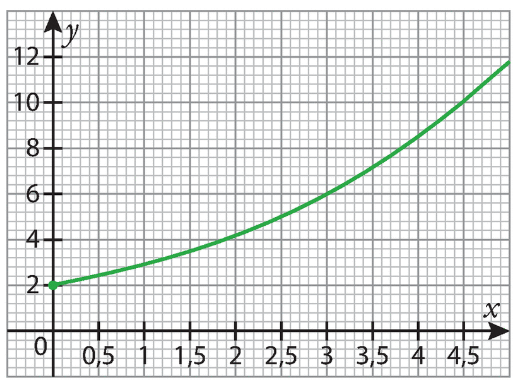
2. On a représenté dans le graphique ci-dessous la courbe
de la fonction f définie sur $[0;+\infty[$ par $f(x) = 2 \times 1,5^x$ .

a. En utilisant la courbe représentative de la fonction f, retrouver le résultat de la question 1 c).
b. Déterminer le nombre de bactéries au bout de 12 h.

3.7/5 - (4 votes)

Télécharger puis imprimer cette fiche en PDF.

Télécharger ou imprimer cette fiche «exponentielle : exercices de maths en 1ère corrigés en PDF.» au format PDF afin de pouvoir travailler en totale autonomie.

D'autres cours et exercices à consulter

Mathématiques Web c'est 2 268 522 fiches de cours et d'exercices téléchargées.