Logarithmes : exercices de maths en terminale corrigés en PDF.

Les logarithmes avec des exercices de maths en terminale corrigés font intervenir plusieurs propriétés intéressantes ainsi que les fonctions.

Ces énoncés sur les logarithmes font intervenir les notions suivantes :

définition du logarithme;
équations fonctionnelles;
formules algébriques sur les logarithmes;
limites et fonctions logarithmes.

L ‘élève devra être capable de calculer dès expression contenant des logarithme népériens en utilisant les formulés et les différentes propriétés. Étudier la fonction dérivée ainsi que des limites afin de combler vos lacunes et progresser en terminale.

Exercice 1 :

Résoudre les équations suivantes :

$a)e^x=1\\b)e^x=4\\c)e^{2x}=2\\d)4e^{-x}-3=12\\e)e^{2x-1}=2\\f)e^{-x}=-5$

Exercice 2 :

Résoudre les équations suivantes :

$a)lnx=3\\b)ln(2x)=0\\c)2lnx-1=6\\d)ln(2x-1)=3\\e)ln\,(\,\frac{1}{x-1}\,)=1\,\\f)ln(x^2)=4$

Exercice 3 :

Simplifier l’écriture des nombres suivants :

$a=ln3+ln\frac{1}{3}\\b=ln\frac{1}{16}\\c=\frac{1}{2}ln\sqrt{2}$

Exercice 4 :

Après avoir préciser l’ensemble de définition des solutions de l’équation, la résoudre.

$a)ln(1-x)+ln(1+x)=2(ln2-ln5)\\b)lnx+ln(x-3)=ln4\\c)ln(x(x-3))=ln4$

Exercice 5 :
Soit la fonction f définie sur $]0;+\infty[$ par : $f(x)=2x-1+ln\,(\,\frac{x}{x+1}\,\,)$ .
On note sa représentation graphique dans un repère orthonormé $\,(\,O;\vec{i},\vec{j}\,\,)$ du plan (unité graphique : 2 cm).
1. Étudier la limite de f en 0. Interpréter graphiquement ce résultat.
2. a. Étudier la limite de f en $+\infty$ .
b. Démontrer que la droite $\Delta$ d’équation est une asymptote à en $+\infty$ .
Étudier la position de par rapport à $\Delta$ .
3. Étudier les variations de f. Dresser son tableau de variations.
4. Démontrer que l’équation f(x) = 0 admet une unique solution $\alpha$ dans l’intervalle $]0;+\infty[$ et déterminer un encadrement de $\alpha$ d’amplitude $10^{-2}$ .
5. Tracer la droite $\Delta$ et la courbe .

Exercice 6 :

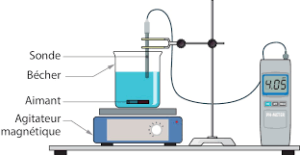
Utile aussi pour le bac… en Chimie !
On sait, en Chimie, que le pH d’une solution permet d’exprimer son caractère acide ou basique.
Ce nombre est un décimal compris entre 1 et 14 de sorte que :
● Si pH < 7, alors la solution est dite acide.
● Si pH > 7, alors la solution est dite basique.
● Si pH = 7, elle est dite neutre.

On sait alors que le pH est associé à la relation $pH\,=\,-\,log[H_3O^{+}]$ où est la concentration en ions , exprimée en mol/L.

1. Une solution possède une concentration en ions égale à $5\times \,10^{-9}$ .
Quel est son pH ? Que peut-on dire d’une solution dont la concentration en ions est
égale à 0,1 ?
2. Quelle est la concentration en ions d’une solution neutre ?
3. Si l’on augmente la concentration en ions dans une solution, diminue-t-on ou augmente-t-on le pH de cette solution ?
4. Que faut-il faire à une solution pour incrémenter ou décrémenter son pH ?

Vocabulaire : Incrémenter, c’est ajouter 1. Donc décrémenter, c’est… ?

Exercice 7 :
f est la fonction définie sur $\mathbb{R}$ par :
$f(x)=x+2-ln(1+e^{2x})$ .
C est sa courbe dans un repère orthogonal $\,(\,O;\vec{i},\vec{j}\,\,)$ .

1. a. Déterminer la limite de $ln(1+e^{2x})$ en $-\infty$ .
b. En déduire l’existence d’une asymptote oblique $\Delta$ dont on précisera une équation.
c. Montrer que pour tout réel x :
$f(x)=2-x-ln(1+e^{-2x})$
d. Déterminer la limite de f en $+\infty$ , ainsi que l’existence d’une seconde asymptote oblique
$\Delta'$ .
2. Montrer que l’axe des ordonnées est un axe de symétrie pour C.
3. Résoudre l’inéquation $1-e^{2x}\,\geq\,\,0$ .
4. Étudier les variations de la fonction f.
5. Représenter $\Delta$ , $\Delta'$ et C, après avoir indiqué la position de $\Delta$ et C.

Exercice 8 :

La température $\theta$ (en °C) d’un liquide peut être modélisée en fonction du temps t, en min, par :
$\theta\,(t)\,=\,25\,-10e^{0,1t}$
Donner les réponses arrondies au dixième.
a) Au bout de combien de temps la température atteindra-t-elle 12,5 °C ?
b) Au bout de combien de temps la température atteindra-t-elle 0°C ?

Exercice 9 :

A l’aide de la calculatrice, on a affiché la courbe représentative de la fonction f définie sur $]0;+\infty[$ par
$f(x)=(ln(x)\,-1)(3\,-ln(x))$

a) Déterminer l’abscisse de chacun des points d’intersection de cette courbe avec l’axe des abscisses.
b) Étudier le signe de la fonction f sur $]0;+\infty[$ .

Exercice 10 :

Résoudre les équations suivantes :

a) $a)ln(9x)+ln(x)=25\\b)ln(x+4)+ln(2x-1)=ln(x+10)\\c)2ln(x)=ln(x+4)+ln(2x)\\d)ln(x^2)=ln(2x^2+8x)$

$e)ln(x-2)-ln(x-3)=1\\f)ln(2x-3)-2ln(x+1)=ln(x-3)\\g)ln(x)-ln(x+1)=ln(x-1)\\h)ln(5-x)-ln3+ln(x-1)=0$

Exercice 11 :

f est la fonction définie sur $]0;+\infty[$ par :

1.Étudier la limite de f en 0.
2.a) Vérifier que l’étude de la limite de f en $+\infty$ conduit à une forme indéterminée.
b) Pour tout $x\,>\,0,\,f(x)\,=\,ln(x)\,(ln(x)-1)$
En déduire la limite de f en $+\infty$ .

Exercice 12 :

g est la fonction définie sur $]1;+\infty[$ par :
$g(x)=\frac{3\,+\,ln(x)}{ln(x)}$
a) Quel est le signe de ln(x) lorsque $x>\,1$ ?
b) En déduire la limite de g en 1.
2. Expliquer pourquoi pour tout réel $x\,>\,1,\,g(x)=\frac{3}{ln(x)}+1$

En déduire la limite de g en $+\infty$ .

Exercice 13 :

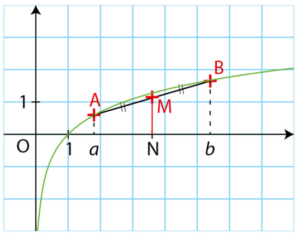
Dans un repère orthonormé, A et B sont deux points de la courbe représentative de la
fonction d’abscisses respectives a et b.
M est le milieu du segment [AB] et N est le projeté orthogonal de M sur l’axe des
abscisses.
Démontrer que $MN=ln(\sqrt{ab})$ .

Exercice 14 :

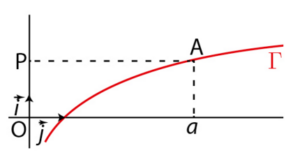
a désigne un nombre réel strictement positif. On note A le point d’abscisse a
de la courbe représentative de la fonction logarithme népérien dans un repère orthonormé $(O;\,\vec{i},\,\vec{j})$ .
P est le projeté orthogonal du point A sur l’axe des ordonnées.
a) Q est le point d’intersection de la tangente T au point A à la courbe $\Gamma$ ‘ et de l’axe des ordonnées.
Calculer la longueur PQ.
b) En déduire une construction simple de la tangente T.

Exercice 15 :

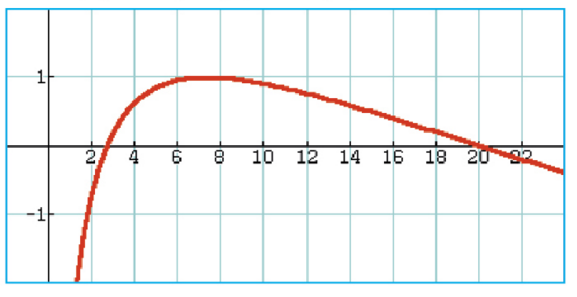
1.f est une fonction définie sur $]0;+\infty[$ par $f\,(x)\,=\,ax\,+\,(bx\,+\,c)ln(x)$
où a, b, c sont des réels.
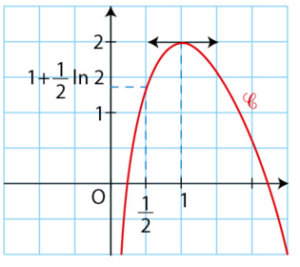
La courbe représentative $\varphi$ de f est donnée ci-dessous.
Utiliser les informations données sur le graphique pour déterminer a, b, c.

2. g est la fonction définie sur $]0;+\infty[$ par $g(x)\,=\,2x+\,(1-\,3x)ln(x).$

a) Étudier la limite de g en 0, puis en $+\infty$ .
b) Déterminer la fonction dérivée de g et étudier son signe en remarquant que $\frac{1-x}{x}$
et -3ln(x) ont le même signe sur ]0 ; 1 [et sur $]1;+\infty[$ .
c) Dresser le tableau de variations de g.

Exercice 16 :

Le gain, en décibel (dB), d’une antenne parabolique de 1 m de diamètre peut se calculer par la formule :
G = 20 x 10 90
où f est la fréquence d’utilisation, en hertz (Hz).
a) Calculer le gain de l’antenne pour une fréquence d’utilisation de $9\,\times \,10^9$ Hz.

Arrondir au centième.
b) A partir de quelle fréquence peut-on utiliser une telle antenne sachant que le gain doit être supérieur
ou égal à 20 dB ? Arrondir à 10^7 Hz.

Exercice 17 :

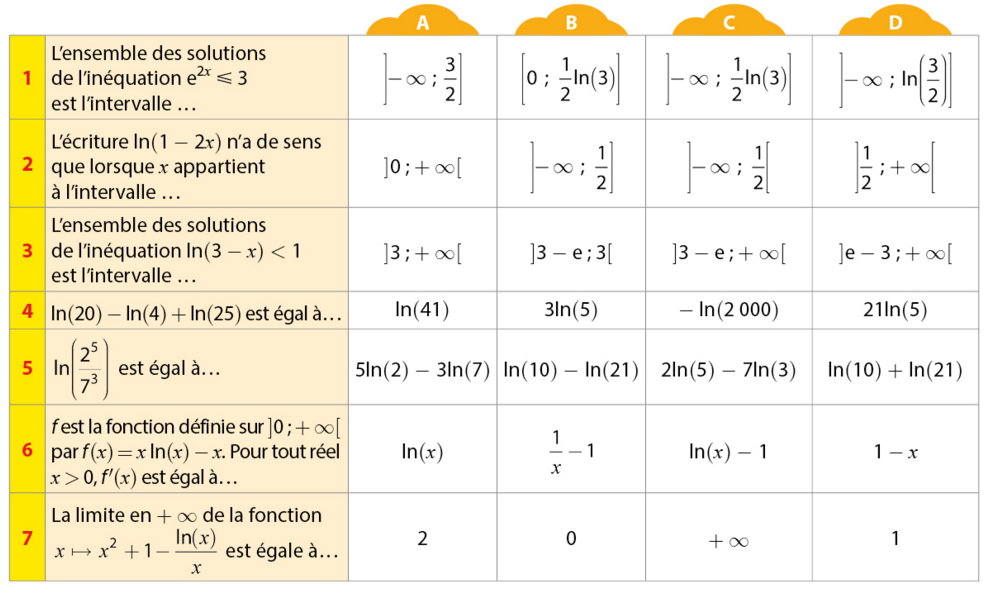
Effectuer les QCM sur les fonctions logarithmes suivants :

Exercice 18 :

Dans chaque cas, donner la (ou les) réponse(s) exacte(s) sans justifier.

Voir Exercices 11 à 18...

Télécharger puis imprimer cette fiche en PDF.

Télécharger ou imprimer cette fiche «logarithme : exercices de maths en terminale corrigés en PDF.» au format PDF afin de pouvoir travailler en totale autonomie.

Vous devez vous inscrire ou vous connecter à votre compte afin de pouvoir télécharger ce document au format PDF.

Réviser les cours et exercices avec nos Q.C.M :

Q.C.M en 6ème Q.C.M en 5ème Q.C.M en 4ème Q.C.M en 3ème Q.C.M en 2de Q.C.M en 1ère Q.C.M en Terminale

D'autres ressources pour progresser en autonomie :

Chronomètre Horloge France Tables Multiplication Arrondir des décimaux Rapporteur et Angles Médiatrice Symétrie Axiale d'un triangle Symétrie Centrale d'un triangle Translation d'un triangle Rotation Homothétie Bissectrice Tracer droite parallèle Conversion Aires et Volumes Addition de deux relatifs Soustraction Relatifs Addition et soustraction de trois relatifs Produit Deux Relatifs Produit Trois Relatifs Quotient Relatifs Carré Entier Racine Carrée Théorème Pythagore Liste Diviseurs Décomposition Facteurs Premiers Calcul du PGCD PGCD Algorithme Euclide Test Nombre Premier Déterminer Fonction Linéaire Déterminer Fonction Affine Traceur Courbe Trigonométrie Angle Trigonométrie Longueur Périmètre d'un Cercle Aire d'un Disque Volume du Parallélépipède Rectangle Volume du cylindre Surface d'une Sphère et Volume d'une boule Volume d'une pyramide à base rectangulaire Section d'une pyramide Visualiser Section Cône en 2D Section d'un Cône Carte Mondiale Coordonnées Géographiques

Mathématiques Web c'est 2 253 856 fiches de cours et d'exercices téléchargées.