Fonctions linéaires : exercices de maths en 3ème corrigés en PDF.

D'autres cours et exercices à consulter

Les fonctions linéaires avec une série d’exercices de maths en 3ème corrigés afin de progresser dans la matière.

Vous retrouverez dans ces énoncés avec les notions suivantes :

calcul d’une image;
calcul d’antécédent;
calcul du coefficient directeur;
tracé de la courbe d’une fonction linéaire;
calcul de pourcentages (augmentation et réduction).

Ces énoncés sont corrigés et peuvent être imprimés en ˋPDF.

Exercice 1

Compléter le tableau suivant donnant les images des nombres –1,5 , – $\frac{1}{2}$ , 0 , 1, $\frac{3}{4}$ , et 2 par chacune des applications linéaires proposées.

Exercice 2

Indiquer pour chacun des tableaux, s’il s’agit d’un tableau de proportionnalité et, si c’est le cas, exprimer l’application linéaire associée, traduisant la correspondance entre la première et la seconde ligne.

Tableau 1				Tableau 3
5	10	15	20	1,5	2	2,5	3
10	15	20	25	4,5	6	7,5	9
Tableau 2				Tableau 4
30	33	36	39	7	14	21	35
10	11	12	13	1	2	3	4

Exercice 3

Dans chacun des cas, on connaît un nombre et son image par une application linéaire. Déterminer son coefficient et l’exprimer sous la forme la plus simple possible.

8 $\mapsto$ – 64	9 $\mapsto$ 6	7 $\mapsto$ 4,9	11 $\mapsto$ -32
0,3 $\mapsto$ 12	1,2 $\mapsto$ 0,4	– 2,5 $\mapsto$ – 8	25 $\mapsto$ – 5

Exercice 4

Compléter les tableaux de valeurs des applications linéaires en utilisant les propriétés de la linéarité.

Application 1					Application 2
3	36	18	4	-2	2	4	-4	10
		63				5			-15

Exercice 5

Donner les applications linéaires associées aux situations suivantes utilisant des pourcentages :

Augmenter de 25%
Diminuer de 20%
Diminuer de 4%
Augmenter de 10%
Diminuer de 75%

Exercice 6

Traduire chacune de ces applications linéaires par une variation en pourcentage :

x $\mapsto$ 1,35x	x $\mapsto$ 0,98x	x $\mapsto$ 3/2 x	x $\mapsto$ ¾ x	x $\mapsto$ 1,01 x
x $\mapsto$ 0,86x	x $\mapsto$ 1,31x	x $\mapsto$ 4/9 x	x $\mapsto$ 5/8 x	x $\mapsto$ 1,002x

Exercice 7

Les points suivants dont on donne les cordonnées sont-ils situés sur la droite représentant graphiquement l’application linéaire x $\mapsto$ – 0,75x ?

A (-1 ; 0,75) B (-2 ; $\frac{3}{2}$ ) C (-0,2 ; – 0,15) D (- $\frac{4}{3}$ ; 1)

Exercice 8

Dans un même repère représenter graphiquement les applications linéaires définies par :

x $\mapsto$ x ; x $\mapsto$ – x ; x $\mapsto$ – 3x ; x $\mapsto$ – $\frac{3}{2}$ x

Exercice 9

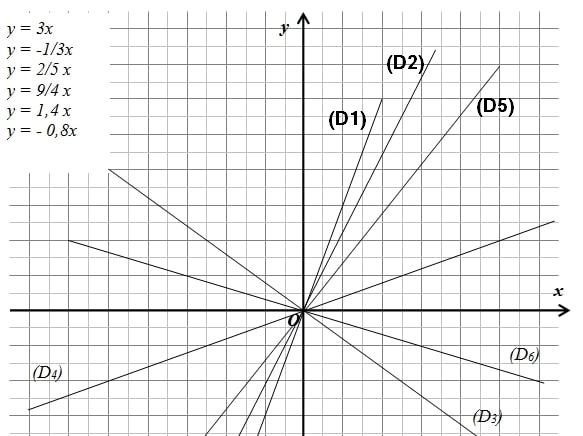
Associer chacune des droites représentées à l’une des applications linéaires proposées.

Exercice 10

Tracer dans un repère orthonormé du plan, les représentations graphiques des fonctions linéaires et donner une équation de ces quatre droites.

f₁: x $\mapsto$ 3x f₂: x $\mapsto$ -3x f₃: x $\mapsto$ 2,5x f₄: x $\mapsto$ – x
Tracer la droite d’équation y = $\frac{5}{3}$ x.

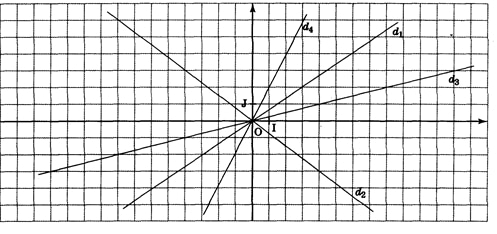
Exercice 11

Les droites d₁ , d₂ , d₃ , d₄ sont les représentations graphiques des fonctions linéaires f₁ , f₂ , f₃ , f₄.

Déterminer les coefficients de ces fonctions puis donner les expressions algébriques de ces fonctions

f₁(x) = ……… f₂(x) = ……… f₃(x) = ……… f₄(x) = …………

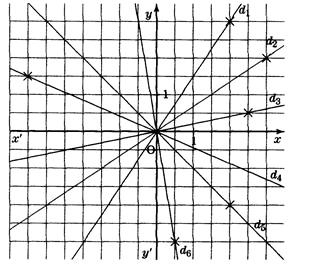
Exercice 12

Relever les coordonnées du point marqué.
Trouver le coefficient de la fonction linéaire
Donner l’expression algébrique de cette fonction.

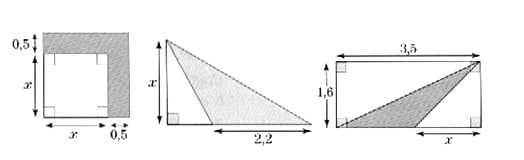
Exercice 13

Dans chacun des cas suivants, exprimer l’aire A(x) de la surface coloriée en fonction de x.

Préciser si x $\mapsto$ A(x) est linéaire

Exercice 14

Vente de tomates .

Prix au kilo : 2 € .

Proportionnalité :

1. Montrer que le prix payé y (en €) est proportionnel à la masse de tomates x (en kg) achetée.

2. Etablir la relation entre y et x .

3. Le coefficient de proportionnalité est a = ….. .

Ces deux grandeurs étant proportionnelles, le prix payé est donc une fonction linéaire de la masse de tomates achetée.

Etude de la fonction linéaire :

Soit la fonction linéaire, notée

f : x $\mapsto$ f(x)

(masse de tomates ® prix payé)

Quelle est la relation entre f(x) et x ?

f(x) =………

Justifier le fait que f est une fonction linéaire .

Calculer f(3) ; f(0) ; f( 5) .

Calculer l’image de 7 par la fonction f .
Quelle est la signification concrète du résultat ?
Quel est le nombre ayant pour image 5 ?

(f : ? $\mapsto$ 5 )

7. Quel est le nombre ayant pour image 6,5 ?

(f : ? $\mapsto$ 6,5 )

8. Compléter le tableau suivant à l’aide des résultats précédents :

x	0		3		5	7
f(x)		5		6,5
Points	O		A		B	C

9. Dans un repère orthogonal, représenter la courbe de la fonction f .

Unités graphiques :

· Abscisses : 1 cm $\mapsto$ 1 kg .
· Ordonnées : 1 cm $\mapsto$ 2 € .

9. Déterminer graphiquement :

(laisser les traits de construction apparents)

· Le prix de 3,5 kg de tomates ;

· La masse de tomates achetée pour 8 euros .

Exercice 15

f est la fonction linéaire définie par

a. Calculer l’image de 3 par f.
b. Déterminer l’antécédent de -4 par f.
2. Dans un repère, tracer la droite (d) représentant graphiquement la fonction f.

Exercice 16
est la fonction linéaire définie par .

a. Calculer .
b. Déterminer l’antécédent de 19 par la fonction t.
c. Dans un repère, tracer la droite (d) représentant
graphiquement la fonction t.

Exercice 17

Exercice 18

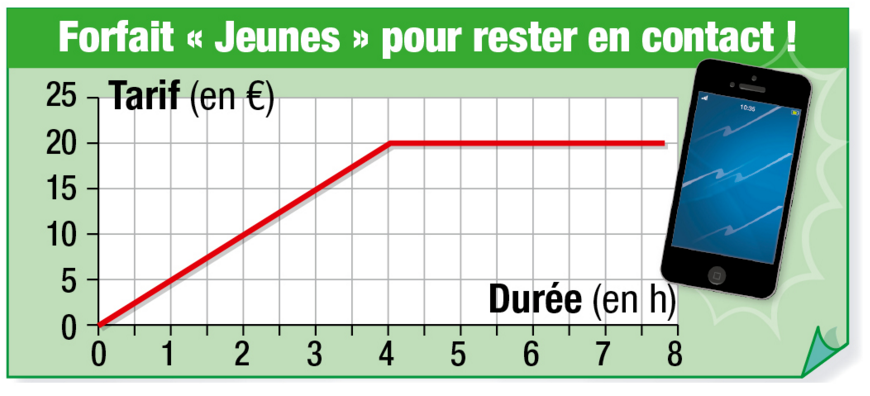
Voici une publicité pour un forfait de téléphone.

a. Le tarif est-il proportionnel la durée ? Justifier.
b. Décrire ce forfait de téléphone par une phrase

Exercice 19

h est la fonction linéaire : $h:x \mapsto - 3,2x$ .
Recopier et compléter le tableau.

Exercice 20

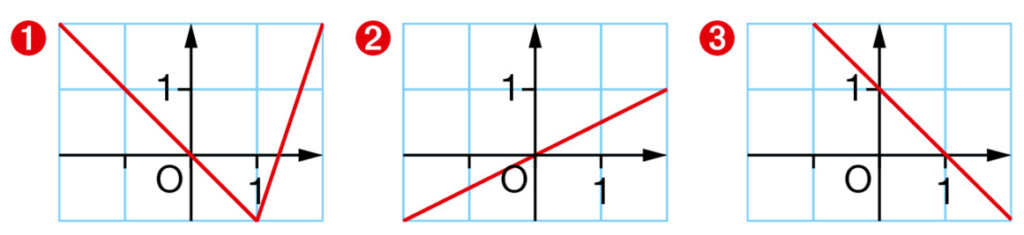
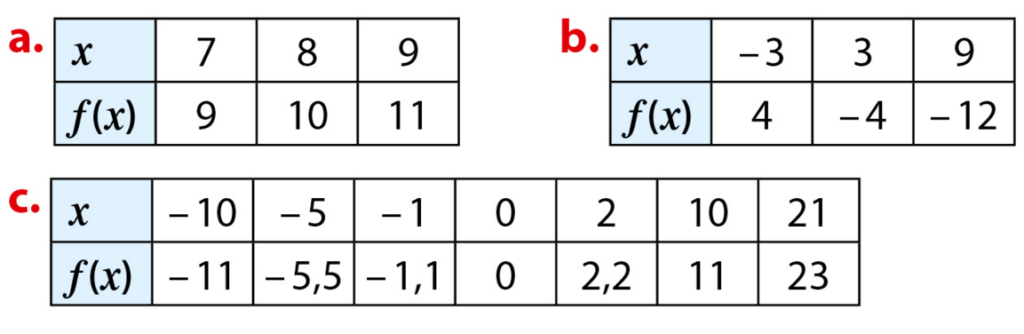
Dans chaque cas, dire si la fonction f peut être linéaire.

Si oui, donner son coefficient.

Exercice 21

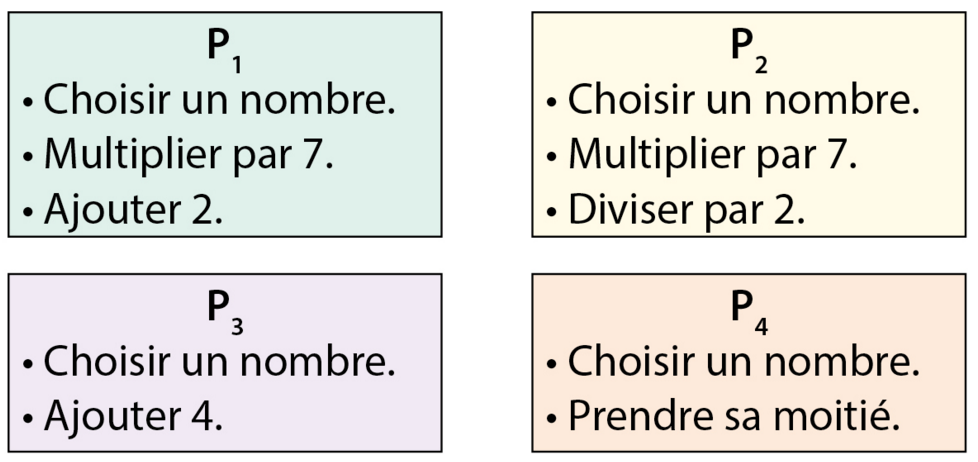
Pour chaque programme de calcul, dire si l’on peut lui associer une fonction linéaire.
Si oui, donner son coefficient.

4.3/5 - (6 votes)

Télécharger puis imprimer cette fiche en PDF.

Télécharger ou imprimer cette fiche «fonctions linéaires : exercices de maths en 3ème corrigés en PDF.» au format PDF afin de pouvoir travailler en totale autonomie.

– $\frac{1}{2}$

$\frac{3}{4}$

x $\mapsto$ 3x

X $\mapsto$ -2x

X $\mapsto$ $\frac{ 1}{4}$ x

X $\mapsto$ – $\frac{3}{4}$ x

X $\mapsto$ 0,3x

Mathématiques Web c'est 2 268 028 fiches de cours et d'exercices téléchargées.