Corrigé des exercices sur le théorème de Thalès en 3ème.

Le théorème de Thalès en maths est très intéressant mais aussi pratique. Il vous permet de résoudre vos exercices tout en développant des compétences.

Exercice 1 :

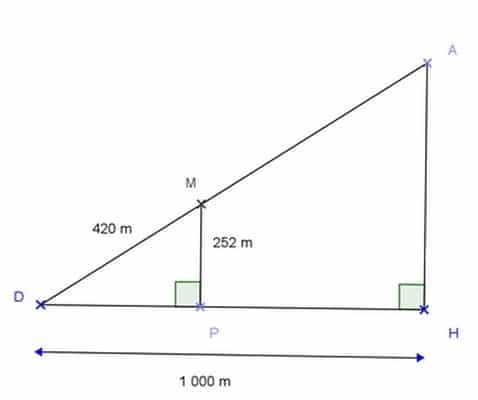
Un funiculaire part de D pour se rendre à A suivant la droite (DA) .

DM = 420 m ;  DH = 1 000 m;

MP = 252 m.

Les triangles DPM et DAH sont respectivement rectangles en P et H.

1) Calculer la distance DP en mètre.

Dans le triangle DMP rectangle en P, d’après la partie directe du théorème de Pythagore, nous avons l’égalité suivante :

2) a) Démontrer que les droites (MP) et (HA) sont parallèles.

On sait que :

(MP) est perpendiculaire à (DH)

(AH) est perpendiculaire à (DH)

Propriété :

Deux droites perpendiculaires à une même troisième sont parallèles entre elles

Conclusion : (MP) //(HA)

b) Calculer la distance DA en mètre puis en kilomètre.

On sait que :

d’après la partie directe du théorème de Thalès, nous avons les égalitéés suivantes :

donc

Exercice 7 :

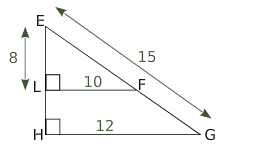
1.Démontrer que les droites (LF) et (HG) sont parallèles.

On sait que 

Propriété : deux droites perpendiculaires à une même troisième sont parallèles entre elles.

Conclusion : (LF)//(HG).

2.Calculer EF, EH et FG.

On sait que : 

D’après la partie directe du théorème de Thalès, nous avons les égalités suivantes :

donc

  et

Exercice 8 :

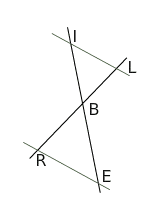
Sur la figure ci-dessous, BR=2,5 cm, BL=15cm, BE=1,5 cm et BI = 9 cm.

Les points I,B et E sont alignés dans le même ordre que L,B,R.

Montrer que les droites (IL) et (ER) sont parallèles.

On sait que les points I,B et E sont alignés dans le même ordre que L,B,R.

Calculons séparément :

    et

or   et .

Nous pouvons en déduire que  et d’après la réciproque du théorème de Thalès,

les droites  (IL) et (ER) sont parallèles.

[expander_maker id= »1″ more= »Voir Corrigés 11 à 15… » less= »Fermer ce Bloc »]

Exercice 14 :

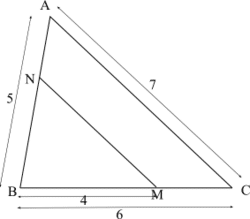
Les droites (NM) et (AC) sont parallèles et les longueurs sont exprimées en cm.

Calculer la valeur de NM (donner la valeur exacte et la valeur approchée au millimètre).

On sait que (NM)//(AC),  d’après la partie directe du théorème de Thalès,

nous avons les égalités suivantes :

en utilisant la règle du produit en croix :

Exercice 15 :

Les droites (AD) et (CE) sont parallèles.

Calculer la valeur de CE (donner la valeur exacte et la valeur approchée au millimètre)

On sait que (AD)//(CE),  d’après la partie directe du théorème de Thalès,

nous avons les égalités suivantes :

[/expander_maker]