Suites : exercices de maths en terminale corrigés en PDF.

Les suites numériques à travers des exercices de maths en terminale corrigés et qui vous permettront de réviser le chapitre.

Cette fiche fait intervenir les notions suivantes :

définition d’une suite;
somme des termes d’une suite;
convergence d’une suite numérique;
comportement asymptotique d’une suite;
étude suite et fonctions;
suites récurrentes.

L’élève devra être capable de calculer des termes de rang n ou de déterminer la somme de ses premiers termes. Étudier le sens de variation et la convergence ainsi que, déterminer son éventuelle limite en l’infini.

Ces énoncées sont accompagnés de leur correction afin de vous permettre de pointer vos erreurs commises en terminale.

Exercice n° 1 :

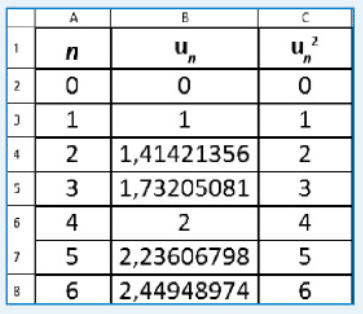
u est la suite définie par et, pour tout nombre entier naturel n, $u_{n+1}=\sqrt{u_n^2+1}$ .

Avec le tableur, on a obtenu ci-dessous les premières valeurs de et .

Conjecturer une expression de en fonction de n.
Valider cette conjecture par un raisonnement par récurrence.

Exercice n° 2 :

V est la suite définie par et pour tout nombre entier naturel n, $V_{n+1}=V_n+2n+2$ .

Démontrer par récurrence que pour tout nombre entier naturel n, .

Exercice n° 3 :

Montrer par récurrence que, pour tout entier naturel n, $2^n\geq\, \, n+1$ .

Exercice n° 4 :

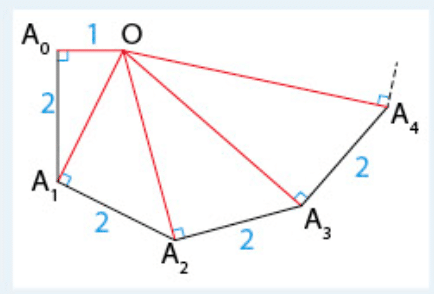
Sur cette figure :

les triangles sont rectangles.

Démontrer par récurrence, que pour tout nombre entier naturel n, $OA_n=\sqrt{4n+1}$ .

Exercice n° 5 :

Etudier, en justifiant, la limite en l’infini de chacune des suites numériques suivantes :

$1.\,u_n=3(2-0,9^n)\\2.\,v_n=1,01^n-5\\3.\,w_n=\frac{3+0,2^n}{0,9^n-5}\\4.\,t_n=\frac{4^n+5}{2\times 3^n}$

Exercice n° 6 :

u est la suite géométrique de raison 0,8 et de premier terme .

Pour tout nombre entier naturel n non nul, exprimer en fonction de n.
Etudier la limite de la suite .

Exercice n° 7 :

On considère la suite définie par et pour tout $n\in \mathbb{N}$ ,

$u_{n+1}=\frac{3u_n}{1+2u_n}$ .

1)Soit f la fonction définie sur $[0;+\infty[$ par $f(x)=\frac{3x}{1+2x}$ .

a)Etudier les variations de f sur $[0;+\infty[$ .

b) En déduire que si $x\in[0;1]$ , alors f ‘ (x) $\in[0;1]$ .

2)Démontrer par récurrence que, pour tout entier naturel n, $0\leq\, u_n\leq\, 1$ .

3)Déterminer le sens de variation de la suite .

Exercice n° 8 :

La suite est définie par et pour tout $n\in \mathbb{N}^*$ ,

$u_{n+1}=u_n+2n+1$ .

1)A l’aide de la calculatrice ou d’un tableur, déterminer les dix premiers

termes de la suite .

2)a)Quelle conjecture peut-on faire sur l’expression de en fonction de n ?

b)Démontrer cette conjecture par récurrence.

Exercice n°9 :

Montrer par récurrence que, pour tout entier naturel n non nul,

$\sum_{q=1}^{n}q^2=\frac{n(n+1)(2n+1)}{6}$ .

Exercice n° 10 :

Déterminer la limite de définie sur $\mathbb{N}^*$ en utilisant les théorèmes généraux.

$2)u_n=\frac{3}{3+2n}$ .

$3)u_n=4n-1+\frac{5}{\sqrt{n}}$ .

$4)u_n=-n^2-5n+\frac{1}{n}$

Exercice n°11 :

Soit la suite définie par et, pour tout $n\in \mathbb{N}$ ,

$u_{n+1}=-\frac{1}{3}u_n+1$ .

Soit la suite définie pour tout entier naturel n par :

1)Montrer que la suite est géométrique de raison $-\frac{1}{3}$ .

Préciser le premier terme.

2) Déterminer l’expression de en fonction de n et en déduire que,

pour tout entier naturel n :

$u_n=\frac{17}{4}\times (-\frac{1}{3})^n+\frac{3}{4}$ .

3) Déterminer la limite de la suite .

Exercice n° 12 :

Etudier si les suites suivantes, définies sur $\mathbb{N}$ , sont bornées.

$1)u_n=(\frac{1}{3})^n-8$ .

Exercice n° 13 :

est la suite définie sur $\mathbb{N}$ par :

On se propose d’étudier la limite de la suite de trois façons différentes.
a) Démontrer que pour tout n,
b) En déduire la limite de la suite .
2. Pour tout $n\geq\, 1$ , mettre en facteur dans l’expression de et conclure pour la limite de (un).
3. a) Démontrer que pour tout $n \geq\, 4$ , $u_n \geq\, 2n^2$
b) En déduire la limite de la suite .

Exercice n° 14 :

Jenny a ouvert un livret A et a déposé 5 000 €.

Les intérêts composés sont de 0,5 % par an et, en chaque fin d’année, Jenny ajoutera 100 € sur son livret.
On désigne par la somme, en euro, sur son livret A après n années, avec $n \in \mathbb{N}$ .
a) Démontrer que, pour tout n, $Jn \geq\, 5 000 + 1 00n$ .
b) En déduire la limite de la suite ().
c) Tabuler la suite () l’écran de la calculatrice et déterminer après combien d’années Jenny disposera de plus de 7 OOO €.

Exercice n° 15 :

est la suite définie par et pour tout entier naturel n, $u_{n+1}=u_n+\frac{1}{u_n}$ .
Trois amis émettent des conjectures.
Cyril affirme : « Tous les termes de la suite sont strictement positifs ».
Magali affirme : « La suite diverge vers $+\infty$ quelle que soit la valeur du premier terme ».
Olivier rétorque : « La suite peut converger si on choisit ni trop grand ni trop proche de 0 ».
a) L’affirmation de Cyril est-elle vraie ? Justifier.
b) Démontrer par récurrence que pour tout entier naturel n, $u_n^2\geq\, 2n$ .
c) L’une des affirmations de Magali et d’Olivier est-elle vraie ? Justifier.

3.6/5 - (16 votes)

Télécharger puis imprimer cette fiche en PDF.

Télécharger ou imprimer cette fiche «suites numériques : exercices de maths en terminale corrigés en PDF.» au format PDF afin de pouvoir travailler en totale autonomie.

D'autres cours et exercices à consulter

Mathématiques Web c'est 2 268 028 fiches de cours et d'exercices téléchargées.