Le triangle : exercices de maths en 5ème corrigés en PDF.

Le triangle avec des exercices de maths en 5ème corrigés . L’élève devrai être capable d’affirmer si un triangle est constructible connaissant la valeur des longueurs de ses trois côtés en utilisant l’inégalité triangulaire. Connaître la propriété de la somme des mesures des trois angles d’un triangle qui vaut 180°. Développer des compétences en géométrie avec des constructions à la règle, au compas, à l’équerre et avec le rapporteur. Nous terminerons ce chapitre sur le triangle avec le cercle circonscrit et les médiatrices.

Exercice 1 :

Soit ABC un triangle quelconque. On appelle I le milieu de [AB] et C’ le symétrique de C par rapport à I, puis J le milieu de [AC] et B’ le symétrique de B par rapport à J.

1) a) Démontrer que $\widehat{BAC}$ et $\widehat{ABC}$ ont la même mesure.
b) En reprenant exactement la même démonstration avec la symétrie de centre J, quel résultat analogue obtiendrait-on ? (on ne rédigera pas cette nouvelle démonstration et on considérera ce résultat comme acquis dans la suite de l’exercice)

2) a) Démontrer que (BC) et (AC’) sont parallèles.
b) En reprenant exactement la même démonstration avec la symétrie de centre J, quel résultat analogue obtiendrait-on ? (on ne rédigera pas cette nouvelle démonstration et on considérera ce résultat comme acquis dans la suite de l’exercice)
c) Démontrer que C, A et B’ sont alignés
3) a) Déterminer $\widehat{BAC'}$ + $\widehat{BAC}$ + $\widehat{CAB'}$
b) En déduire la somme des mesures des trois angles du triangle ABC.

Exercice 2 :
Soit ABC un triangle rectangle en A. Montrer que $\widehat{ABC}$ et $\widehat{ACB}$ sont complémentaires.

Exercice 3 :
Soit ABC un triangle tel que $\widehat{ABC}$ et $\widehat{ACB}$ soient complémentaires. Montrer que ABC est rectangle en A.

Exercice 4 :
Soit ABC un triangle isocèle en A et d la médiatrice de [BC].
1) Montrer que A appartient à d.
2) Déterminer les images de A, B et C par la symétrie d’axe d.
3) Montrer que les angles à la base du triangle ABC sont de même mesure.

Exercice 5 :
Soit ABC un triangle isocèle en A et ayant un angle de 60°.
1er cas : L’angle de 60° est (BAC) ˆ: Déterminer $\widehat{ABC}$ et $\widehat{ACB}$ . En déduire que ABC est équilatéral.
2ème cas : L’angle de 60° est $\widehat{ABC}$ : Déterminer $\widehat{ACB}$ et $\widehat{BAC}$ . En déduire que ABC est équilatéral.
3ème cas : L’angle de 60° est $\widehat{ACB}$ : Pourquoi est-il inutile d’étudier ce troisième cas ?

Exercice 6 :
Soit ABC un triangle quelconque et O le point d’intersection des médiatrices de [AB] et de [AC].
1) Montrer que OA = OB puis que OA = OC.
2) En déduire que O est le centre du cercle circonscrit au triangle.
3) En déduire également que O appartient aussi à la médiatrice de [BC].

Exercice 7 :

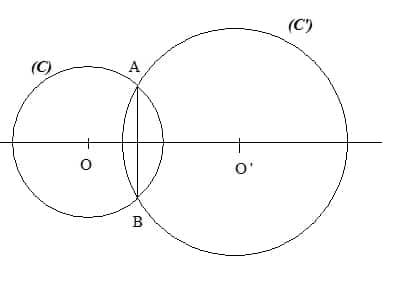
( C ) est un cercle de centre O et de rayon 2 cm.

( C’ ) est un cercle de centre O’ et de rayon 3 cm.

Les deux cercles se coupent en A et B.

Exercice 8 :
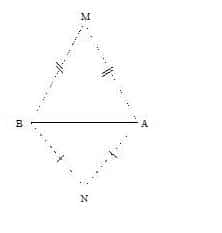
Expliquer pourquoi sur la figure ci-dessous (MN) perpendiculaire à (AB).

Exercice 9 :

Tracer un segment [AB].

Construire son milieu I sans utiliser de quadrillage ni d’instrument graduée.

Exercice 10 :

On donne une droite (d) et un point N qui n’est pas sur cette droite.

Construire deux points A et B de (d) tel que la médiatrice de [AB] passe par N.

Exercice 11 :

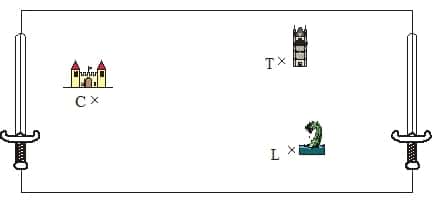
Le bon roi Gatovert a caché son épée magique.

Tu dois la retrouver sur le plan ci-dessous, sachant qu’il l’a enterrée à égale distance de son château C, de la vielle tour T et du lac au dragon L.

Exercice 12 :

a) Tracer trois points R, S et T non alignés.

Construire un point K à égale distance des trois points.

b) Comment s’appelle le point que tu as construit ? Y a-t-il plusieurs solutions ?

Exercice 13 :

a) Tracer un segment [AB] de longueur 3,8 cm.

Construire un triangle ABC sachant que côté [AC] mesure 5 cm et que le rayon du cercle circonscrit est de 3 cm.

b) Combien y a-t-il de triangles possibles ?

c) Construis-les tous.

Exercice 14 :

a) Construire les triangles EFG et MNP tels que :

· EF 8,4 cm, FG = 7,4 cm et EG = 6,3 cm ;

· MN 5,9 cm, NP = 6,5 cm et MP = 8 cm.

b) Tracer leur cercle circonscrit.

c) Quelle différence y-a-t-il entre les centres de ces deux cercles ?

Exercice 15 :

Construire à chaque fois le cercle circonscrit d’un triangle ABC :

a) AB 4,5 cm, BC 7 cm et 75°.

b) ABC est isocèle en A avec AB = 5 cm et 120°.

c) ABC est équilatéral ce côté 6 cm.

d) ABC est rectangle en A, avec AB = 5 cm et AC = 7 cm.

Exercice 16 :

On considère un triangle ABC.

On sait que $\widehat{A}$ = 28° et $\widehat{B}$ = 73°.

En déduire la mesure de C.

Exercice 17 :

Magalie a mesuré les angles $\widehat{DEF}$ avec son rapporteur.

Elle a trouvé $\widehat{D}$ = 53°, $\widehat{E}$ = 74° et $\widehat{F}$ = 54°.

Que penses-tu de sa réponse ? Justifie.

Exercice 18 :

On considère un triangle GHI, rectangle en H.

On sait que $\widehat{G}$ = 34°.

En déduire la mesure de $\widehat{I}$ .

Exercice 19 :

On considère un triangle équilatéral JKL.

En déduire la mesure de ses trois angles.

Exercice 20 :

On considère un triangle MNO, isocèle de sommet principal N et de base [MO].

On sait que $\widehat{N}$ = 44°. En déduire la mesure de $\widehat{M}$ et $\widehat{O}$ .

Exercice 21 :

On considère un triangle PQR, isocèle de sommet principal Q et de base [PR].

On sait que $\widehat{P }$ = 75°.

En déduire la mesure de $\widehat{R}$ et $\widehat{Q}$ .

Exercice 22 :

On considère un triangle STU, rectangle isocèle de sommet principal T et de base [SU].

En déduire la mesure de ses 3 angles.

Exercice 23 :

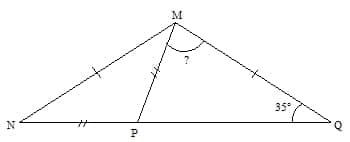
Le triangle MNQ est isocèle de sommet principal M et de base [NQ].

Le triangle PMN est isocèle de sommet principal P et de base [MN].L’angle $\widehat{MQN}$ mesure 35°.

Détermine la mesure de l’angle $\widehat{PMQ}$ .

Pour cela, on traduira la situation proposée par une équation que l’on résoudra.

Exercice 24 :
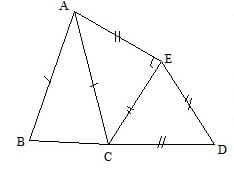
En utilisant les indications portées sur la figure, détermine les mesures de tous les angles.

Exercice 25 :

ABC est un triangle équilatéral de côté 6cm et de cercle circonscrit B.
D est un point du petit arc et E le point de [AD] tel que DE = DC. La droite (EC) coupe B en F.

1) Montrer que le triangle EDC est équilatéral.

2) Montrer que FA = FE.

3) Montrer que le quadrilatère FBDE est un parallélogramme.

Exercice 26 :

Soit un triangle AIJ tel que AI = 10 ; AJ = 17 et IJ = 21.

Soient B et B’ les cercles de centres I et J passant par A. Ces deux cercles se recoupent en B.
On appelle O l’intersection de (IJ) avec (AB) ainsi que C et D les symétriques de A par rapport à I et J.

1) Montrer que les points B, C et D sont alignés.

2) Montrer que la droite (CD) est parallèle à (IJ)

3) Dans le triangle AIJ, on pose : OI = x ; OJ = y et OA = h. Déterminer x, y et h.

4) Déterminer l’aire du triangle ACD.

Exercice 27 :

ABC est un triangle. La hauteur issue de B coupe (AC) en D et la hauteur issue de C coupe (AB) en E.

Dans le triangle ADE, la hauteur issue de D coupe (AB) en F et la hauteur issue de E coupe (AC) en H.
Montrer que les droites (FH) et (BC) sont parallèles.

3.2/5 - (11 votes)

Télécharger puis imprimer cette fiche en PDF.

Télécharger ou imprimer cette fiche «triangle : exercices de maths en 5ème corrigés en PDF.» au format PDF afin de pouvoir travailler en totale autonomie.

D'autres cours et exercices à consulter

Mathématiques Web c'est 2 268 325 fiches de cours et d'exercices téléchargées.