Priorités opératoires : exercices de maths en 5ème corrigés.

Mis à jour le 22 avril 2025

La priorités des opérations avec des exercices de maths en 5ème corrigés sur la priorités des opérations entre l’addition, la soustraction, la multiplication et la division.
L’élève devra maîtriser le vocabulaire concernant la somme, la différence, le produit et le quotient. En classe de cinquième, nous avons appris à travailler avec des nombres et à effectuer des opérations. Nous allons également étudié les priorités opératoires, qui sont des règles qui nous permettent de savoir dans quel ordre effectuer ces opérations pour obtenir le résultat correct. Vous devrez, également, savoir mener à bien des calculs plus complexes sur les priorités avec des parenthèses emboîtées.
Dans le plan, l’élève devra savoir placer un point connaissant ses coordonnées avec son abscisse et son ordonnée. Ces énoncés disposent de leur corrigé et peuvent être imprimer ou télécharger en PDF en cinquième.

Exercice 1

Calculer les expressions suivantes en écrivant les étapes intermédiaires :

a) 7 + 4 $\times$ 8 b) 3 $\times$ 11 − 7 $\times$ 4 c) 37 − 6 $\times$ 5 d) 9 − 4 : 4 e) 32 ÷ 4 − 2 + 7 $\times$ 3 f) 9 $\times$ 4 : 2 − 5 $\times$ 2

Exercice 2

Calculer les expressions suivantes en écrivant les étapes intermédiaires :

A = 6 $\times$ (3 + 7) B = 23 − 4 $\times$ 5 C = (3 + 5) $\times$ (9 − 7) D = (13 − 7) : 2 E = 5 − [4 − (2 + 1)] F = (3 + 5 $\times$ 7) : 2 +1

Exercice 3

Aurélie achète 5 pots de confitures à 1,50 € pièce et 12 baguettes à 0,95 € pièce.

Écrire un calcul te permettant de trouver le prix total qu’elle doit payer.

Exercice 4

Recopier sur ta feuille les expressions suivantes en ajoutant des parenthèses pour que l’égalité soit vraie :

8 + 2 $\times$ 5 = 50 ; 9 − 3 $\times$ 2 + 5 = 42 ; 8 + 4 $\times$ 3 : 2 = 18

Exercice 5

Calculer les expressions suivantes :

A = 24 − 5 − 1

B =14 $\times$ 3 − 5 $\times$ 2

C = 10 : [ 6 − 2 $\times$ (1 − 0,5) ] $\times$ 5

D = 8 : 4 − 0,25 $\times$ 2

E= 3 $\times$ (7 − 2) − 4

F = 72 : 9 $\times$ 8 : 2 − 9 $\times$ 3

Exercice 6

En utilisant autant de fois les nombres 3 ; 7 ; 10 et autant de fois que tu veux les signes + − $\times$ : ( ) essaie d’obtenir les résultats suivants :

20 ; 14 ; 31 ; 67 ; 40 ; 1.

Exercice 7

Mets les parenthèses et les crochets pour que l’égalité soit vraie :

5 $\times$ 4 − 1 + 2 $\times$ 2 = 34

Exercice 8

L’entraîneur d’une équipe de football doit acheter 16 équipements pour ses joueurs.

Chaque équipement est composé d’un maillot à 24€, d’un short à 11€ et d’une paire de chaussettes à 4,50€.

Écrire l’expression permettant de calculer le montant de ses achats.

Exercice 9

Un boxeur pèse 86,2 kg à une semaine d’un combat.

Il fait un régime qui lui permet de perdre 0,6 kg pendant 7 jours.

Écrire l’expression qui permet de calculer le poids du boxeur le jour du combat.

Exercice 10

Calculer les expressions suivantes:

A = 125 − 7 $\times$ 4 + 11

B = (125 − 7) $\times$ 4 + 11

C = 125 − 7 $\times$ (4 + 11)

D = 125 − (7 $\times$ 4) + 11

E = [(125 − 7) $\times$ 4] + 11

F = 125 − [7 $\times$ (4 + 11)]

Exercice 11 :

Calculer en respectant les priorités:

1) 12,7 + 3,1 $\times$ 2

2) 12,7 – 3,1 $\times$ 2

3) 12,7 $\times$ 3 + 3,1 $\times$ 7

4) 12,7 $\times$ 3 − 3,1 $\times$ 8

5) (5 − 3) $\times$ (9,1 − 7,8)

6) (5 + 3) $\times$ (9,1 + 7,8)

Exercice 12.

En écrivant les étapes intermédiaires, calculer les expressions suivantes :

A = − 4 + 15 + ( 9 – 4) – 2 + (−4 + 1 )

B = − 35 + [12 + ( 75 − 55) − (15 − 8 ) ] + 7

C = 4 − (7 – 3 ) − [ 11 − ( 8 − 5)]

Exercice 13.

Pour chaque égalité, indiquer si elle est exacte ou corriger en plaçant les parenthèses indispensables.

a) 6 + 5 $\times$ 5 – 3 = 28 b) 6 + 5 $\times$ 5 – 3 = 52

c) 6 + 5 $\times$ 5 – 3 = 16 d) 6 + 5 $\times$ 5 – 3 = 22

Exercice 14.

Calculer en indiquant les étapes intermédiaires :

A = 25 − 7 $\times$ (8 − 5) B = (7 − 4) $\times$ 3 + 4 − (7 $\times$ 2 − 8)

C = 8 $\times$ 3 − (12 : 3 + 2) $\times$ 3 D = [10 + 5 $\times$ (6 – 4)] : 4

Exercice 15

Relier par une flèche chaque calcul à son résultat :

(5 + 5) $\times$ (5 + 5) · · 6

5 $\times$ (5 + 5 + 5) ) · · 10

5 + ((5 + 5) $\times$ 5) · · 55

(5 + 5) $\times$ (5 : 5) · · 75

(5 + (5 $\times$ 5)) : 5 · · 100

Exercice 16.

Au rayon lait d’un supermarché, il y a au début de la journée 52 packs de 6 bouteilles de lait chacun.

Dans la journée, il s’est vendu 18 packs entiers et 63 bouteilles à l’unité.

1) Écrire une expression avec parenthèses permettant de calculer le nombre de bouteilles restant dans le rayon à la fin de la journée.

2) Écrire aussi une expression sans parenthèse.

3) Faire le calcul.

Exercice 17.

On donne l’expression littérale E = 2x + y (3y − x ) − 5

1) Calculer E lorsque x = 2 et y = 3

2) Calculer E lorsque x = 3,5 et y = 1

3) Calculer E lorsque x = 3 et y = 2

Exercice n° 18 :

Effectuer les calculs suivant en soulignant le calcul en cours.

A=24+3×7 B=720 : 9+4

C=60-14+5×3+2 D=8×3-5×4×0,2

E=15 :5-2

Exercice n°19 :

Effectuer les calculs suivant en soulignant le calcul en cours.

A=25-(8-3)+1 B=25-(8-3+1)

C=18-[4×(5-3)+2] D=[2+0,1×(5+3)] :4 E=24 :[8-(3+1))]

Exercice n° 20 :

Placer les parenthèses pour que les égalités suivantes soient vraies et vérifier chacune de vos réponses.

a) 4×2+9=44 b) 1+13-14-7=7 c) 15-3×2=24

d) 2×5-2×4+1=30 e) 32 – 4+7×2=10 f) 7+7+6×7=98

Exercice n° 21 :

Associer chaque expression à une phrase :

7×(4+3) · · La différence du produit de 4 par 3 et de 7

7×4+3 · · Le produit de 7 par la somme de 4 et de 3

4×3-7 · · Le produit de la différence de 7 et 4 par 3

(7-4) ×3 · · La somme du produit de 7 par 4 et de 3

Exercice n° 22 :

Traduis chaque phrase par une expression mathématique .

a) A est la somme du produit de 5 par 2 et de 3 alors A=……

b) B est le produit de 4 par la somme de 9 et de 7 alors B=…..

c) C est la différence de 17 et du produit de 4 par 3 alors C=…..

d) D est le quotient de la somme de 19 et 3 par 11 alors D=….

Exercice n° 23 : parenthèses emboitées.

Calculer les expressions suivantes sur votre cahier.

A=35-[4× (5+2)-7]

B=12×[32-(4+7) ×2]

C=(1+7) ×[11-(2+3)]

D=12+[(120-20)-2×4×5]

E=150-10-[(12+2) ×4+2]

F=(60-59,9) ×[30-(25-15)]

Exercice 24 :

I) Calculer :

$A = 12 + 8 \times 5 - 4 + 16 : 2$

$B = 17 - (3 + 8 -5)$

$C = 18 + 4 \times (7 \times 2 - 6)$

$D = 75 - (6 + 3 \times 10) : 9$

$E = 3 200 \times 0,01 \times 100-100$

$F = (5,6 + 1,4) \times (3,4- 1,4)$

$G = 48 + 2 \times (7 + 3 \times 5 - 2 \times 10)$

$H = 5 + 3 \times 6 - 8 : 2$

$I = 24,1 -[9 - (2 + 5)]$

$J = 15,1 - [17- (30 - 20)]$

$K = 128 - 4 \times (6 + 1) + 218 - 3 \times (7 - 1)$

$L = 8 + 2 \times (15 - 5 \times 2 + 4)$

$M = 8 \times [9 - (2 + 4)] - 5 + 2$

$N = 6 + 4 \times [2 \times (11 - 4 \times 2 + 2) - (9 - 5)]$

O = 17 − [3 × (5 − 2) + 8] + 12,3 × 4 − 4

$P = 3,5 \times [12 - (7 + 3)]$

Q = 2,5 × [3 + 2 × (13 − 3 × 3) − 6 − 3]

R = 38 − 8 × (7 − 2 × 3 + 1) − 4 + 2

S = 6 + 2 × 8 – 5 × 3 + 10 : 2

T = [(6 + 2) × (8 – 5) × 3 + 10] : 2

U = 6 + [2 × (8 – 5) × 3 + 10 : 2]

V = (19 – 7) × 4 – (28 – 14)

W = 25 – [18,7 – (9,2 + 4,5)]

X = [35 – (17 – 6)] : 8

Y = 2 × [(25 – 17,1) × 3 + 11,3]

Z = [35 – 56 : (28 – 20)] × 10

II) Calculer astucieusement :

$A = 123,45 + 89,12 + 546,55 + 15,15 + 40,88$

$B = 8 \times 8765,43 \times 4 \times 0,125 \times 2,5$

$C = 45,13 + 136,38 + 124,87 + 56,48 + 72,62$

$D = 0,4 \times 56,49 \times 12,5 \times 25 \times 0,08$

$E = 56,98 + 76,59 + 34,18 + 14,02 + 12,41$

$F = 17,3 + 12 \times 2 + 1,4 + 2,7 + 2,3 \times 2$

$G = 2 - 1,2 + 0,71 + 1,1 \times 2 + 12 + 0,29$

$H = 0,123 + 0,1 + (0,577 + 0,2)$

Exercice 25 :

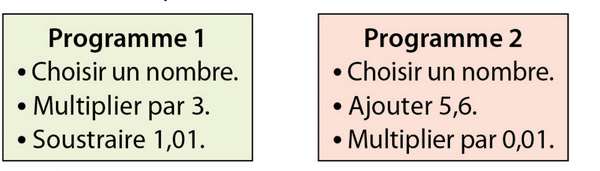
a. Pour chacun des programmes de calcul ci-dessous, écrire une expression qui permet de
calculer le nombre obtenu lorsqu’on choisit 0,7 comme nombre de départ.

b. Calculer ces expressions.

Exercice 26 :

a. Laquelle de ces expressions correspond à la description de Sofiane ?
$C=(5,29 \times 10+78) \times 001 \,\,D=5,29 \times (10+ 78) \times 0,01 \\E=5,29 \times 10+78 \times 0,01\,\, F=5,29 \times (10+78 \times 0,01)$
b. Calculer cette expression.

Exercice 27 :

Associer l’une des expressions À, B, C ou D à chacun des trois problèmes, puis donner les
réponses aux problèmes.
$A=5 \times (4+8) \,\,B=4+5 \times 8 \\C=5+4 \times 8 \,\, D=5 \times 4+5 \times 8$

Exercice 28 :

Calculer à la main chaque expression.
$A=21,4-(24-7):2 \\B=(13-4) \times 0,6-3,8 \\C= 34,5 - 30 \times (1 - 0,6) \\D=(16+2):5-2$

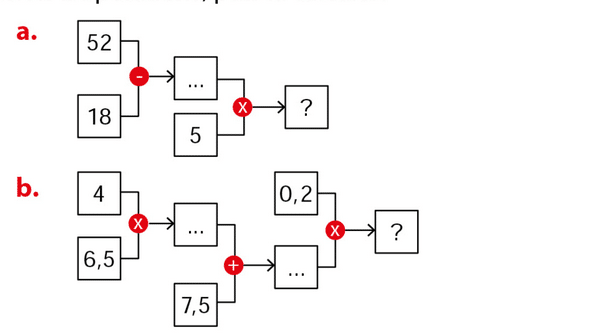
Exercice 29 :

Écrire l’expression qui correspond à la succession d’opérations, puis la calculer.

Exercice 30 :

Voici les achats que Clara veut effectuer avec un billet de 50€.

1. Expliquer à l’aide d’ordres de grandeur pourquoi le billet de 50 € suffira.
2. a. Écrire l’expression R qui permet de calculer la somme que l’on rendra à Clara.
b. Calculer R.

Télécharger puis imprimer cette fiche en PDF.

Télécharger ou imprimer cette fiche «priorités opératoires : exercices de maths en 5ème corrigés en PDF.» au format PDF afin de pouvoir travailler en totale autonomie.

Nos applications

Mathématiques Web c'est 2 268 971 fiches de cours et d'exercices téléchargées.

Continuez votre apprentissage

Cours de cinquième

Exercices de cinquième