Probabilités : exercices de maths en terminale corrigés en PDF.

Les probabilités à travers des exercices de maths en terminale corrigés qui vous donneront la possibilité de réviser en ligne. Cette fiche est à consulter ou en téléchargement gratuit au format pdf.

Vous retrouverez tous les savoirs-faire exigibles dans les programmes officiels de l’éducation nationale.

Les probabilités sont un outil important pour comprendre et modéliser des phénomènes aléatoires. En classe de terminale, les élèves étudient en détail les probabilités et leur utilisation et ses propriétés à travers des expériences aléatoires dans divers contextes. Ces énoncés disposent de leur correction afin de combler vos lacunes sur les probabilités et de vous permettre de vous exercer dans l’objectif d’augmenter vos notes en terminale.

Exercice n° 1 :

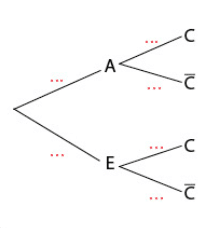
Une école organise en cours d’année un test de langues vivantes.

Tous les étudiants doivent étudier l’anglais et l’espagnol.

Le jour de l’épreuve, un étudiant tire un sujet au hasard parmi les sujets préparés.

La probabilité pour que ce soit un sujet d’anglais (A) est de 0,8.

Si c’est un sujet d’anglais, la probabilité que ce soit un texte qu’il connait (C) est de 0,3 et si c’est un sujet d’espagnol (E), la probabilité que ce soit un texte inconnu est de 0,2.

1.Reproduire et compléter l’arbre des probabilités ci-dessous.

2.a.Lire sur l’arbre les valeurs de P(E) et .

b. En déduire la valeur de $P(E\,\cap\, C)$ et interpréter le résultat obtenu.

Exercice n° 2 :

Un jeu est constitué d’un tiers de questions sur le cinéma et de deux tiers de questions sur la musique. On pose à Robin une question tirée au hasard dans ce jeu.

On sait qu’il a une chance sur deux de répondre correctement à la question posée si elle porte sur le cinéma et trois chances sur quatre si elle porte sur la musique.

a) Représenter cette situation par un arbre de probabilités.

b) Calculer la probabilité de l’événement « la question porte sur la musique et Robin ne répond pas correctement ».

Exercice n° 3 :

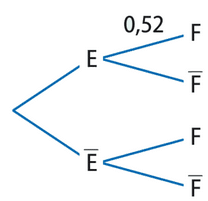
On considère deux événements E et F associés à une expérience aléatoire.
1. On sait que P(E) = 0,65, = 0,52 et $P_{\overline{E}}(F) = 0,36$ .

Recopier et compléter l’arbre pondéré ci-dessous.

2. Préciser les valeurs de $P(\overline{E})$ , $P_{ E }(\overline{F})$ et $P_{ \overline{E} }(\overline{F})$ .

3. Expliquer pourquoi $P(E \cap F)$ = 0,338.

4. Calculer $P(E \cap \overline{F})$ , $P(\overline{E }\cap F)$ et $P(\overline{E} \cap \overline{F})$ .
Exercice n° 4 :

A et B désignent deux événements de l’ensemble des issues d’une expérience aléatoire.

Sachant que A et B sont indépendants, déterminer P (B) dans chacun des cas
suivants.

1. P(A)=0,56 et P(A $\cap$ B)=0,21.

2.P(A)= $\frac{1}{3}$ et P(A $\cap$ B)= $\frac{3}{25}$ .
Exercice n° 5 :

Dans une population, 84 % des personnes possèdent un téléphone portable et 75 % des personnes possèdent un ordinateur. De plus, 60 % des personnes de cette population déclarent posséder à la fois un téléphone portable et un ordinateur.

On interroge au hasard une personne de cette population.
On considère les événements :

– T:« la personne interrogée possède un téléphone
portable » ;

— O : «la personne interrogée possède un ordinateur ».

1. Donner les valeurs de P(T), P (O) et P(T $\cap$ O); puis déterminer $P (\overline{T})$ et $P(\overline{O})$ .

2. Construire un tableau de probabilités correspondant à cette situation.

3. Calculer la valeur de $P_T(\overline{O})$ .

4. Sachant que la personne interrogée a un ordinateur, déterminer la probabilité qu’elle possède aussi un téléphone portable.

Exercice n° 6 :

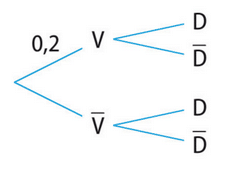
Dans un cybercafé, la probabilité qu’un ordinateur soit infecté par un virus durant la journée est 0,2.
Si un virus est présent, le logiciel antivirus indique sa présence dans 96 % des cas.

S’il n’y pas de virus, le logiciel antivirus indique néanmoins la présence d’un virus dans 5 %

des cas.
On choisit au hasard un ordinateur du cybercafé et on note V l’événement « l’ordinateur est infecté par un virus » et D l’événement « le logiciel antivirus a détecté un virus ».

1. Préciser les valeurs de P(V), et $P_{\overline{V}}(D)$ .

2. Reproduire et compléter l’arbre pondéré ci-dessous.
3. Déterminer P(V $\cap$ D) et interpréter cette probabilité.

Exercice n° 7 :

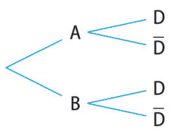
Une usine de composants électriques dispose de deux unités de production, A et B.

La production journalière de l’usine A est de 600 pièces, celle de l’unité B est de 900 pièces.
On prélève au hasard un composant de la production d’une journée.

La probabilité qu’un composant présente un défaut de soudure sachant qu’il est produit par l’unité A est 0,014.

La probabilité qu’un composant présente un défaut de soudure sachant qu’il est produit par l’unité B est égale à 0,024.
On note: D l’événement «le composant présente un défaut de soudure »,

A l’événement «le composant est produit par l’unité A»

et B l’événement «le composant est produit par l’unité B ».
1. Préciser les valeurs de P(A), P(B), et .

2. Recopier et compléter l’arbre de probabilités ci-dessous.

3. a. Calculer P(A $\cap$ $\overline{D}$ ) et P(B $\cap$ $\overline{D}$ ), puis interpréter ces probabilités.
b. En déduire P (D).
4. On prélève dans la production totale un composant présentant un défaut de soudure.
Quelle est la probabilité qu’il provienne de l’unité A ?

Exercice n° 8 :

Agathe, qui vient d’apprendre qu’elle a réussi son examen du code de la route, appelle chacun
de ses parents sur leurs téléphones portables pour leur annoncer la nouvelle.

On note A l’événement « son père répond à son appel » et B l’événement « sa mère répond à
son appel ».

On sait que P (A) = 0,8 et P (B) =0,75.

De plus, on fait l’hypothèse que ces deux événements sont indépendants.

1. Quelle est la probabilité qu’Agathe puisse annoncer la nouvelle à ses deux parents ?

2. Calculer $P (\overline{A} \cap \overline{B})$ . À quel événement correspond cette probabilité ?

Exercice n° 9 :

A et B sont deux événements.

On a P(A) = $\frac{1}{4}$ , $P(A \cup B)= \frac{1}{3}$ et .

1. Calculer dans chacun des cas suivants :
a. A et B sont incompatibles ;

b. A et B sont indépendants ;

c. A est une partie de B.

2. Dans chacun de ces cas, calculer et .

Exercice n° 10 :

L’efficacité du vaccin contre la grippe peut diminuer en fonction des caractéristiques des personnes
vaccinées, ou en raison du vaccin, qui n’est pas toujours totalement adapté aux souches du virus qui circulent.
II est donc possible de contracter la grippe en étant vacciné.
Une étude menée à l’issue de la période hivernale a montré que :
• 40 % de la population est vaccinée
• 8 % des personnes vaccinées et 28 % des personnes non vaccinées ont contracté la grippe.
On choisit une personne au hasard dans la population.
V est l’événement : « La personne est vaccinée » ;
G est l’événement : « La personne a contracté la grippe ».
a) Représenter la situation par un arbre pondéré.
b) Déterminer la probabilité que la personne choisie ait contracté la grippe.
c) La personne choisie a contracté la grippe.
Déterminer la probabilité qu’elle soit vaccinée.
d) Déterminer la probabilité que la personne choisie ait contracté la grippe ou soit vaccinée.

Exercice n° 11 :

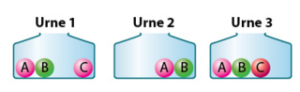
On prélève au hasard une boule de chacune des urnes ci-dessous.

Situation 1 : on note la couleur des boules tirées.
V est l’événement « La boule tirée est verte ».
a) Reproduire et compléter l’arbre ci-dessous.

b) Déterminer la probabilité de tirer au moins une boule verte.
Situation 2 : on note la lettre indiquée sur chaque boule tirée.
A est l’événement : « La boule tirée porte la lettre A ».
a) Représenter la situation par un arbre pondéré.
b) Déterminer la probabilité d’obtenir A une fois au plus.

Exercice n° 12 :

Une roseraie livre des fleuristes par lots de 100 roses.
Afin de fidéliser ses clients, elle rembourse un lot lorsqu’il contient strictement plus de 5 roses fanées.
Une étude a montré que 4 % des roses livrées sont fanées.
On choisit un lot au hasard.
X est la variable aléatoire qui donne le nombre de roses fanées de ce lot.
1. a) Quelle est Ia loi de probabilité suivie par X ?
b) Calculer la probabilité que le lot soit remboursé au fleuriste.

Arrondir au centième.
2. Le chef des ventes de la roseraie souhaite réduire le nombre de lots remboursés.

Pour cela, il décide d’augmenter le nombre k de roses fanées partir duquel le
lot est remboursé.
a) Écrire une fonction Seuil en langage Python qui détermine la plus petite valeur k

telle que la probabilité de rembourser le lot soit inférieure ou égale à 0,01 .
b) Saisir et exécuter cet algorithme.

Exercice n° 13 :

Au casino, le jeu de la roulette contient 37 numéros (de 0 à 36).
On a détaillé ci-dessous cinq façons de jouer une partie à la roulette.

(1) Miser sur l’un des 37 numéros.
(2) Miser sur « Impair ».
(3) Miser sur« l à 18».
(4) Miser sur « Rouge».
(5) Miser sur « 1 er 12 », c’est-à-dire sur les 12 premiers numéros de 1 à 12.
Un joueur décide de jouer quatre parties successives en misant, à chaque fois, de la même façon.
X est la variable aléatoire qui compte le nombre de parties gagnées sur les quatre parties jouées.
Pour chaque façon de miser :
a) modéliser la situation par une loi binomiale dont on précisera les paramètres ;
b) déterminer la probabilité que le joueur gagne au moins une partie. Arrondir au millième.

Exercice n° 14 :

Un serveur a étudié les pourboires laissés par ses clients durant l’année écoulée.
II a constaté que 25 % des clients ne laissent pas de pourboire et que les autres laissent un pourboire moyen de 1,80 €.
On prélève au hasard un échantillon de 50 clients de ce restaurant.

On suppose que les paiements des clients sont indépendants.
X est la variable aléatoire qui compte le nombre de clients ayant laissé un pourboire.
Les résultats seront arrondis au millième.
a) Déterminer et interpréter P(X = 35).
b) Déterminer la probabilité de l’événement :

« Avec ces 50 clients, le restaurateur a reçu 72 € de pourboires ».

c) Déterminer $P(35\leq\, X \leq\, 40).$
Interpréter le résultat obtenu.

4.7/5 - (11 votes)

Télécharger puis imprimer cette fiche en PDF.

Télécharger ou imprimer cette fiche «probabilités : exercices de maths en terminale corrigés en PDF.» au format PDF afin de pouvoir travailler en totale autonomie.

D'autres cours et exercices à consulter

Mathématiques Web c'est 2 267 942 fiches de cours et d'exercices téléchargées.

Télécharger puis imprimer cette fiche en PDF.

D'autres cours et exercices à consulter

Cours de terminale

Exercices de terminale

Nos applications