Symétrie centrale : cours de maths en 5ème en PDF.
La symétrie centrale avec un cours de maths en 5ème nécessaire pour la progression de l’élève.
Cette leçon fait intervenir les notions suivantes :
– La définition
– propriété de conservation des longueurs;
– propriété de conservation des mesures d’angles;
– conservation de l’alignement;
– conservation du parallélisme;
– transformation d’une droite en une autre droite parallèle;
– conservation du périmètre d’une figure;
– conservation de l’aire d’une figure géométrique.
L’élève devra savoir construire l(image d’une figure par une symétrie centrale de centre O mais également, utiliser les différentes propriétés de conservation pour effectuer des démonstrations en géométrie pour le niveau cinquième et tout au long de sa scolarité.
I. Définition de la symétrie centrale
1.Symétrie centrale et demi-tour
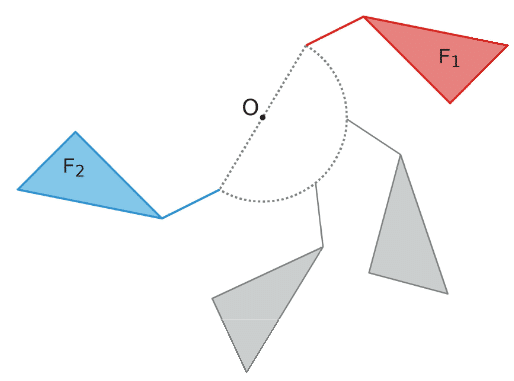
Deux figures et
sont symétriques par rapport à un point O lorsque l’onpeut passer de l’une à l’autre par un demi-tour de centre O, soit une rotation d’un angle de 180° et de centre O.
La figure est appelée l’image de
par la symétrie centrale de centre O.
Exemple :
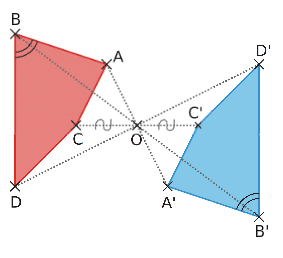
- La figure
est le symétrique de la figure
par rapport au point O.
- De même, la figure
est le symétrique de la figure
par rapport au point O.
- Les figures
et
sont symétriques par rapport au point O.
- On dit également que le point O est le centre de la symétrie qui transforme la figure
en la figure
.
2.Symétrique d’un point
On considère une symétrie centrale de centre O.
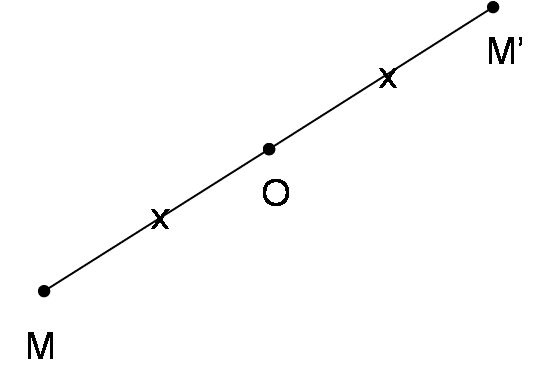
Le point M’ est l’image du point M par la symétrie centrale de centre O
si et seulement si le point O est le milieu du segment [MM’].
Exemple :
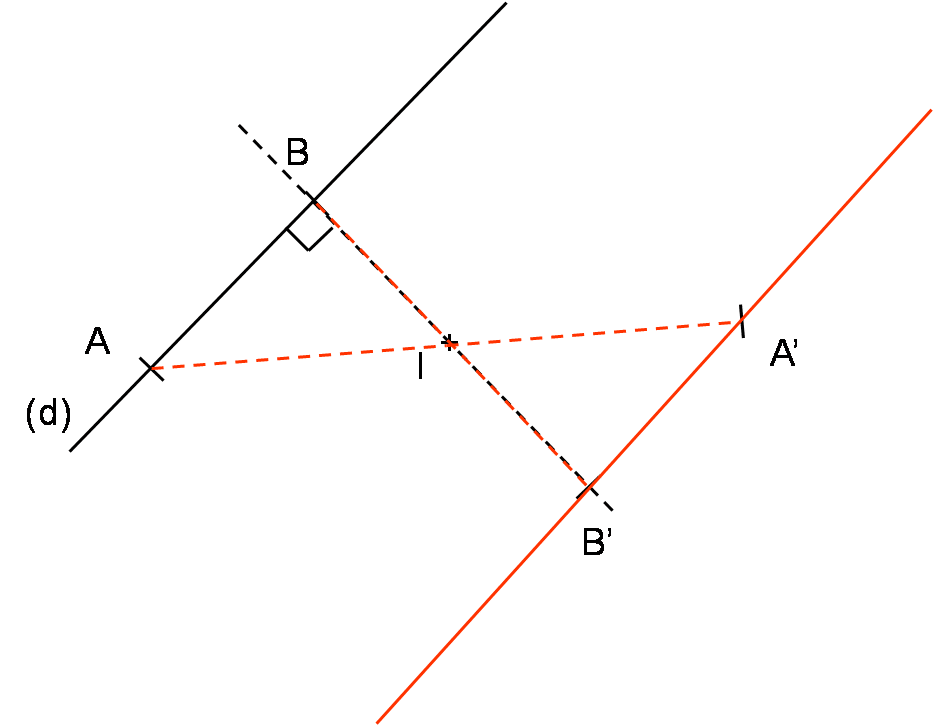
- Le symétrique de A par rapport à O est A’.
- Le symétrique de A’ par rapport à O est A.
- A et A’ sont symétriques par rapport à O.
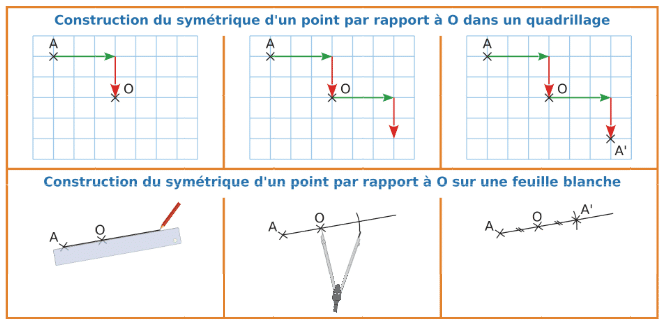
Remarque :
II.Les propriétés de la symétrie centrale
1.symétrique d’un segment
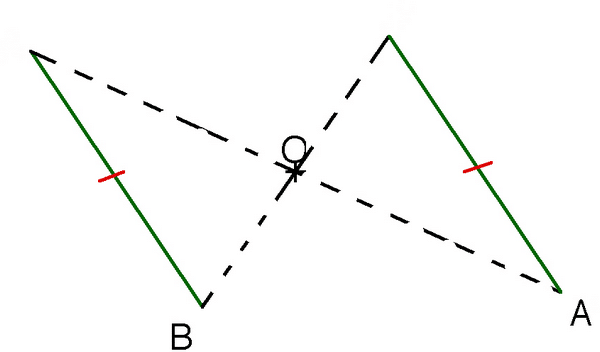
- Le symétrique d’un segment par une symétrie centrale est un segment de même longueur.
- La symétrie centrale conserve les longueurs de segments, les périmètres et les aires de figures géométriques.
- Pour construire le symétrique du segment [CD] par rapport au point O, on construit le symétrique des points C et D, noté C’ et D’, par rapport au point O.
- Par la symétrie de centre O, le symétrique du segment [CD] est alors le segment [C’D’] .
- Le symétrique du milieu d’un segment est le milieu du segment symétrique.
2.Symétrie d’une droite
- L’image d’une droite par une symétrie centrale est une droite qui lui est parallèle.
- La symétrie centrale transforme une droite en une autre droite qui lui est parallèle.
3.Symétrique d’un polygone
La symétrie centrale conserve tout, principalement :
- les longueurs;
- les périmètres de figures;
- les aires de figures;
- les mesures d’angles;
- le parallélisme;
- l’orthogonalité.
Le symétrique d’un polygone est un polygone possédant le même nombre de côtés et ayant la même forme.
Pour construire le symétrique d’un polygone, on construit le symétrique de chaque côté puis,
on relie les sommets dans le bon ordre.
4.Symétrique d’un cercle
Le symétrique d’un cercle est un cercle de même rayon et ayant pour centre le symétrique du centre du premier cercle.
Remarque :
Pour construire le symétrique d’un arc de cercle par rapport à un point, on construit les symétriques du centre et des extrémités de l’arc de cercle symétrique.
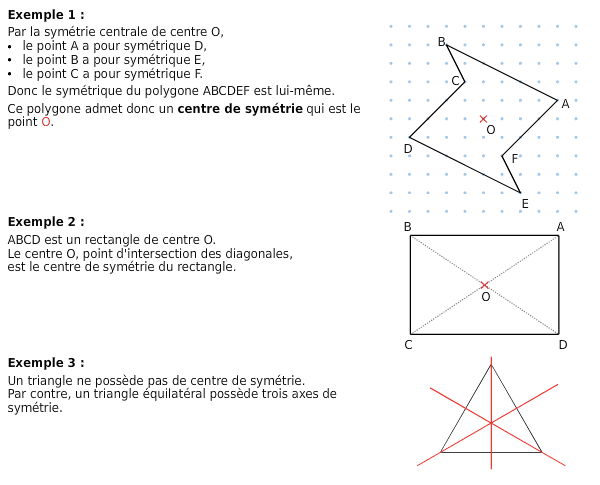
III.Centre de symétrie d’une figure
Un point O est le centre de symétrie d’une figure si l’image
de la figure est confondue avec
.
Télécharger ou imprimer cette fiche «symétrie centrale : cours de maths en 5ème en PDF.» au format PDF afin de pouvoir travailler en totale autonomie.
D'autres cours et exercices à consulter
- Propriétés de géométrie : cours de maths en 5ème en PDF.
- Triangles : cours de maths en 5ème en PDF.
- Calcul littéral : cours de maths en 5ème en PDF.
- Nombres relatifs : cours de maths en 5ème en PDF.
- Volumes : cours de maths en 5ème en PDF.
- Probabilités : cours de maths en 5ème en PDF.
- Angles : cours de maths en 5ème en PDF.
- Statistiques : cours de maths en 5ème en PDF.