Intervalles : exercices de maths corrigés 2de à télécharger en PDF.

Les intervalles et les ensembles de nombres à travers des exercices de maths en 2de. Pour bien comprendre ce chapitre, il faut faire régulièrement s’exercer car c’est une notion assez particulière et technique. Vous vou exercerez sur des unions et des intersections d’intervalles et leur écriture à l’aide d’une valeur absolue seconde.

Exercice 1 :

Recopier et compléter le tableau ci-dessous :

Enoncé	Intervalle	Représentation graphique
$-1\leq\, x<3$	x $\in$
	x $\in$
$-7\geq\, x> -8$	x $\in$
$x\in \mathbb{R}^+$	x $\in$
$x\neq 5$	x $\in$

Exercice 2 :

Traduire sous forme d’intervalle :

1) y > – 3 et y < 4 2) y > – 3 ou y < 4

3) $y\leq\, \frac{1}{3}$ et $y\leq\, \frac{1}{2}$ 4) $y\leq\, \frac{1}{3}$ ou $y\leq\, \frac{1}{2}$

Exercice 3 :

Compléter avec les symboles $\in$ ou $\notin$ :

1) 7 … ] 0 ; 7 [

2) 5,9 … ] 5,8 ; +∞ [

3) – 0,25 … ] – 0,3 ; – 0,2 [ … ] 1 ; 2 ]

4) – 0,199 … ] – 0,2 ; – 0,19 [

5) $\pi$ …. [ 3,14 ; 3,141 [

Exercice 4 :

Vrai ou faux ?

1) Si x ∈ [ 6,7 ; +∞ [ alors x ∈ [ 6 ; +∞ [.

2) Si x ∈ ] – 3 ; 4 [ alors x ∈ [ – 2 ; 5 [.

3) Si x ∉ [ – 5 ; 2[ alors x ∈ ] $-\infty$ ; – 3 [ ∪ [ 2 ; +∞[.

4) L’intervalle ] 0 ; 4[ est inclus dans [ 0 ; 4 [.

5) $\mathbb{N} \subset \mathbb{Q}^+$ .

6) Si $x \notin \mathbb{Q}$ alors $x \notin D$ .

Exercice 5 :

Simplifier les notations suivantes lorsque c’est possible.
A = [ – 5 ; 7[ ∪ [ – 2 ; 12 [
B = [ 0 ; +∞ [ ∪ ] – 2 ; +∞ [
C = ] –∞ ; 0 [ ∪ [ 0 ; +∞ [
D = ] -∞ ; 4/3 [ ∩ [ – 10 ; 10 ]
E = [ – 4 ; [ ∪ ] $\frac{1}{2}$ ; 10]

Exercice 6 :

Représenter I et J sur une droite graduée, puis déterminer I ∩ J et I ∪ J.

1) I = [ 2 ; 5,5 ] et J = ] 1 ; 3 ].

2) I = [ – 1 ; +∞ [ et J = ] –2 ; 3 ].

3) I = ] – 1 ; 3 ] et J = [ – $\sqrt{2}$ ; $\pi$ [.

4) $I = \mathbb{R}^-$ et $J = \mathbb{R}^+$ .

5) I = {1 ; 2 ; 3 ; 4} et J = [ – 5 ; 5 ].

Exercice 7 :

On considère des droites graduées sur lesquelles on a marqué des ensembles de nombres.

Donner l’intervalle correspondant.

Exercice 8 :

Représenter sur une droite graduée et décrire, à l’aide d’un intervalle, chacun des ensembles de nombres réels tels que :

a) $0\leq\, x\leq\, 3$ b)

c) $x\leq\, 9$ d)

Exercice 9 :

Représenter sur une droite graduée chacun des intervalles suivants.

a) b)

c) $]-\infty;2]$ d) $[0;+\infty[$

Exercice 10 :

Ecrire les inégalités vérifiées par les réels pour chacun des cas suivants.

a) $x\in[0;1,2]$ b) $x\in]-\frac{5}{3};3]$

c) $x\in[4,73;+\infty[$ d) $x\in ]-\infty;0[$

Exercice 11 :

Recopier et compléter par les signes $\in$ et $\notin$ .

a) b) $-\pi...]-3;-1[$

c) $6...[\frac{7}{3};+\infty[$ d) $-3... ]-\infty;-3,5[$

Exercice 12 :

Sans calculatrice, dire si $\frac{2}{3}$ appartient aux intervalles suivants.

a) $[0;\frac{4}{5}]$ b) $[\frac{3}{5};1]$ c) $[\frac{1}{3};\frac{2}{5}]$

Exercice 13 :

Soit et .

Dire si chacun des nombres suivants appartient à I, à J, à $I\cap J$ , à $I\cup J$ .

a) – 10 b) – 6 c) – 0,5 d) 2

e) 8,1 f) 99,9 g) 1 000 h) 0

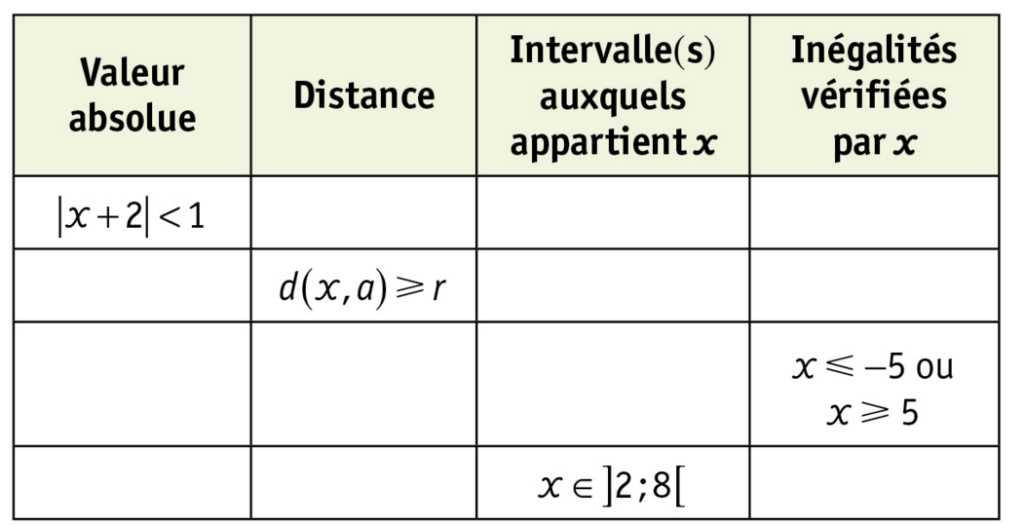
Exercice 14 :

Compléter le tableau suivant :

Exercice 15 :

Parmi les affirmations suivantes, lesquelles sont vraies ?
Justifier.
a. Quels que soient les réels a et b, .
b. Si alors x=0.
c.
d. .

4.1/5 - (11 votes)

Télécharger puis imprimer cette fiche en PDF.

Télécharger ou imprimer cette fiche «intervalles et ensembles de nombres : exercices de maths en 2de corrigés en PDF.» au format PDF afin de pouvoir travailler en totale autonomie.

D'autres cours et exercices à consulter

Mathématiques Web c'est 2 268 522 fiches de cours et d'exercices téléchargées.