Théorème de Pythagore : exercices de maths en 4ème corrigés.

Le théorème de Pythagore avec des exercices de maths en 4ème corrigés vous aidera à développer des connaissances intéressantes. L’élève devra savoir appliquer la partie directe afin de calculer la longueur d’un triangle rectangle puis, la partie réciproque afin de vérifier si un triangle possède un angle droit. De plus vous pourrez développer vos compétences avec à travers divers problèmes corrigés similaires à ceux de votre manuel scolaire.

Exercice 1 :

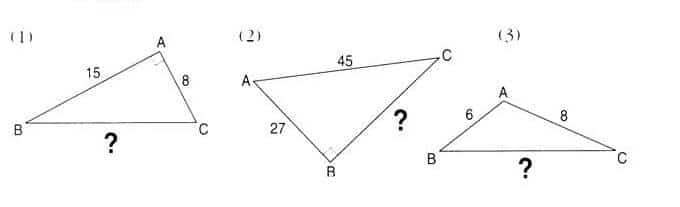
1) Dans chacun des cas suivants, calculer, si possible, la longueur BC.

Toutes les longueurs sont données en centimètres.

2) RST est un triangle rectangle en R tel que RS = 2 cm et RT = 1 cm. Calculer ST.

Le résultat en centimètres est-il un nombre entier ? Sinon, trouver un arrondi de ST au dixième de centimètre près.

Exercice 2 :

Qui a raison ?

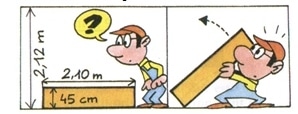
Exercice 3 : La surprise finale

Le plafond est-il assez haut pour que Monsieur Bricoltou mette en place son meuble ?

Exercice 4 :

Une chèvre C est attachée à un piquet P planté au coin d’un pré carré de 15 m de côté.

Quelle doit être, approximativement, la longueur de la corde pour que la chèvre puisse brouter tout le pré?

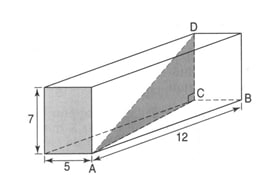
Exercice 5 : Le parallélépipède rectangle

Combien mesure à 0,01 près, la diagonale du parallélépipède rectangle?

Exercice 6 :

Monsieur Crésus possède un terrain VAGUE qu’il veut clôturer.

Calculer le périmètre du terrain VAGUE.

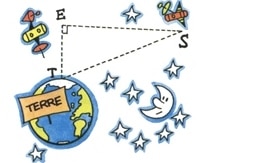
Exercice 7 :

Quelle distance sépare les deux satellites E et S, sachant que l’angle $\widehat{TES}$ est droit et qu’un signal radio met $\frac{1}{60}$ de seconde de S à T et $\frac{1}{100}$ de seconde de E à T ?

(Vitesse du signal radio : 300 000 km/s.)

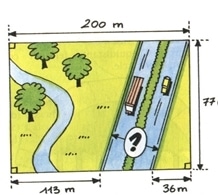
Exercice 8 :

Quelle est la largeur de l’autoroute ?

(Non, ce n’est pas 51 mètres !)

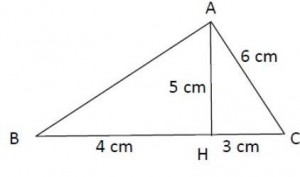
Exercice 9 : la hauteur d’un triangle

La droite (AH) est-elle une hauteur du triangle ABC ?

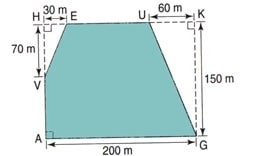
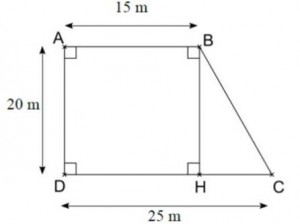
Exercice 10 : la clôture d’un jardin

Monsieur Maud achète 80 mètres de grillage pour clôturer son jardin dont la forme et les dimensions sont données par la figure ci-dessous :

Aura-t-il assez de grillage ?

Justifier la réponse.

Clôture d'un jardin — Clôture d’un jardin

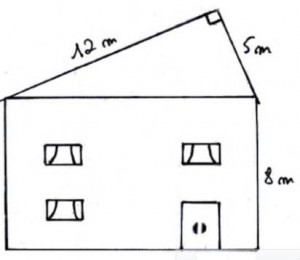
Exercice 11 :la façade d’une grande case de St-Pierre

La figure ci-contre représente la façade d’une grande case de St-Pierre.

Les trois fenêtres ont la même dimension (2.00 m x 1.00m)

La porte mesure 2.00 m x 2.40 m

Une entreprise se charge de peindre cette façade.

Un bidon de peinture de 10 L coûte 75 € et permet de couvrir une surface de 50 m².

On souhaite passer 2 couches de peinture sur la façade de cette case. Calculer le nombre de bidons nécessaires ainsi que le coût de la peinture.

Dans cet exercice, toute trace de recherche, même non aboutie, sera prise en compte dans l’évaluation.

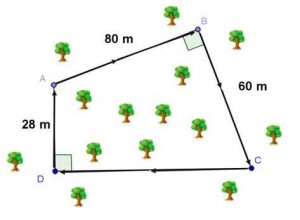
Exercice 12 : le parcours d’endurance du CROSS du collège

Voici une représentation du parcours d’endurance des élèves d’une classe de 4°.

Ils doivent parcourir une distance de 1,4 km en partant du point A et en suivant le sens des flèches.

Où doivent-ils arriver ?

Parcours d'endurance — Parcours d’endurance

Exercice 13 :

La voile MAT de ce bateau peut être assimilée un triangle rectangle en A, tel que :
AM = 3,81 m et TM = 9,76 m.

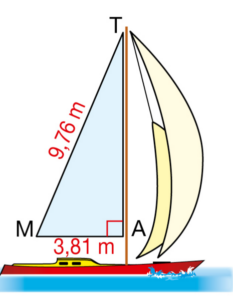
Calculer une valeur approchée au centième prés de la longueur AT, en m.

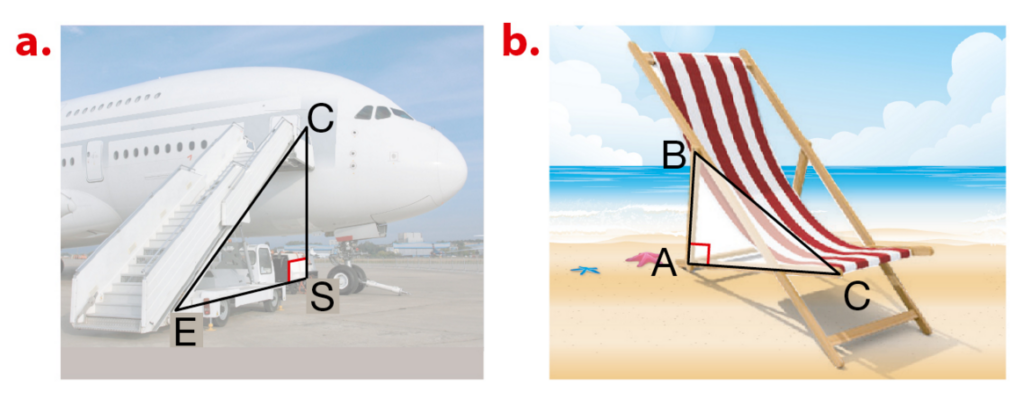
Exercice 14 :

Pour le triangle rectangle repéré sur chaque photo, appliquer le théorème de Pythagore.

Exercice 15 :

Le cadre de ce BMX est un triangle ABC rectangle en B avec :
AB = 50 cm et BC = 20 cm.

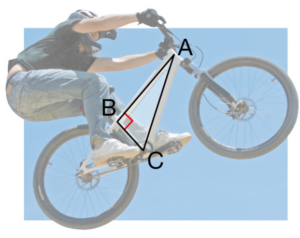
Calculer la longueur du tube inférieur [AC], en cm.

Donner une valeur approchée au dixième près de cette longueur.

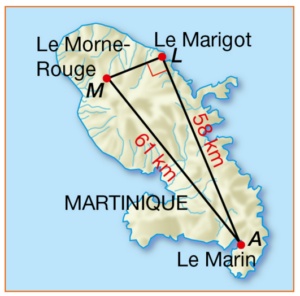
Exercice 16 :

Sur cette carte de Martinique, le triangle MLA (où M désigne Le Morne-Rouge, L Le Marigot et A Le Marin) est rectangle en L.
Utiliser les informations codées, pour calculer la distance LM à vol d’oiseau, en km.

Donner une valeur approchée au dixième près de cette distance.

4.2/5 - (17 votes)

Télécharger puis imprimer cette fiche en PDF.

Télécharger ou imprimer cette fiche «théorème de Pythagore : exercices de maths en 4ème corrigés en PDF.» au format PDF afin de pouvoir travailler en totale autonomie.

D'autres cours et exercices à consulter

Mathématiques Web c'est 2 268 415 fiches de cours et d'exercices téléchargées.