Les statistiques avec un cours de maths en 2de. L’élève devra connaître les différentes définitions (population, caractère, étendue, mode) mais également, savoir calculer la moyenne et la médiane d’une série statistique.
I. Les statistiques : vocabulaire et définitions.
L’étude du vocabulaire et des notions de statistique du programme de 2de va être illustrée par un exemple.
La série statistique des notes de mathématiques obtenues par les élèves d’une classe de seconde lors de l’année scolaire précédente (en réalité, c’est la moyenne arrondie au demi-point supérieur des notes des 8 premiers devoirs surveillés de mathématiques réalisés dans cette classe).
On appelle population d’une série statistiques, l’ensemble auprès duquel l’enquête est menée.
Concrètement l’ensemble auprès duquel la question est posée.
On appelle individu un élément de la population.
Exemple:
Nous menons aune enquête auprès de 24 élèves d’une classe de seconde.
La population est les 24 élèves de cette classe de seconde et un individu est chaque élève composant cette classe de seconde.
Caractère étudié ou variable statistique:
Exemple:
Notes obtenues par les élèves de la classe de seconde pendant l’année scolaire précédente.
Les valeurs que peut prendre un caractère s’appellent les modalités.
De façon générale, un caractère peut être :
Quantitatif quand les valeurs sont numériques (mesures physiques, physiologiques, sociologique, démographiques, économiques, …)
Le caractère est dit discret lorsqu’il ne peut prendre qu’un nombre fini de valeurs numériques : c’est le cas de l’exemple étudié ici.
Le caractère est dit continu, lorsqu’il peut prendre une infinité de valeurs numériques : par exemple, la taille d’un élève est un caractère de type quantitatif continu.
Dans cette situation il est commode de regrouper les valeurs du caractère dans des classes : par exemple, on va regrouper les tailles des individus dans des classes d’amplitude 1 cm.
Qualitatif quand les valeurs ne peuvent être ni ordonnées ni ajoutées (groupe sanguin, couleur des yeux, vote pour un candidat).
Pour des raisons de facilité de traitement informatique ou mathématique, on cherche à se ramener à des caractères quantitatifs par un codage.
L’effectif d’une modalité est le nombre d’individus de la population possédant cette valeur du caractère.
Exemple:
L’effectif de la modalité « 10,5 » est :3. C’est le nombre d’élèves ayant la note 10,5.
L’effectif total est le nombre d’individus de la population.
C’est la somme des effectifs de chaque modalité.
Exemple:
L’effectif total est le nombre d’élèves de seconde pendant l’année précédente, c’est à dire : 35.
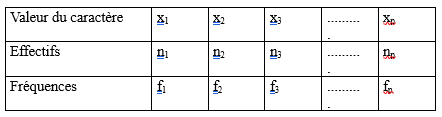
La série statistique des effectifs est la fonction qui, à chaque valeur du caractère (modalité), associe l’effectif de cette modalité.
Elle est le plus souvent définie à l’aide d’un tableau.
Exemple:
Voir tableau des données statistiques ci-dessous :
Comme pour les fonctions, les séries statistiques peuvent être représentées graphiquement.
Le caractère étudié dans l’exemple étant quantitatif, on a bien sûr la représentation graphique des fonctions numériques pour l’illustrer !
Les graphiques qui suivent ont été réalisé avec des donnée modifiées : les notes ont été arrondies au point supérieur.
La série statistique des effectifs cumulés est la fonction qui à chaque modalité associe la somme des effectifs des modalités de valeurs inférieures ou égale à cette modalité.
Exemple à réaliser en exercice à partir des données du tableau:
On peut, pour les effectifs cumulés, réaliser les représentations graphiques du même type que pour les effectifs. Voyons par exemple le polygone des effectifs cumulés, dont l’intérêt est de lire graphiquement un indicateur statistique intéressant: la médiane , qui correspond à la valeur du caractère dont l’effectif cumulé rassemble 50 % de l’effectif total.
Ici 50 % de l’effectif total correspond à un effectif cumulé de: .
Par lecture graphique, confirmée par la lecture du tableau, la médiane de cette série statistique est située aux alentours de 8 : c’est l’abscisse du point du graphique dont l’ordonnée est 17,5.
Voyons cela de façon plus détaillée par une définition plus précise :
>La médiane d’une série statistique est la valeur centrale de la série statistique : Il y a autant d’effectif avant la médiane qu’après, c’est à dire que les modalités inférieures à la médiane correspondent à 50 % de l’effectif total et les modalités supérieures à la médiane correspondent aux autres 50 % de l’effectif total. C’est pour cela que la médiane est peu sensible aux valeurs extrêmes, ce qui n’est pas le cas de la moyenne !
Méthode :
On ordonne la série des observations par ordre croissant.
Si l’effectif total de la série est impair (de taille: 2n + 1), la médiane est la valeur du terme de rang n + 1 dans cette série ordonnée.
Si l’effectif total de la série est pair (de taille: 2n), la médiane est la moyenne des valeurs des termes de rang n et n + 1 dans cette série ordonnée.
Dans notre exemple, l’effectif total est impair: . La médiane est donc la 18ème note rangée dans l’ordre croissant, c’est à dire: 8.
Remarque :
La médiane d’une série statistique n’est pas à confondre avec la moyenne de cette série!
La médiane partage l’effectif total en 2 classes de même effectif, alors que cela n’est en général pas le cas pour la moyenne !
La série statistique des fréquences est la fonction qui, à chaque valeur du caractère, associe la fréquence de la classe de ce caractère.
Exemple:
Réaliser ceci en exercice à partir des données arrondies au point supérieur:
La série statistique des fréquences cumulées est la fonction qui, à chaque valeur du caractère, associe la fréquence cumulée de la classe de ce caractère.(Même méthode que pour les effectifs cumulés)
Exemple:
Réaliser ceci en exercice à partir des données arrondies au point supérieur.
Si le caractère étudié est défini par :
La population a pour effectif total:
La moyenne de cette série statistique est le nombre défini par:
Exercice:
1. Calculer la moyenne des notes à partir des données d’origine (arrondies au demi-point supérieur), puis avec celles arrondies au point supérieur. Comparer les résultats obtenus.
2. Écrire et effectuer à nouveau le calcul de la moyenne avec la formule utilisant les fréquences:
3. Comparer la moyenne et la médiane. Qu’en pensez-vous ?
Télécharger puis imprimer cette fiche en PDF.
Télécharger ou imprimer cette fiche «statistiques : cours de maths en 2de en PDF.» au format PDF afin de pouvoir travailler en totale autonomie.
Réviser les cours et exercices avec nos Q.C.M :
D'autres ressources pour progresser en autonomie :
