Fonctions avec variations et résolution d'équations: cours en 2de

sommaire

1 I. Rappels et compléments sur les fonctions numériques
- 1.1 1.Notion de fonction
- 1.2 2. Représentation graphique des fonctions
2 II. Résolution graphique d’équations :
- 2.1 1. Equation du type f (x) = k (avec k un nombre réel)
3 III-Notion de variations sur un intervalle

Les fonctions numériques à travers un cours de maths en 2de est toujours essentiel pour la progression de l’élève. Ainsi, vous verrez dans ce cours la définition, le sens de variation et la courbe représentative d’une fonction ainsi que l’étude de son sens de variation. L’élève devra être capable d’étudier une fonction définie soit par son expression algébrique soit par sa courbe représentative. Il doit aussi être en mesure de représenter le tableau de variation et de résoudre graphiquement des équations et des inéquations.

I. Rappels et compléments sur les fonctions numériques

1.Notion de fonction

Définition :

On définit une fonction sur un ensemble $D\subset,\mathbb{R}$ en associant à chaque réel x de D

un unique réel noté f(x).

On note : $f:x,\mapsto ,f(x)$

x est la variable;
f(x) est l’image de x par la fonction f .
Si y = f(x), alors x est l’antécédent de y par f.
D est l’ensemble de définition de la fonction, c’est-à-dire l’ensemble des nombres qui ont une image par f.

Exemples :

Fonction définie sur ℝ par son expression littérale :

Fonction de deux variables :

On appelle x et z la base et la hauteur d’un triangle.

Son aire est donnée par la formule : $A(x,z)=\frac{xz}{2}$ .

Fonction prenant ses valeurs dans ℕ :

On attribue à chaque nombre réel supérieur à 1 le nombre de diviseurs de sa partie entière.

2. Représentation graphique des fonctions

Définition :

La courbe représentative C_f d’une fonction f (ou représentation graphique) est l’ensemble des points du plan de coordonnées ( x ; y ) tels que :

l’abscisse x est une valeur de l’ensemble de définition D;
l’ordonnée y est l’image de x par f. On a donc y = f(x).

Autrement dit $M(x,y)\in\,C_f$ si et seulement si $x\in\,D$ et y = f(x).

Exemple :

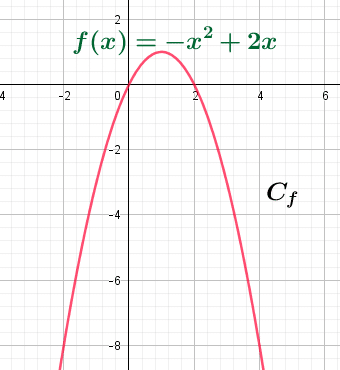
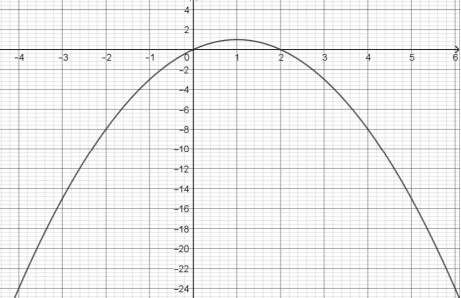
f est la fonction définie sur $\mathbb{R}$ par $f\,(x)=-x^2\,+\,2x$ .

Tracer sa courbe représentative après avoir compléter un tableau de valeurs .

II. Résolution graphique d’équations :

1. Equation du type f (x) = k (avec k un nombre réel)

Propriété :

Les solutions de l’équation f(x) = k sont les abscisses des points d’intersection de la courbe C_f et de la droite horizontale d’équation y=k .

Sur cette courbe représentative de la fonction f, l’équation f(x) = k a pour unique solution le nombre a.

Remarque :

Résoudre l’équation f(x) = g(x), où f et g sont deux fonctions numériques, revient à trouver les coordonnées des points d’intersection de ces deux courbes.

III-Notion de variations sur un intervalle

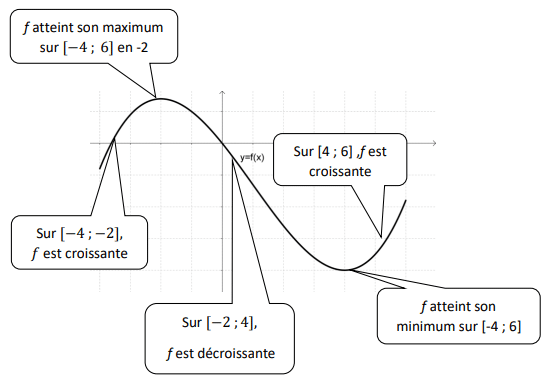
On considère une fonction f représentée sur l’intervalle [−4 ;6] .

Définition :

On dit que la fonction est croissante sur un intervalle lorsque les images de deux nombres quelconques de cet intervalle sont toujours dans le même ordre que les nombres de départ. Graphiquement, la courbe « monte ».

$x\,\leq\,\,\,y\,\Leftrightarrow\,\,f(x)\,\leq\,\,\,f(y)$

Définition :

On dit que la fonction est décroissante sur un intervalle lorsque les images de deux nombres quelconques de cet intervalle sont toujours dans l’ordre contraire de celui des nombres de départ. Graphiquement, la courbe « descend ».

$x\,\leq\,\,\,y\,\Leftrightarrow\,\,f(x)\,\,\geq\,\,\,f(y)$

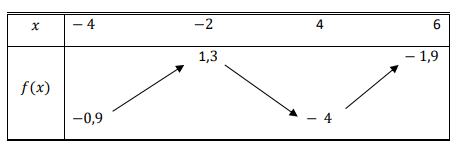
Tableau de variations :

C’est un tableau où on y résume les variations de la fonction :

Vocabulaire :

On appelle « extremum » tout maximum ou minimum de la fonction sur son ensemble de définition.

Exemple :

Tracer une courbe susceptible de représenter la fonction définie sur [−2 ; 4] telle que :

f atteint son maximum sur [−2 ; 4] en 4;

Le point (−2 ; 0) est un point de la courbe de f;

Un antécédent de 4 est 3 par f;

L’image de 1 est −0,5 par f.

Le minimum de f sur [−2 ; 4] est −1, atteint en 0;

f (4) = 5;

f est décroissante sur [−2 ; 0] et croissante sur [3,5 ; 4];

3 a deux antécédents par f qui sont x = 2 et x = 3,5.

Télécharger puis imprimer cette fiche en PDF.

Télécharger ou imprimer cette fiche «fonctions avec variations et résolution d'équations : cours de maths en 2de en PDF.» au format PDF afin de pouvoir travailler en totale autonomie.

Réviser les cours et exercices avec nos Q.C.M :

Q.C.M en 6ème Q.C.M en 5ème Q.C.M en 4ème Q.C.M en 3ème Q.C.M en 2de Q.C.M en 1ère Q.C.M en Terminale

D'autres ressources pour progresser en autonomie :

Chronomètre Horloge France Tables Multiplication Arrondir des décimaux Rapporteur et Angles Médiatrice Symétrie Axiale d'un triangle Symétrie Centrale d'un triangle Translation d'un triangle Rotation Homothétie Bissectrice Tracer droite parallèle Conversion Aires et Volumes Addition de deux relatifs Soustraction Relatifs Addition et soustraction de trois relatifs Produit Deux Relatifs Produit Trois Relatifs Quotient Relatifs Carré Entier Racine Carrée Théorème Pythagore Liste Diviseurs Décomposition Facteurs Premiers Calcul du PGCD PGCD Algorithme Euclide Test Nombre Premier Déterminer Fonction Linéaire Déterminer Fonction Affine Traceur Courbe Trigonométrie Angle Trigonométrie Longueur Périmètre d'un Cercle Aire d'un Disque Volume du Parallélépipède Rectangle Volume du cylindre Surface d'une Sphère et Volume d'une boule Volume d'une pyramide à base rectangulaire Section d'une pyramide Visualiser Section Cône en 2D Section d'un Cône Carte Mondiale Coordonnées Géographiques

Mathématiques Web c'est 2 250 077 fiches de cours et d'exercices téléchargées.