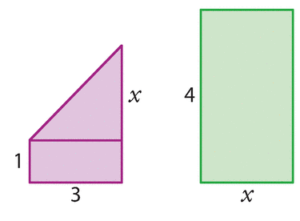Les inéquations : exercices de maths en 3ème corrigés en PDF.

Les inéquations du premier degré à une inconnue avec une série d’exercices de maths en 2de qui vous sera très avantageuse. De plus, vous aurez l’occasion d’acquérir des compétences nouvelles avec ce chapitre.

Ces énoncés corrigés font intervenir les notions suivantes :

définition d’une inéquation du premier degré à une inconnue;
propriétés de résolution des inéquations;
ensemble solution;
résoudre une inéquation;
représentation de l’ensemble solution sur une droite graduée.

Ces énoncés sont à télécharger gratuitement au format PDF.

Exercice 1 :

Résoudre les inéquations suivantes :

$a.5(x-2)\leq\, 4x-2\\ \\ b.-6(2x+2)\geq\, 3x-27$

Exercice 2 :

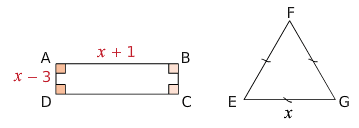
ABCD est un rectangle et EFG est un triangle équilatéral.

x désigne un nombre strictement supérieur à 3.

1.Exprimer le périmètre de ABCD et EFG en fonction de x. Donner la forme réduite.

2.Déterminer les valeurs de x pour lesquelles le périmètre du rectangle est

strictement inférieur à celui du triangle.

Exercice 3 :

Résoudre les inéquations suivantes où x est l’inconnue réelle :
a. 3x < 6
c. -5x < 15
b. 2x>5
d. -7x>28

Exercice 4 :

Résoudre les inéquations suivantes où x est l’inconnue réelle :
a.
b.

Exercice 5 :

Résoudre chaque inéquation.

On notera S l’ensemble des solutions et on représentera S sur l’axe des réels.

a.
b.
c.
d.
e. $6x-5 \geq\, 4x +2$
f. $3x+4\leq\, 4x-4$
g.

Exercice 6 :

Résoudre les inéquations suivantes puis, représenter l’ensemble solution sur une droite graduée.

$a.\,\frac{7}{2}x+\frac{7}{2}>\frac{3}{2}x-\frac{1}{3}$

$b.\,-\frac{3}{7}x+\frac{5}{9}<-\frac{7}{3}x+1$

$c.\,-\frac{2}{3}x+\frac{1}{5} \leq\, \frac{7}{5}x+\frac{2}{7}$

$d.\,\frac{1}{2}x-\frac{1}{3} \geq\, \frac{1}{2}x+2$

Exercice 7 :

Soit a et b deux réels positifs quelconques.
a. Développer $(\sqrt{a}-\sqrt{b})^2$ .
b. En déduire qu’on a toujours $\sqrt{ab}\leq\, \frac{a+b}{2}$
c. Montrer que $\sqrt{ab}=\frac{a+b}{2}$ si et seulement si a = b.
d. Application
Soit p un réel strictement positif.

Déterminer le rectangle d’aire maximale de périmètre p.

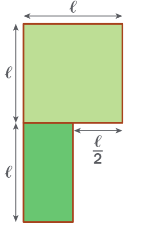
Exercice 8 :

Une agricultrice souhaite clôturer une partie de son domaine en deux zones rectangulaires,

comme sur la figure ci-dessous.

Le passage entre les deux zones est aussi clôturé.
Elle dispose pour cela de 5 330 mètres de fil.
Quelle peut être la valeur maxi male de $\rho$ ?

Exercice 9 :

Un silo à grains est vidé dans un camion à raison de quatre tonnes par minute.

Initialement, ce silo contenait 12 tonnes et 800 kg de grains.
Pendant quel intervalle de temps, à la seconde près, restera-t-il entre 4 et 8 tonnes de
grains dans le silo ?

Exercice 10 :

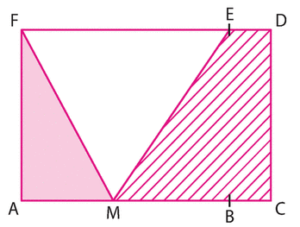
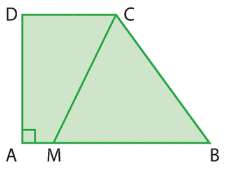
ACDF est un rectangle tel que AC = 6 et AF = 4.
B $\in$ [AC] et E $\in$ [FD] tels que CB = 1 et DE = 1.
M est un point quelconque du segment [AB].
Morgan veut chercher à quelle distance du point A il doit placer le point M
pour que l’aire hachurée soit supérieure ou égale à l’aire du triangle AMF.
Quelle inéquation doit-il poser et résoudre pour répondre à ce problème ?

Exercice 11 :

Tom sait que le bénéfice x (en euros), de sa dernière vente de chocolats est
compris dans l’intervalle [190 ; 200].

De plus, il sait que le bénéfice y de sa dernière vente de jus de pommes est
tel que $56 \leq\, y \leq\, 60$ .

L’année prochaine, il prévoit de multiplier les bénéfices de sa
vente de chocolats par 1,3 et les bénéfices de sa vente de jus de pommes par 1,2.
Déterminer un encadrement de son bénéfice total pour l’année prochaine.

Exercice 12 :

Comparer les aires de ces deux figures.

Exercice 13 :

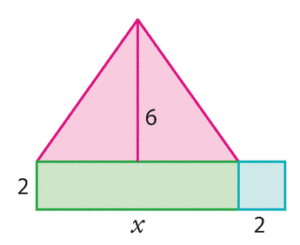
On considère la figure ci-dessous (les longueurs sont en cm).

Déterminer, à l’aide d’une inéquation, les valeurs de x pour
lesquelles l’aire de cette figure est supérieure ou égale à 50 cm².

Exercice 14 :

Assia a acheté un sachet de graines de carottes valant 2,90 euros
pour les semer dans son jardin. Elle compte revendre quelques kilogrammes de carottes à
ses amis au prix de 1,50 euro le kilogramme.
Elle cherche à connaître le nombre de kilogrammes qu’elle
doit vendre pour réaliser un bénéfice supérieur ou égal à 25 euros.

En notant nombre de kilogrammes de carottes à vendre et à l’aide d’une inéquation, déterminer la solution au problème.

Exercice 15 :

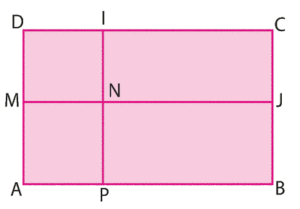
ABCD est un rectangle tel que AB = 5 cm et AD = 3 cm.

M est un point du segment [AD].

On place les points P sur [AB] et N tel que AMNP soit un carré.

Le point I est l’intersection de (PN) et (CD) et J celle de (BC) et (MN).
À quelle distance du point A faut-il placer M pour que l’aire de AMNP
soit supérieure ou égale à l’aire de CJNI ?

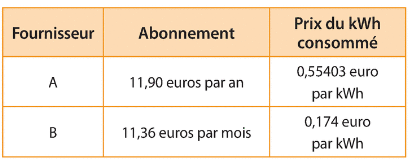
Exercice 16 :

Deux fournisseurs d’électricité donnent les tarifs suivants pour une puissance souscrite de 6 kVA sur leurs sites Internet.

1. Ernest consomme en moyenne 600 kWh par an.
Comparer les offres des deux fournisseurs pour lui.
2. On note x la consommation annuelle en kWh d’électricité d’un client
a) Déterminer en fonction de x le prix annuel payé au fournisseur A.
b) Déterminer à l’aide d’une inéquation les valeurs de x pour lesquelles le fournisseur A est plus intéressant que le fournisseur B.
c) Comparer suivant les valeurs de x les offres de ces deux fournisseurs.

Exercice 17 :

Un pré est représenté par un trapèze rectangle ABCD tel que AB = 12, AD = 8 et DC = 5, en dam.

On souhaite partager ce pré par un segment [CM], où M est
un point du segment [AB], en deux parcelles ADCM et CBM.
1.Soit . À quel intervalle appartient ?
2.a) Exprimer en fonction de AM l’aire de ADCM.
b) Encadrer la valeur de l’aire de ADCM si $O \leq\, AM \leq\, 3$ .
3. Déterminer à l’aide d’une inéquation les valeurs de pour
lesquelles l’aire de ADCM est supérieure à celle de CBM.

Télécharger puis imprimer cette fiche en PDF.

Télécharger ou imprimer cette fiche «les inéquations : exercices de maths en 2de corrigés en PDF.» au format PDF afin de pouvoir travailler en totale autonomie.

Vous devez vous inscrire ou vous connecter à votre compte afin de pouvoir télécharger ce document au format PDF.

D'autres cours et exercices à consulter

Mathématiques Web c'est 2 268 671 fiches de cours et d'exercices téléchargées.