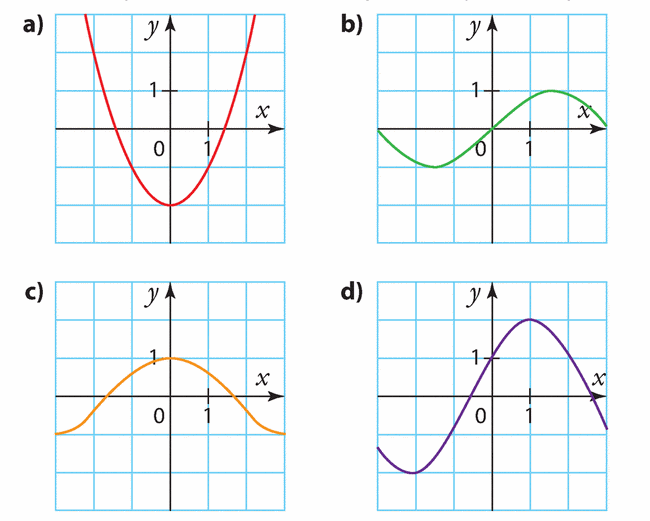Les inéquations et tableaux de signes : exercices de maths en 2de.

Les inéquations et les tableaux de signes à travers des exercices de maths en 2de corrigés. En effet, ce chapitre englobe des connaissances assez pratiques et générales. Une fois que l’élève parvient à bien les comprendre et les traiter, cela devient un jeu d’enfant pour lui. L’élève devra savoir résoudre des inéquations soit par le calcul, en appliquant les propriétés qui permettent de modifier les inégalités sans en méfier l’ensemble solution, soit la résoudre graphiquement en exploitant le tableau de variation ou en créant un tableau de signes. Ces énoncés disposent de leur correction et vous permettent, par conséquent, de vous auto-corriger afin de réussir votre année de seconde.

Exercice 1 :

Résoudre dans R :

1) 2 x – 5 < 3 x – 7

2) $\frac{1+4x}{1-4x}=\frac{1-4x}{1+4x}$

3) x² + x + $\frac{1}{4}$ < (2 x + 1)²

Exercice 2 :

1) Démontrer que pour tout réel x, on a $x^2-x= ( x-\frac{1}{2} )^2-\frac{1}{4}$ .

2) Soient deux réels x et y tels que x + y = 1, démontrer que :

a) x y < $\frac{1}{4}$ b) x² + y² > $\frac{1}{2}$

Exercice 3:

Déterminer le signe des expressions suivantes :

a) x² + 1	b) – $\sqrt{x}$	c) (x – 1)² + 4	d) –x² – 7
e) –(–x – 2)²	f) 1 + $\frac{4}{x^2}$	g) $\sqrt{x^2+1}+3$

Exercice 4 :

Dresser, dans chacun des cas suivants, le tableau de signes de A(x).

a) A(x) s’annule en 5 et –2 ; A(x) est strictement positif pour x supérieur à 5 ou inférieur à –2 et A(x) < 0 sur ]–2 ; 5[.

b) A(x) ≤ 0 pour x $\in$ [–3 ; 4] et A(x) ≥ 0 pour x $\in$ ]– $\infty$ ; –3] $\cup$ [4 ; + $\infty$ [.

c) A(x) n’existe pas en –1 ; le réel 3 est l’unique solution de l’équation A(x) = 0 et A(x) ≥ 0 sur ]– $\infty$ ; –1[ $\cup$ ]–1 ; 3] et A(x) est négatif pour x ≥ 3.

Exercice 5 :

Étudier le signe des expressions suivantes dans un tableau de signes.

a) (5x – 1)(1 – x) b) (3x + 4)(2x + 3) c) 3x(x – 2)

d) (2x + 1)(–5 – x)(x – 7) e) $\frac{4-x}{2+x}$ f) $\frac{-5}{x(x-1)}$

Exercice 6:

Étudier le signe des expressions suivantes après avoir factorisé ou mis au même dénominateur.

a) (2x – 1)(2 + x) – (2x – 1)² b) x² – (2x + 1)² c) $\frac{x}{x+4}-2$

Exercice 7 :

1/ Déterminer une expression f(x) dont le tableau de signes est :

x	– $\infty$		–2		3		+ $\infty$
signe de f(x)		+	0	–	0	+

2/ Déterminer une expression g(x) dont le tableau de signes est :

x	– $\infty$		1		4		+ $\infty$
signe de g(x)		–	║	+	0	–

Exercice 8:

L’étude du signe de l’expression B(x) a permis d’établir le tableau ci-dessous :

x	– $\infty$		–2		1		3		+ $\infty$
signe de B(x)		–	0	+	║	+	0	–

Les affirmations suivantes sont-elles vraies ?

a) B(4,5) est négatif. b) B(1) = 0

c) –2 et 3 sont les solutions de l’équation B(x) = 0.

d) B(0) > 0 e) Si x < 0 alors B(x) < 0.

f) L’ensemble des solutions de B(x) ≤ 0 est ]– $\infty$ ; –2] $\cup$ [3 ; + $\infty$ [.

g) Les nombres tels que B(x) > 0 sont les nombres vérifiant –2 ≤ x ≤ 3.

Exercice 9 :

Résoudre les inéquations suivantes :

a) (2x – 5)(–x – 3) ≥ 0 b) (x – 4)(2x + 3) + (x – 4)(x – 7) ≤ 0

c) (2x – 5)(–x – 3) ≤ –15 d) (x + 1)² > (2x – 3)²

e) $\frac{3x-1}{2-x}$ ≤ 0 f) $\frac{4x-7}{3x+2}$ < 4

g) (–x + 1)(6x – 5)(x + 3) + (–x + 1)(6x – 5)(x – 5) > 0

Exercice 10 :

Soit f et g les fonctions définies sur par f(x) = x² et g(x) = 4x – 3

1/ a) Tracer les courbes représentant ces deux fonctions sur l’écran de la calculatrice.

b) En déduire l’ensemble des solutions de l’inéquation f(x) ≥ g(x).

2/ a) Développer (x – 1)(x – 3).

b) Résoudre, par le calcul cette fois, f(x) ≥ g(x).

Exercice 11 :

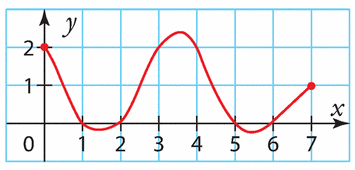
Voici la courbe représentative d’une fonction f définie sur [0;7].
Estimer les solutions des équations suivantes.
a) f(x)=2 b) f(x) = 0 c) f(x) =- 1 d) f(x) = 1

Exercice 12:

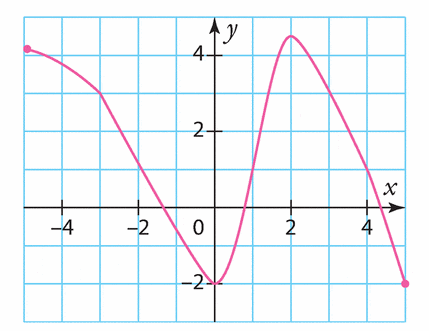
Voici la courbe représentative d’une fonction g définie sur [—5 ; 5].
Estimer les solutions des équations.
a) g(x) = 2
b) g(x) = —3
c) g(x) = 4
d) g(x) =- 1

Exercice 13 :

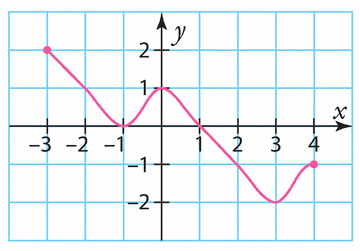
Voici la courbe représentative d’une fonction k définie sur [ – 3 ; 4].
Estimer les solutions des équations et inéquations suivantes.
a) k(x) = 1

b) k(x) = 0
c) k(x) > – 1

d) k(x) < 0
e) $k(x)\geq\, - 2$

f) $k(x)\geq\, 2$

Exercice 14:

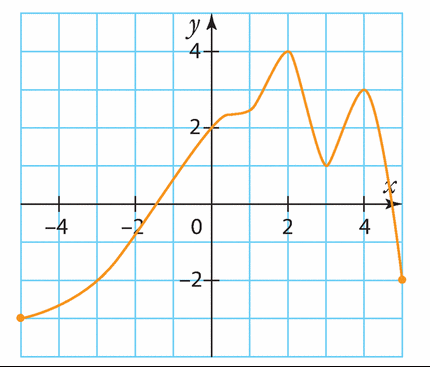
Voici la courbe représentative d’une fonction h définie sur [—5 ; 5].
Estimer les solutions des inéquations suivantes.
a) $h(x) \geq\, 0$
b) h(x) < —4
c) h(x) < —2
d) h(x) > 2

Exercice 15:

Voici les courbes représentatives d’une fonction f et d’une fonction g définies sur [ – 2 ; 3].
Résoudre graphiquement les équations et inéquations.
a) g(x) = f(x)
b) $g(x) \leq\, f(x)$
c) f(x) < —3
d) g(x) < 2
e) $f(x) \geq\, -2$

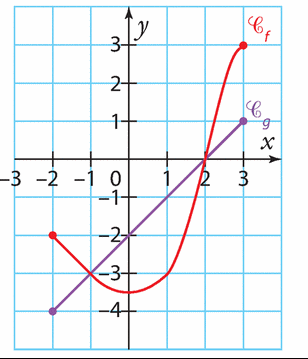
Exercice 16 :

Voici les courbes représentatives de deux fonctions f et g définies sur [—4 ; 3].
Résoudre graphiquement les équations et inéquations suivantes.
a) f(x) = 8

b) f(x) < 0
c) f(x) = g(x)
d) $f(x)\leq\, g(x)$

Exercice 17 :

Pour chacune des courbes ci-dessous, dire si elle semble être la courbe représentative d’une fonction paire, d’une fonction impaire ou d’une fonction qui n’est ni paire ni impaire.

Exercice 18 :

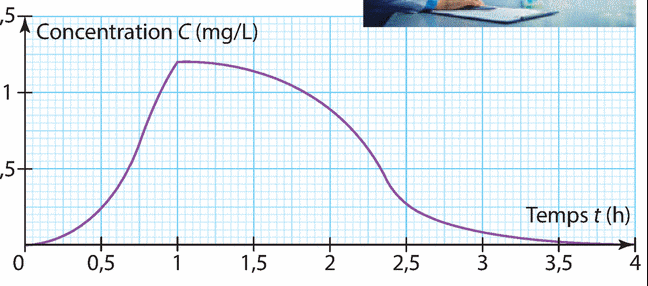
On a mesuré en continu pendant quatre heures, la concentration C d’un médicament dans le sang d’un
patient. La fonction C est représentée ci-dessous.
1. Quelle est Ia concentration du médicament dans le sang au bout de 2h ?
a) environ 0,5 b) environ 1
c) environ 1.5 d) environ 0,9

2. Laquelle (lesquelles) de(s) (in)équations suivantes a pour solution l’intervalle de temps où la concentration du
médicament est au plus égale à 1 ?

a) C(t)>1 b) C(t)=1
c) C(t)<1 d) C(t) $\leq\,$ 1
3. Au bout de combien de temps la concentration dans le sang est-elle égale à 0.5 mg/L ?

a) $\approx$ 40 min b) $\approx$ 2 h 20 min c) $\approx$ 0,667 h
4. Ce médicament est jugé efficace quand la concentration dans le sang dépasse 0.75 mg/L.
Quelle est donc sa période d’efficacité ? (Arrondir grossièrement.)
a) jusqu’à 2 h b) jusqu’à 4h
c) dès 45 min d) entre 0,75 h et 2,2 h

5. Au de combien de temps le médicament est-il le plus concentré ?

a) $\approx$ 1h b) $\approx$ 1 h 30 min c) $\approx$ 1 h 50 min d) $\approx$ 6h

6. Quelle est alors Ia concentration du médicament dans le sang en mg/L ?
a) $\approx$ 1 b) $\approx$ 1,2 c) $\approx$ 1,25 d) $\approx$ 5.8

Exercice 19 :

Une fonction f a les propriétés suivantes :
— elle est définie sur [0 ; 8] ;
— l’équation f(x) = 3 a deux solutions : 1 et 3 ;
— l’image de 0 est 1 ;
— l’inéquation $f(x)\leq\, 0$ a pour ensemble de solution [5 ; 7].
Tracer dans un repère une courbe possible pour la fonction f.

Exercice 20 :

Trouver les coordonnées du ou des points d’intersection des courbes d’équations et .
Même question pour les courbes d’équations $y=\frac{1}{x}$ et $y=\frac{2+3x}{x}$ .

Exercice 21:

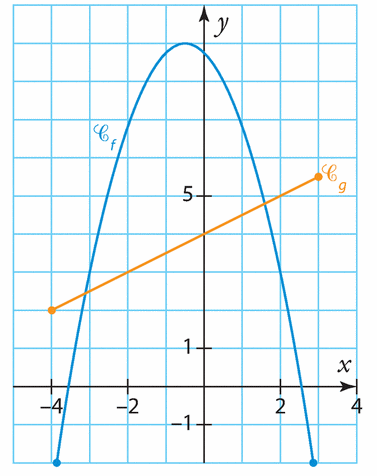
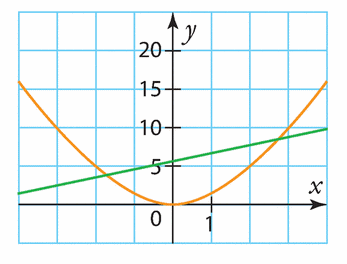
On considère les courbes représentatives de la fonction carré, notée f, et de la fonction affine g définie sur $\mathbb{R}$ par $g(x)\,=\,x\,+\,6$ .
Elles sont tracées dans le repère ci-dessous.
1. Repérer les courbes associées aux deux fonctions.
2. Résoudre graphiquement l’équation .
3. a) Développer l’expression .
b) Retrouver algébriquement les résultats obtenus la question 2.

Exercice 22 :

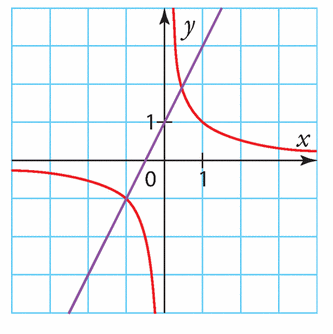
On considère les courbes représentatives de la fonction inverse, notée f, et
de la fonction affine g définie sur $\mathbb{R}$ par g(x) = 2x+ 1.

Elles sont tracées dans le repère ci-dessous.
1. Repérer les courbes associées aux deux fonctions.
2. Résoudre graphiquement l’équation $\frac{1}{x}=2x+1$ .
3.a) Développer l’expression .
b) Retrouver algébriquement les résultats obtenus à la question 2.

Exercice 23:

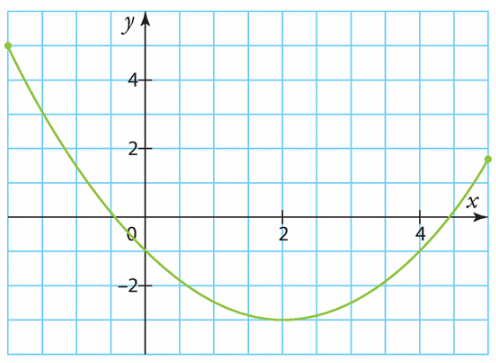
On donne ci-dessous la courbe représentative de la fonction f définie sur [—2 ; 5] par .

1. Estimer graphiquement les deux solutions de l’équation f(x) = 1.
2. Voici un tableau de valeurs de la fonction f.

a) Donner un encadrement d’une des solutions de l’équation f(x) = 1.
b) Quelle est la précision de cette approximation ?
3. A l’aide de la calculatrice, donner un encadrement au dixième près, puis au centième près de l’autre solution.

Télécharger puis imprimer cette fiche en PDF.

Télécharger ou imprimer cette fiche «les inéquations et tableaux de signes : exercices de maths en 2de corrigés en PDF.» au format PDF afin de pouvoir travailler en totale autonomie.

Réviser les cours et exercices avec nos Q.C.M :

Q.C.M en 6ème Q.C.M en 5ème Q.C.M en 4ème Q.C.M en 3ème Q.C.M en 2de Q.C.M en 1ère Q.C.M en Terminale

Mathématiques Web c'est 2 266 531 fiches de cours et d'exercices téléchargées.

Réviser les cours et exercices avec nos Q.C.M :

D'autres cours et exercices corrigés à consulter :