Les équations : exercices de maths en 2de corrigés en PDF.

Les équations du premier degré à une inconnue à travers des exercices de maths en 2de corrigés. L’élève devra connaître les propriétés qui permettent de modifier les égalités sans en changer l’ensemble solution. Ces énoncés disposent de leur correction afin que vous puissiez réviser en ligne et vous auto-corriger.

Exercice 1 :

$(E_1)\,:\,(0,1\,x\,-\,1)(0,2\,x\,-\,2)(0,3\,x-\,3)(0,04\,x-0,4)\,=\,0$

(E2) : $\frac{2x+3}{5x-1}$ = 2

(E3) : 4 x − 0,8 = 2 − 1,6 x

(E4) : $\frac{3}{x}$ = $\frac{x}{5}$

(E5) : (x − 2)² = $\frac{1}{16}$ (5 − 2 x)²

(E6) : $\frac{x-4}{x-2}=\frac{x+2}{x}$

(E7) : (x + 1)(3 − 2 x) = 4 x² − 9

(E8) : $\frac{x^2}{1-2x}$ = −1

(E9) : (x + 2)² = 2(x² − 4)

(E10) : $\frac{x^2+x+1}{2x-3}\,=\frac{1}{2}$

Exercice 2 :

Résoudre dans $\mathbb{R}$ les équations suivantes :

a) $\frac{1-x }{4}-\frac{3x-2 }{2}=\frac{2x+5 }{6}$

(On montrera que cette équation est équivalente à : )

c) $3x-1=\frac{4}{3x-1}$

(On montrera que cette équation est équivalente à : $\frac{(3x-3)(3x+1) }{3x-1}=0$ .

Exercice 3 :

Factoriser en utilisant une identité remarquable.

Exercice 4 :

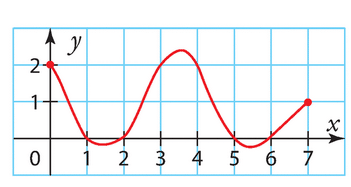
Voici la courbe représentative d’une fonction f définie sur [0;7].

Estimer les solutions des équations suivantes.

a) f(x)= 2 b) f(x) = 0 c) f(x) = – 1 d) f(x) = 1.

Exercice 5 :

Pour chacune des fonctions dont on donne les expressions ci-dessous,

essayer d’établir le plus grand ensemble de définition possible.

$a)f(x)=\frac{5+x}{10-x}$ $b)g(x)=2\sqrt{x}+3$

$c)h(x)=\frac{3x+x^2}{2}$ $d)i(x)=4x+\frac{1}{x}$

Exercice 6 :

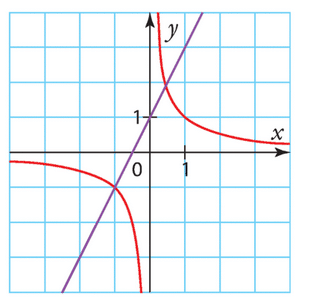
On considère les courbes représentatives de la fonction inverse, notée f, et

de la fonction affine g définie x sur R par g(x) = 2x + 1.

Elles sont tracées dans le repère ci-dessous.

1. Repérer les courbes associées aux deux fonctions.

2. Résoudre graphiquement l’équation $\frac{1}{x}= 2x +1$ .

3. a) Développer l’expression (2x – 1)(x+ 1).
b) Retrouver algébriquement les résultats obtenus à la question 2.

Exercice 7 :

Les équivalences suivantes sont-elles vraies ou fausses ? (On justifiera, et si l’équivalence est fausse, on ajoutera à l’équation de droite ce qu’il faut pour qu’elle devienne équivalente à l’équation de gauche)

1) $(x\,+\,5)(x\,+\,1)\,=\,(3\,x-\,2)(x\,+\,1)$ $\Leftrightarrow$ $x\,+\,5\,=\,3\,x-\,2$

2) $(x\,+\,3)(x^2\,+\,1)\,=\,(x^2\,+\,1)(4\,x-1)$ $\Leftrightarrow$ $x\,+\,3\,=\,4\,x-1$

3) $(2\,x-3)^2\,=\,(3\,x-1)^2$ $\Leftrightarrow$ $2\,x-3\,=\,3\,x-1$

Exercice 8 :

Résoudre dans $\mathbb{R}$ les équations suivantes.

$b)\,(2x+3)(4x-5)=0$

Exercice 9 :

Résoudre dans $\mathbb{R}$ les équations suivantes.

Exercice 10 :

Résoudre dans $\mathbb{R}$ les équations suivantes.

Exercice 11 :

Résoudre dans $\mathbb{R}$ les équations suivantes.

Exercice 12 :

Résoudre dans $\mathbb{R}$ les équations suivantes.

$a)\sqrt{x}=12$ $b)\,\sqrt{x}=-2$

$c) \sqrt{x}=11,5$ $d)3\sqrt{x}=21$

Exercice 13 :

Résoudre dans $\mathbb{R}$ les équations suivantes.

$a)\frac{2x-1}{x+6}=1$ $b)\frac{4}{2x+6}=9$

$c)\frac{2x}{x-4}=-3$ $d)\frac{x+1}{x-1}=\frac{1}{2}$

Exercice 14 :

On étudie dans un certain milieu l’évolution d’une population de bactéries.
Le nombre de bactéries en milliers a été modélisé en fonction du temps
écoulé en jours sur les dix premiers jours d’étude par la fonction N définie
par $N(t)=(0,5t+\,1)^2$ pour tout nombre réel $t \in [0;10]$ .

Donner une estimation du nombre de bactéries au bout d’un jour.

Au bout de combien de temps le nombre de bactéries a-t-il atteint 16 000 ?

Exercice 15 équations :

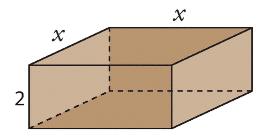
On veut construire une boîte en bois avec couvercle ayant une base carrée de côté et
une hauteur égale à 2.

1. Montrer que la surface extérieure de la boîte est donnée

en fonction de par la formule .

2. Pour quelle(s) valeur(s) de la boîte a t-elle une surface extérieure égale à 72?

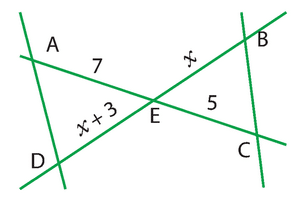
Exercice 16 équations :

Pour quelle(s) valeur(s) de x les droites (AB) et (CD) sont-elles parallèles ?

Exercice 17 équations :

Soient x et y deux réel tels que

On pose

1) Calculer A pour $x\,=\,0$ puis $x\,=-2$ .

2) Développer $(x\,+\,y)^2-2xy$ .
En déduire une simplification de A puis montrer que si $x\,+\,y\,=\,1$ alors A=-1 .

Voir Exercices 11 à 17...

Télécharger puis imprimer cette fiche en PDF.

Télécharger ou imprimer cette fiche «les équations : exercices de maths en 2de corrigés en PDF.» au format PDF afin de pouvoir travailler en totale autonomie.

Vous devez vous inscrire ou vous connecter à votre compte afin de pouvoir télécharger ce document au format PDF.

Réviser les cours et exercices avec nos Q.C.M :

Q.C.M en 6ème Q.C.M en 5ème Q.C.M en 4ème Q.C.M en 3ème Q.C.M en 2de Q.C.M en 1ère Q.C.M en Terminale

D'autres ressources pour progresser en autonomie :

Chronomètre Horloge France Tables Multiplication Arrondir des décimaux Rapporteur et Angles Médiatrice Symétrie Axiale d'un triangle Symétrie Centrale d'un triangle Translation d'un triangle Rotation Homothétie Bissectrice Tracer droite parallèle Conversion Aires et Volumes Addition de deux relatifs Soustraction Relatifs Addition et soustraction de trois relatifs Produit Deux Relatifs Produit Trois Relatifs Quotient Relatifs Carré Entier Racine Carrée Théorème Pythagore Liste Diviseurs Décomposition Facteurs Premiers Calcul du PGCD PGCD Algorithme Euclide Test Nombre Premier Déterminer Fonction Linéaire Déterminer Fonction Affine Traceur Courbe Trigonométrie Angle Trigonométrie Longueur Périmètre d'un Cercle Aire d'un Disque Volume du Parallélépipède Rectangle Volume du cylindre Surface d'une Sphère et Volume d'une boule Volume d'une pyramide à base rectangulaire Section d'une pyramide Visualiser Section Cône en 2D Section d'un Cône Carte Mondiale Coordonnées Géographiques

Mathématiques Web c'est 2 250 275 fiches de cours et d'exercices téléchargées.