Exercice 1 :
Lors du deuxième trimestre, un élève a une moyenne de m = 11 après les quatre premiers contrôles. Tous les contrôles du trimestre ont le même coefficient.
1. Cet élève obtient la note de 13 au cinquième contrôle.
Quelle est la nouvelle moyenne m1 ? justifier la réponse par un calcul.
2. L’élève effectue alors un sixième contrôle qui lui permet d’obtenir une moyenne m2 = 12. Quelle est cette sixième note ? justifier la réponse.
3. La moyenne des six contrôles du deuxième trimestre est donc de 12.
Sachant qu’au premier trimestre, il y avait eu quatre contrôles et que la moyenne de l’élève était de 11,5 , quelle est la moyenne des 10 contrôles des deux trimestres ? justifier la réponse.
4. On décide d’augmenter chaque note des quatre contrôles du premier trimestre de 1. De combien augmente la moyenne des contrôles des deux trimestres ? justifier la réponse.
Exercice 2 :
La capacité vitale est le volume d’air maximal pouvant être mobilisé en une seule inspiration.
Sur un échantillon de 17 personnes, on a mesuré la capacité vitale (en litres). Voici la liste des résultats :
4,15 – 4,48 – 5,24 – 4,8 – 4,95 – 4,05 – 4,3 – 4,7 – 5,51 – 4,58 – 4,12 – 5,7 – 4,85 – 5,05 – 4,65 – 4,7 – 4,28.
1. Déterminer la moyenne m de cette série. Arrondir la moyenne au centilitre près.(Pour la moyenne, on écrira le détail du calcul )
2. En expliquant la méthode utilisée, déterminer la médiane de cette série.
3. On décide de regrouper les valeurs de la série par classes.
Compléter le tableau suivant :
| capacité vitale (en litres) |
[4 ; 4,5[ |
[4,5 ; 5[ |
[5 ; 5,5[ |
[5,5 ; 6[ |
| effectifs | ||||
| effectifs cumulés croissants |
4. a) A l’aide de cette répartition par classes, déterminer la moyenne m‘
b) On admet que dans chaque classe, la répartition est uniforme.
Tracer alors le polygone des effectifs cumulés.
En déduire graphiquement le médiane de ces valeurs.
Exercice 3 :
Le tableau suivant donne la distance entre le domicile et le lycée pour 100 élèves d’un lycée.
|
Distance en km |
[0 ; 2[ |
[2 ; 6[ |
[6 ; 12[ |
[12 ; 17[ |
|
Nombre d’élèves |
22 |
28 |
30 |
20 |
1. Déterminer la population, la variable étudiée et sa nature.
2. Représenter cette série statistique par un histogramme.(Un carreau représentera un individu.)
3.Déterminer une valeur approchée de la distance moyenne parcourue par un
élève.(Arrondir au dixième de km)
4. vrai ou faux ? : « 80% des élèves parcourent moins de 12 km » Justifier
5.Dans l’ordre croissant le 50ieme élève parcourt 5,8 km et le51ieme 6,4 km
Que vaut alors la distance médiane ? Justifier.
Exercice 4 :
Dans un grand parc naturel on a recensé les animaux présents.
Voici les résultats :
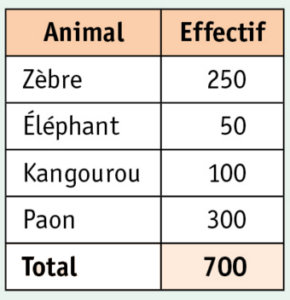
On donnera les résultats sous forme de fractions.
Quelle est la proportion :
a. de zèbres parmi les animaux du parc ?
b. de kangourous parmi les animaux du parc ?
c. de kangourous parmi les animaux du parc se déplaçant
sur deux pattes ?
d. d’éléphants parmi les animaux du parc se déplaçant sur quatre pattes ?
Exercice 5 :
Une enquête est réalisée auprès de 1 500 élèves du lycée qui possèdent un smartphone afin de connaître le type de forfait internet et le débit dont ils disposent.
On a dénombré 210 élèves ayant accès à la 5G et parmi eux 20 % ont un forfait Internet bloqué.
375 élèves ont un forfait Internet illimité.
1. Résumer les données de l’énoncé dans un tableau :
2.Quelle est la proportion d’élèves :
a. ayant un forfait Internet bloqué parmi l’ensemble des élèves ?
b. ayant un accès 5G parmi les élèves ayant un forfait Internet non bloqué ?
3.Quel est le pourcentage d’élèves ayant un forfait Internet bloqué parmi l’ensemble des élèves du lycée ?
Exercice 6 :
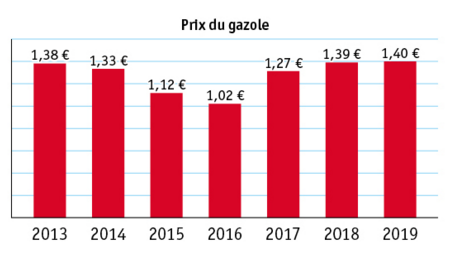
On a relevé le prix du gazole à une pompe à Manosque au 1er janvier de chaque année.
On a obtenu les résultats suivants :
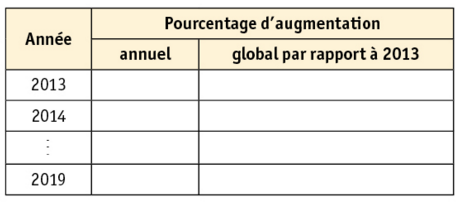
1. Compléter le tableau suivant :
2.En janvier 2020 le prix aura augmenté de 7,65 % par rapport à 2019.
Calculer le prix en 2020.
Exercice 7 :
Un producteur viticole fait le bilan de sa production et de
ses ventes. Il a pu établir le diagramme ci-dessous :
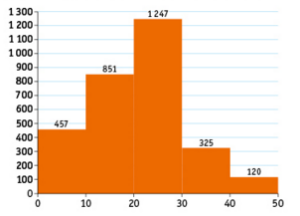
Les prix des bouteilles sont regroupés par tranches ; ainsi par exemple,
il y a 1247 bouteilles vendues dont les prix sont compris entre 20 € et 30 €. Dans les calculs qui suivront, le prix de référence de 25 € désignera les bouteilles dont le prix appartient à l’intervalle [20 ; 30[ (on utilisera la même convention pour les autres intervalles).
1. À l’aide calculatrice, déterminer le prix moyen et l’écart de cette série statistique.
2. Quel est son chiffre d’affaires c’est-à-dire le montant total de ses ventes ?
3. Le viticulteur souhaite diminuer les écarts de prix mais pas son chiffre d’affaires.
Il décide d’augmenter de 10€ les bouteilles dont le prix appartient à [0 ; 10[ et de diminuer
le prix de 10 € pour les bouteilles dont le prix appartient à [40 ; 50{.
a. Déterminer le nouveau prix moyen et l’écart type avec ces nouvelles valeurs.
b. Les souhaits du viticulteur sont-ils réalisés ?
Exercice 8 :
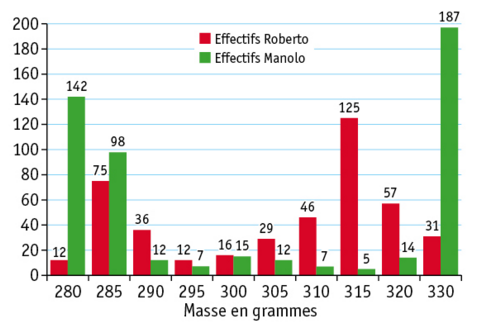
Manolo et Roberto reviennent de la pêche.
Après la pesée de leurs soles ils obtiennent les résultats suivants :
a. Calculer pour chacune de ces séries statistiques la masse moyenne des soles.
b. Quel est l’écart type de chacune de ces deux séries statistiques ?
Comment peut-on interpréter ces deux valeurs ?
c. Donner l’écart interquartile de chacune de ces deux séries statistiques.
Ces deux valeurs confirment-elles les résultats de la question b. ?
d. Quel pêcheur a pris le plus de poisson ?
Exercice 9 :
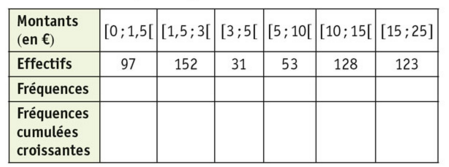
La boulangère se lance dans une étude des montants dépensés par ses clients.
Elle a établi le tableau suivant des montants dépensés par clients :
1. Calculer les fréquences et les fréquences cumulées croissantes.
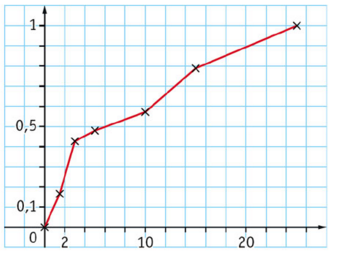
2. On a représenté le graphique des fréquences cumulées croissantes, où en abscisses figurent les montants en C et en ordonnées des fréquences cumulées croissantes :
a. Pour une telle série statistique, la médiane est définie comme étant l’abscisse du point de la courbe ayant pour ordonnée 0,5.
Quelle est la valeur de la médiane ?
b. Le premier quartile est défini comme étant l’abscisse du point de la courbe ayant pour ordonnées 0,25. Lire sur le graphique la valeur de .
c. Comment peut-on déterminer le troisième quartile ?
Faire une phrase pour expliquer et donner sa valeur.
3. La boulangère se propose de faire son bilan comptable.
Compléter son travail en justifiant la réponse.
a. « La moitié de mes clients ont dépensé plus de … €.»
b. « Un quart des clients dépensent moins de … €.»
c.« Le jour de la fête à la viennoiserie, si la boulangère incite tous ses clients à acheter en plus une viennoiserie à 1 € alors la moitié de ses clients aura dépensé au moins … €.»
Exercice 10 :
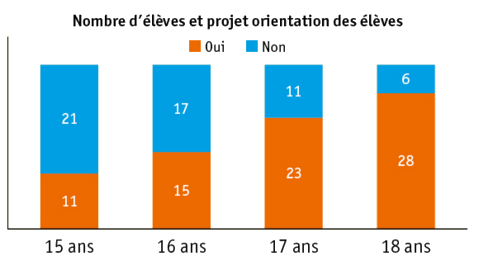
On a fait une étude sur l’orientation des élèves en fonction de leur âge.
On a représenté ci-dessous la répartition des élèves qui ont déjà un projet d’orientation ainsi que
ceux qui n’en ont pas :
Pour chacune des affirmations, dire si elle est vraie ou fausse en argumentant.
a. 58 % de l’ensemble des élèves ont déjà un projet d’orientation.
b. Parmi les 15-16 ans, plus des 3/4 n’ont pas de projet.
c. Parmi les 17-18 ans, plus des 3/4 ont un de projet.
d. Parmi ceux qui n’ont pas de projet, près de 69 % ont 16 ans au moins.
Télécharger ou imprimer cette fiche «les statistiques : exercices de maths en 2de corrigés en PDF.» au format PDF afin de pouvoir travailler en totale autonomie.
Réviser les cours et exercices avec nos Q.C.M :