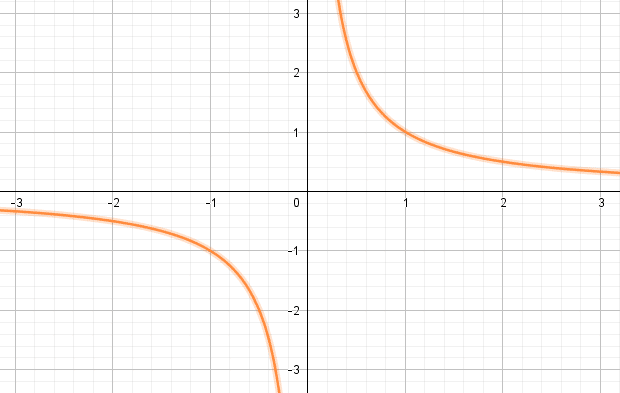Fonctions usuelles : cours de maths en 2de à télécharger en PDF.

sommaire

1 I. Les fonctions linéaires :
2 II. Les fonctions affines :
3 III. La fonction carrée :
- 3.1 1.Définition :
- 3.2 2.Représentation graphique
4 IV. La fonction cube :
- 4.1 1.Définition :
- 4.2 2.Représentation graphique
5 V. La fonction inverse :
- 5.1 1.Définition :
- 5.2 2.Représentation graphique

Les fonctions usuelles à travers un cours de maths en 2de complet qui vous permettra de bien progresser tout au long de l’année. Cette leçon fait intervenir les notions suivantes :

définition d’une fonction numérique;
image et antécédent;
ensemble ou domaine de définition d’une fonction;
fonction affine et linéaire;
fonction carrée;
fonction racine carrée;
fonction inverse;
fonction puissance.

Ce document sur les fonctions usuelles est à télécharger gratuitement au format PDF.

I. Les fonctions linéaires :

1.Définition :

Définition:

On appelle fonction linéaire, toute fonction définie par :

$f:\mathbb{R}\to\,\mathbb{R}\\\,\,\,\,\,\,\,x\,\mapsto \,ax$ où a est un réel donné.

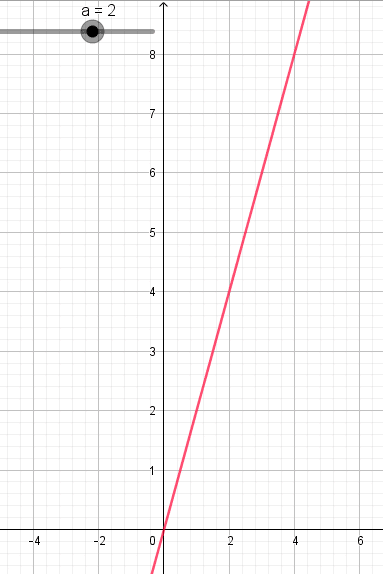
2.Représentation graphique

Propriété :

Dans un repère orthonormé du plan , la représentation graphique d’une fonction linéaire définie sur $\mathbb{R}$ par $f:\mathbb{R}\to\,\mathbb{R}\\\,\,\,\,\,\,\,x\,\mapsto \,ax$ est la droite D d’équation y=ax passant par l’origine du repère (a est un réel donné).

Propriétés :

Si a = 0, la fonction linéaire est la fonction nulle sur $\mathbb{R}$ , nous avons pour tout x, f(x)=0.
Si a>0 , la fonction linéaire est strictement croissante sur $\mathbb{R}$ .
Si a<0 , la fonction linéaire est strictement décroissante sur $\mathbb{R}$ .

3.Propriété caractéristique des fonctions linéaires

Propriété :

Si f est une fonction linéaire, alors quels que soient les réels m et p, le taux de variation entre m et p est constant.

Plus précisément, si , alors, quels que soient les réels m et p : $a=\frac{f(m)-f(p)}{m-p}$ .

Ce nombre a constant est le coefficient directeur de la droite D représentative de la fonction f.

II. Les fonctions affines :

1.Définition :

Définition :

On appelle fonction affine, toute fonction définie par :

$f:\mathbb{R}\to\,\mathbb{R}\\\,\,\,\,\,\,\,x\,\mapsto \,mx+p$ où m et p sont des réels donnés.

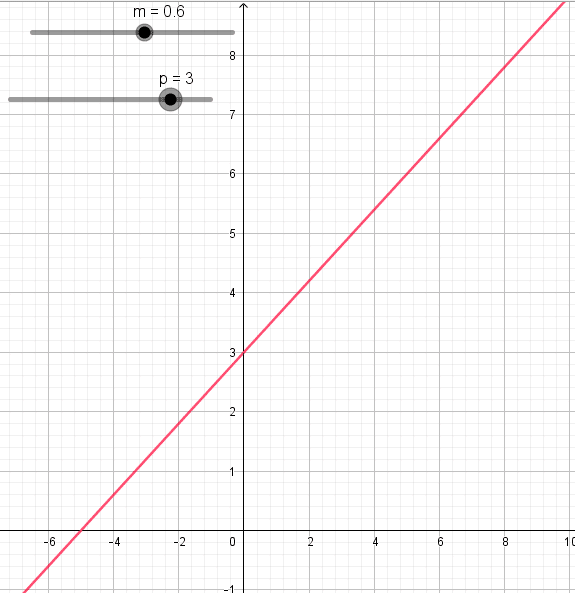
2.Représentation graphique

Propriété :

Dans un repère orthonormé du plan , la représentation graphique d’une fonction affine définie sur $\mathbb{R}$ par $f:\mathbb{R}\to\,\mathbb{R}\\\,\,\,\,\,\,\,x\,\mapsto \,mx+p$ est la droite D d’équation y=mx+p où m et p sont des réels donnés.

Propriété :

Si m = 0, la fonction affine est une fonction constante sur $\mathbb{R}$ , nous avons pour tout x, f(x)=p.
Si m>0 , la fonction affine est strictement croissante sur $\mathbb{R}$ .
Si m<0 , la fonction affine est strictement décroissante sur $\mathbb{R}$ .

3.Propriété caractéristique des fonctions affines

Propriété :

Si f est une fonction affine, alors quels que soient les réels a et b, le taux de variation entre a et b est constant.

Plus précisément, si , alors, quels que soient les réels a et b : $m=\frac{f(b)-f(a)}{b-a}$ .

Ce nombre m constant est le coefficient directeur de la droite D représentative de la fonction f.

Le nombre p est appelé l’ordonnée à l’origine. Nous avons p=f(0).

4.Fonctions affines particulières:

Propriétés :

Si p=0 alors la fonction affine est linéaire.

Dans ce cas f(x) est proportionnel x (m est le coefficient de proportionnalité).

Les graphiques des fonctions linéaires sont des droites qui passent par l’origine du repère . Elles ont pour équation: y=mx.

Si m=0 alors la fonction affine est constante . Nous avons pour tout x, f(x)=p.

Les graphiques des fonctions constantes sont des droites parallèles à l’axe des abscisses . Elles ont pour équation: y=p.

III. La fonction carrée :

1.Définition :

Définition :

On appelle fonction carrée, toute fonction définie par :

$f:\mathbb{R}\to\,\mathbb{R}\\\,\,\,\,\,\,\,x\,\mapsto \,x^2$ .

2.Représentation graphique

Propriétés :

Dans un repère orthonormé du plan , la représentation graphique de la fonction carrée définie sur $\mathbb{R}$ par $f:\mathbb{R}\to\,\mathbb{R}\\\,\,\,\,\,\,\,x\,\mapsto \,x^2$ est la droite parabole d’équation y=x^2 .

Propriété :

La fonction carrée est strictement croissante sur $[0;+\infty[$ .
La fonction carrée est strictement décroissante sur $]-\infty;0]$ .

IV. La fonction cube :

1.Définition :

Définition :

On appelle fonction cube, toute fonction définie par :

$f:\mathbb{R}\to\,\mathbb{R}\\\,\,\,\,\,\,\,x\,\mapsto \,x^3$ .

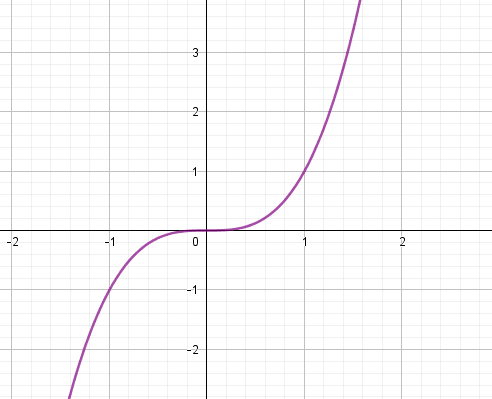
2.Représentation graphique

Propriété :

Dans un repère orthonormé du plan , la représentation graphique de la fonction cube définie sur $\mathbb{R}$ par $f:\mathbb{R}\to\,\mathbb{R}\\\,\,\,\,\,\,\,x\,\mapsto \,x^3$ est la courbe d’équation y=x^3 .

Propriété :

La fonction cube est strictement croissante sur $[0;+\infty[$ .
La fonction cube est strictement croissante sur $]-\infty;0]$ .

V. La fonction inverse :

1.Définition :

Définition :

On appelle fonction inverse, toute fonction définie par :

$f:\mathbb{R^*}\to\,\mathbb{R}\\\,\,\,\,\,\,\,x\,\mapsto \,\frac{1}{x}$ .

2.Représentation graphique

Propriété :

Dans un repère orthonormé du plan , la représentation graphique de la fonction inverse définie sur $\mathbb{R^*}$ par $f:\mathbb{R^*}\to\,\mathbb{R}\\\,\,\,\,\,\,\,x\,\mapsto \,\frac{1}{x}$ est la courbe d’équation $y=\,\frac{1}{x}$ .

Propriété :

La fonction inverse est strictement décroissante sur $[0;+\infty[$ .
La fonction cube est strictement décroissante sur $]-\infty;0]$ .

Télécharger puis imprimer cette fiche en PDF.

Télécharger ou imprimer cette fiche «fonctions usuelles : cours de maths en 2de en PDF.» au format PDF afin de pouvoir travailler en totale autonomie.

Vous devez vous inscrire ou vous connecter à votre compte afin de pouvoir télécharger ce document au format PDF.

Réviser les cours et exercices avec nos Q.C.M :

Q.C.M en 6ème Q.C.M en 5ème Q.C.M en 4ème Q.C.M en 3ème Q.C.M en 2de Q.C.M en 1ère Q.C.M en Terminale

D'autres ressources pour progresser en autonomie :

Chronomètre Horloge France Tables Multiplication Arrondir des décimaux Rapporteur et Angles Médiatrice Symétrie Axiale d'un triangle Symétrie Centrale d'un triangle Translation d'un triangle Rotation Homothétie Bissectrice Tracer droite parallèle Conversion Aires et Volumes Addition de deux relatifs Soustraction Relatifs Addition et soustraction de trois relatifs Produit Deux Relatifs Produit Trois Relatifs Quotient Relatifs Carré Entier Racine Carrée Théorème Pythagore Liste Diviseurs Décomposition Facteurs Premiers Calcul du PGCD PGCD Algorithme Euclide Test Nombre Premier Déterminer Fonction Linéaire Déterminer Fonction Affine Traceur Courbe Trigonométrie Angle Trigonométrie Longueur Périmètre d'un Cercle Aire d'un Disque Volume du Parallélépipède Rectangle Volume du cylindre Surface d'une Sphère et Volume d'une boule Volume d'une pyramide à base rectangulaire Section d'une pyramide Visualiser Section Cône en 2D Section d'un Cône Carte Mondiale Coordonnées Géographiques

Mathématiques Web c'est 2 253 856 fiches de cours et d'exercices téléchargées.