Les fonctions : exercices de maths en 2de corrigés en PDF.

Les fonctions numériques et la lecture graphique d’image et d’antécédents à travers des exercices de maths en 2de et utilisation des définitions et des propriétés en seconde. Vous devrez savoir donner le domaine de définition et savoir étudier les variations d’une fonction par différentes méthodes(tableau de signes ou de variation, calcul littéral ou exploitation de la courbe représentative). Ces énoncés disposent de leur correction ce qui permettra aux élèves de noter ses erreurs afin de pouvoir augmenter ses notes en seconde. Ces énoncés peuvent être téléchargés en PDF gratuitement afin de travailler librement.

Exercice 1 :

Soit f la fonction définie sur $\mathbb{R}$ par $f(x)=-\frac{4}{5}x^2+3x+5$

1)a) Calculer l’image de $1+5\sqrt{2}$ par f , on donnera le résultat sous la forme $a+b\sqrt{2}$ avec a et b deux décimaux .

b) Reprendre la question précédente avec $5-\sqrt{3}$ .

2) Déterminez les antécédents de 5 par f.

3) a)Démontrez que pour tout x réel on a $f(x)=-\frac{4}{5}\,(\,\,(\,x-\frac{15}{8}\,\,)^2-\frac{625}{64}\,\,)$ .

b) En déduire l’expression factorisée de f(x).

c) Déterminez alors les antécédents de 0 par f

Exercice 2 :

On considère la fonction f définie sur $\mathbb{R}$ par:
$f(x)=\frac{4x+2}{1+x^2}$ .

1. A-t-on f(3) = 1 ?
2. Les images de 2 et de 0 par f sont-elles égales ?

3. Déterminer l’image de $\frac{1}{2}$ par f.

4. Déterminer les antécédents de 0 par f.

Exercice 3 :

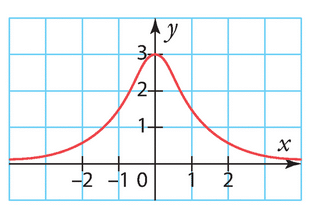
Voici la courbe représentative d’une fonction f définie sur $\mathbb{R}$ .
Par lecture graphique, déterminer :

a) l’image de -1 par f.
b) l’image de 0 par f.
c) le (ou les) antécédent(s) de 1 par f.
d) le (ou les) antécédent(s) de 3 par f.

Exercice 4 :

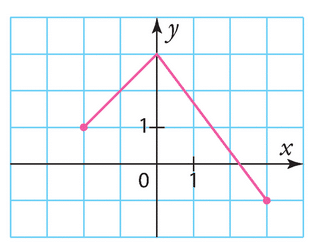
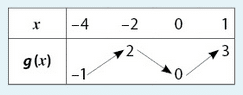
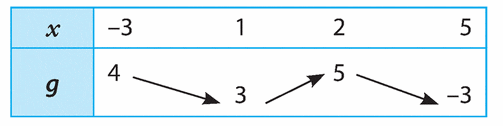
Voici la courbe représentative d’une fonction g définie sur [-2 ; 3].

Par lecture graphique, déterminer :
a) g(0).

b) les images de 1 et -2 par g.

c) les antécédents éventuels de -1 ; 1 et 5.

Exercice 5 :

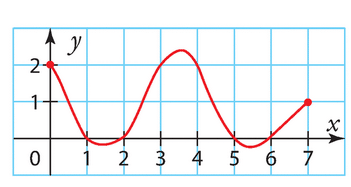
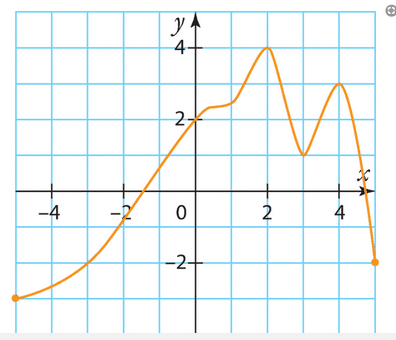
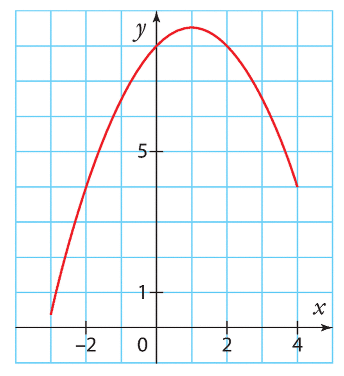
Voici la courbe représentative d’une fonction f définie sur [0;7].

Estimer les solutions des équations suivantes.

a) f(x)= 2 b) f(x)=0 c) f(x) = – 1 d) f(x) = 1.

Exercice 6 :

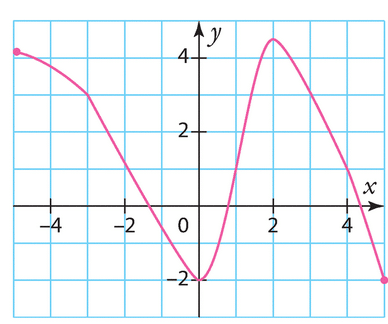
Voici la courbe représentative d’une fonction g définie sur [-5 ; 5].
Estimer les solutions des équations.
a) g(x) = 2.
b) g(x)= -3.
c) g(x) =4.
d) g(x) = -1.

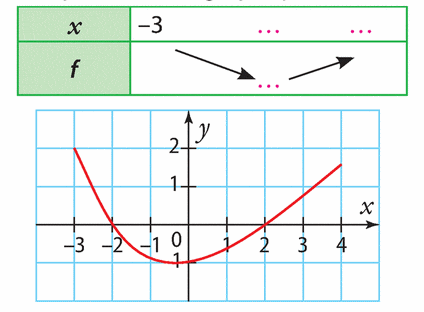
Exercice 7 :

Voici la courbe représentative d’une fonction k définie sur [-3 ; 4].

Estimer les solutions des équations et inéquations suivantes.

a) k(x) =1 b) k(x) = 0 c) k(x)> -1

d) k(x) < 0 e) k(x) $\geq\,$ -2 f) k(x) $\geq\,$ 2

Exercice 8 :

Voici la courbe représentative d’une fonction h définie sur [-5 ; 5].
Estimer les solutions des inéquations suivantes.
a) h(x) $\geq\,$ 0
b) h(x) < -4
c) h(x) < -2
d) h(x) > 2

Exercice 9 :

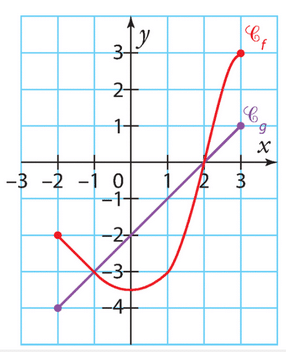
Voici les courbes représentatives d’une fonction f

et d’une fonction g définies sur [-2;3].

Résoudre graphiquement les équations et inéquations.

a) g(x) = f(x)

b) g(x) $\leq\,$ f(x)

c) f(x) < -3

d) g(x) < 2

e) f(x) $\geq\,$ -2

Exercice 10 :

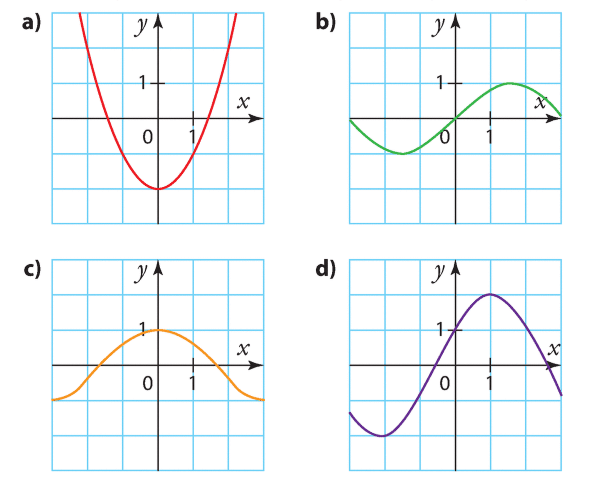
Pour chacune des courbes ci-dessous, dire si elle semble être la courbe représentative d’une fonction paire, d’une fonction impaire ou d’une fonction qui n’est ni paire ni impaire.

Exercice 11 :

Pour chacune des fonctions dont on donne les expressions ci-dessous,

essayer d’établir le plus grand ensemble de définition possible.

$a)f(x)=\frac{5+x}{10-x}$ $b)g(x)=2\sqrt{x}+3$

$c)h(x)=\frac{3x+x^2}{2}$ $d)i(x)=4x+\frac{1}{x}$
Exercice 12 :

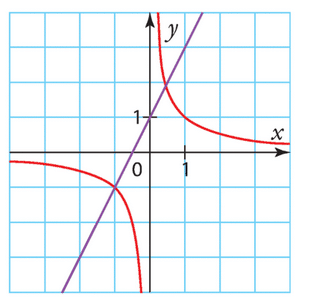
On considère les courbes représentatives de la fonction inverse, notée f,

et de la fonction affine g définie sur R par g(x) = 2x + 1.

Elles sont tracées dans le repère ci-dessous.

1. Repérer les courbes associées aux deux fonctions.

2. Résoudre graphiquement l’équation $\frac{1}{x}=\,2x\,+1$ .
3. a) Développer l’expression (2x – 1)(x+ 1).
b) Retrouver algébriquement les résultats obtenus à la question 2.

Exercice 13 :

On considère une fonction f dont on donne la représentation graphique sur [3;4].

1. Déterminer l’image de 2.

2. Donner la valeur de f(-2).

3. Donner une valeur approchée des antécédents de 5.
4. Résoudre f(x) = 4.

5. Résoudre f(x) < 6.

6. Résoudre f(x) $\geq\,$ 8.

Exercice 14 :

Soit f la fonction définie par $x\,\mapsto \,\frac{1}{\sqrt{x+2}}$

1) Déterminer Df, l’ensemble de définition de f.

2) Déterminer les images de –1, 7 et –4.

3) Déterminer graphiquement le ou les antécédents de 2.

4) Déterminer par le calcul le ou les antécédents de –1.

5) Représenter graphiquement f.

Exercice 15 :

Soit la fonction f définie par $x\,\mapsto \,\frac{2}{x-\pi}$

1) Déterminer l’ensemble de définition de f.

2) Déterminer les images de 0 et 2 $\pi$ .

3) Déterminer le ou les antécédents de 2 et 0.

4) Déterminer le signe de f.

5) Tracer la représentation graphique de f.

Exercice 16 :

On définit la fonction f sur ℝ par $x\,\mapsto \,\sqrt{2}x-\sqrt{3}$

1) Calculer l’image de $-\sqrt{2}$ .

2) Déterminer le ou les antécédents de 0 et $\sqrt{2}$ .

3) Étudier le signe de f.

4) Tracer la courbe Cf.

Exercice 17 :

Soit f la fonction définie sur $\mathbb{R}$ par :

1) Déterminer le signe de f.

2) f admet-elle un extrémum ?

3) Représenter graphiquement f.

Exercice 18 :

Soit f la fonction définie sur ]–3 ; +∞[ par $x\,\mapsto \,\frac{-1}{x+3}$

1) Étudier le signe de f.

2) Étudier les variations de f.

3) Tracer la courbe Cf.

Exercice 19 :

f est la fonction définie sur ℝ par

1) Déterminer le ou les antécédents de –1, –4 et 0

2) Déterminer le signe de f.

3) Montrer que f admet un extremum que l’on caractérisera.

4) Étudier les variations de f.

5) Représenter graphiquement f.

Exercice 20 :

Soit f la fonction définie par $x\,\mapsto \,\frac{x+4}{x+2}$

1) Déterminer Df.

2) Calculer les images de 0 et $\sqrt{2}$ .

3) Étudier les variations de f.

4) Représenter graphiquement f.

5) Résoudre graphiquement : f (x) = 3.

6) Résoudre graphiquement : f (x) > x.

Voir Exercices 11 à 20...

Exercice 21 :

Soient f : $x\,\mapsto \,-x^2\,+x$ et g : $x\,\mapsto \,3x+1$ .

1) Étudier les variations de f. puis celles de g.

2) Représenter graphiquement ces deux fonctions

3) Déterminer la position relative de Cf et Cg.

Exercice 22 :

Déterminer le sens de variation des fonctions ci-dessous:

1) x $\mapsto$ (x + 1)² − 5 sur ]− $\infty$ ; −1]

2) x $\mapsto$ $\frac{(2x+1)^2}{4}$ sur ]− $\infty$ ; −1/2]

3) x $\mapsto$ $\frac{1}{2x^2+1}$ sur R⁻

4) x $\mapsto$ 2 + $\frac{3}{x-2}$ sur ]2 ; + $\infty$ [

5) x $\mapsto$ $\sqrt{\frac{1}{x^2+1}}$ sur R⁺

6) x $\mapsto$ (| x | + 1)² sur R⁻

7) x $\mapsto$ 3 + $\frac{2}{(x-1)^2}$ sur ]1 ; + $\infty$ [

8) x $\mapsto$ $\sqrt{\frac{1}{x+1}}$ sur ]−1 ; + $\infty$ [

9) x $\mapsto$ $\sqrt{\frac{1}{x}-1}$ sur ]0 ; 1]

10) x $\mapsto$ $\frac{1}{\,|\,1-x^2\,\,|}$ sur [0 ; 1[

Exercice 23 :

Décrire le sens de variation de la fonction définie par la courbe donnée.

Exercice 24 :

Décrire le sens de variation de la fonction dont voici le tableau de variation.

Exercice 25 :

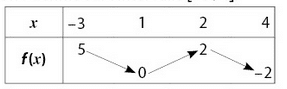
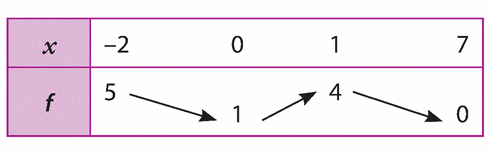
Le tableau ci-dessous donne le sens de variation d’une fonction f définie sur l’intervalle [-3;4].

Pour chaque affirmation, dire si elle est vraie ou fausse. Justifier votre réponse.

1.f est croissante sur [0;2].

2.f est décroissante sur [-1;1].

3.f(3)>f(2).

4. $f(0)\,\leq\,\,5$

5.Pour tout nombre réel x de l’intervalle [-3;2], $f(x)\,\geq\,\,0$ .

Exercice 26 :

f est une fonction définie sur l’intervalle [-3;6] telle que :

le maximum de f sur [-3;6] est égal à 5, il est atteint pour x=0.
le minimum de f sur [-3;6] est égal à -2, il est atteint pour x=3.
les antécédents de 0 par f sont atteints pour x=0;-3 et 6.
le maximum de f sur [-3;-1] est égal à 3 et il est atteint pour x= – 2.
f(-1)=2 et f est croissante sur [-1;0].

Tracer une courbe susceptible de représenter la fonction f dans ce repère.

Exercice 27 :

g est une fonction décroissante sur $\mathbb{R}$ telle que g(0)=1 et g(1)=0.

Quel est l’ensemble des nombres réels tels que :

a) $g(x)\geq\,\,0$

b) g(x)<1.

Exercice 28 :

Un QCM de mats en seconde (2de) sur les fonctions numériques.

Les questions 1. à 5. Comportent trois réponses possibles. Pour chacune de ces questions, une seule des réponses proposées est exacte. On demande de cocher cette réponse.

Une réponse inexacte enlève la moitié des points attribués à la question. L’absence de réponse à une question ne rapporte aucun point et n’en enlève aucun. Si le total est négatif, la note est ramenée à 0.

Soit f une fonction définie sur l’intervalle [-5;5] dont le tableau de variation est le suivant :(on suppose que la courbe représentative de f sur [-5;5] s’obtient « sans lever le crayon »)

Si on note la courbe représentative de la fonction f dans un repère, alors coupe l’axe des abscisses :	en un point en deux points en trois points
L’image de 0 est	égale à 0 négative inférieure à 2
Si , alors	et sont négatifs
Si $-1\leq\,\,x\leq\,\,5$ alors	$2\leq\,\,f(x)\leq\,\,3$ $-1\leq\,\,f(x)\leq\,\,5$ $1\leq\,\,f(x)\leq\,\,3$
Si x et y sont deux réels de l’intervalle (-1;3] tels que x est positif et y est négatif, alors	et sont de signes opposés

Exercice 29 :
Une joueuse de handball lance une balle devant elle.
Au bout de x mètres parcourus, la hauteur de la balle (en mètres) avant qu’elle ne touche
le sol est donnée par : .
Quelle est la hauteur de la balle après 20 mètres parcourus ?

Que peut-on en déduire pour la balle ?s
a) Montrer que .
b) Que peut-on dire du signe de ?
c) En déduire la hauteur maximale atteinte par la balle.

Exercice 30 :

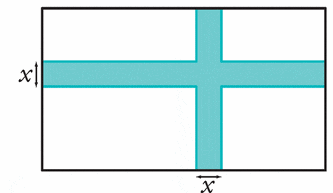
On considère un rectangle de longueur 7 et de largeur 5.
On trace à l’intérieur de celui-ci une croix de largeur x
variable comme indiqué ci-dessous.
On s’intéresse à l’aire de la croix bleue.
1. A quel intervalle x appartient-il ?
2. Exprimer l’aire A(x) de la croix bleue en fonction de x.
3. Avec la calculatrice, dresser le tableau de valeurs de avec un pas de 1.

Voir Exercices 21 à 30...

Exercice 31 :

Le prix de l’essence sans plomb est de 1 euro le litre.

Marius veut faire le plein de sa voiture. II compte mettre x litres dans
son réservoir vide qui peut contenir 40 litres.
La station dans laquelle il se sert ne délivre pas moins de 5 litres.
On considère la fonction P qui à chaque valeur de x associe
le prix payé par Marius.
1. D’après le contexte de l’exercice, à quel intervalle x appartient-il ?
2. Quel est l’ensemble de définition de la fonction P ?
3. Déterminer l’expression algébrique de la fonction P.

Exercice 32 :
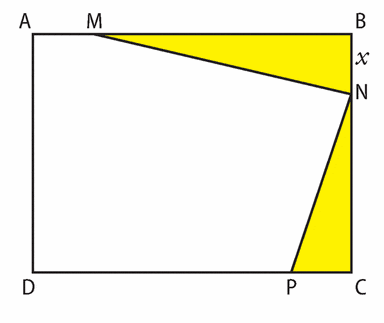
ABCD est un rectangle tel que AB 10 cm et BC = 8 cm.
N est un point mobile sur le segment [BC].
On note x la longueur en centimètres M et P sont les points respectifs de [AB] et [CD] tels que
AM = BN = CP = x.
Le but de cet exercice est de déterminer où placer N sur le segment [BC] pour que l’aire de la surface jaune, la somme des aires des triangles BMN et CNP, soit maximale.

1. Justifier que $x \in [O ; 8]$ .
2. Exprimer BM en fonction de x.
3. Exprimer CN en fonction de x.
4. Montrer que l’aire du triangle BMN est égale à
5. On note f la fonction qui à la longueur x associe l’aire totale de la surface jaune.
Vérifier que l’on a .

6.a) Montrer que .
b) En déduire la solution au problème posé.

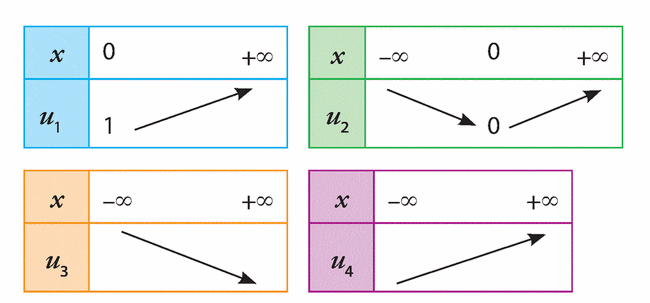
Exercice 33 :
Associer chaque fonction son tableau de variations
parmi les suivants.
a) f définie sur $\mathbb{R}$ par f(x) = —2x+ 4.
b) g définie sur $\mathbb{R}$ par g(x) = x^3 .
c) h définie sur $\mathbb{R}$ par h(x) = x^2 .
d) k définie sur $\mathbb{R}$ par k(x) = $\sqrt{x}+1$ .

Exercice 34 :
Une fonction f possède les propriétés suivantes :
• elle est définie sur [—3 ; 5] ;
• elle est croissante sur [—3 ; —I] ;
• elle est décroissante sur [—1 ; 4] ;
• elle est croissante sur [4 ; 5] ;
• sur l’intervalle [—3 ; 4], son maximum vaut 6 ;
• sur l’intervalle [-1 ; 5], son minimum vaut -3 ;
• l’image de —3 est I ;
• 5 est un antécédent de 7.
Dresser le tableau de variations de cette fonction.
Exercice 35 :

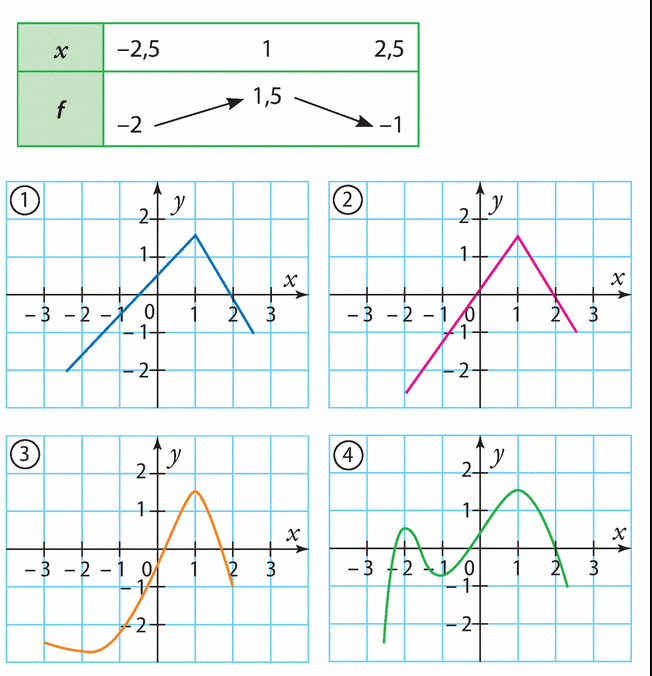
Voici le tableau de variations d’une fonction f.
Choisir la courbe correspondant ce tableau.

Exercice 36 :
Voici le tableau de variations d’une fonction f.
Comparer si possible les nombres suivants en justifiant.
1. a) f(2) et f(4).

b) f(- 2) et f(- 1).
2. Résoudre $f(x)\geq\, 0$ .
3. On sait de plus que .
Résoudre $f(x) \leq\, 4$ et .

Exercice 37 :
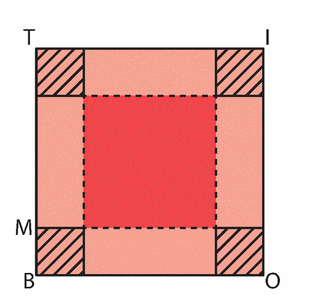
On considère un carré de côté 15 cm.

Dans chaque coin, on découpe un même carré pour obtenir un patron d’une boite sans couvercle.

A. Un cas particulier
1. Construire le patron d’une boite en choisissant BM = 3 cm.
2.Calculer son volume.
3. Peut-on réaliser une boîte sachant que BM = 8 cm ?
Expliquer.

B. Une fonction
On pose BM= x et on appelle V la fonction qui à x associe le volume de la boite sans couvercle.
1. Déterminer une expression de la fonction V.
2. Quel est l’ensemble de définition de V ?
3. A l’aide d’une calculatrice, ou d’un logiciel, tracer la courbe représentative de la fonction V.
4. Pour quelles valeurs de x le volume est-il supérieur ou égal 100 cm^3 ?
5. Le volume de cette boite peut-il dépasser 1 dL ?
Si oui, donner les dimensions d’une boite vérifiant cette condition.

Si non, expliquer pourquoi.

Exercice 38 :
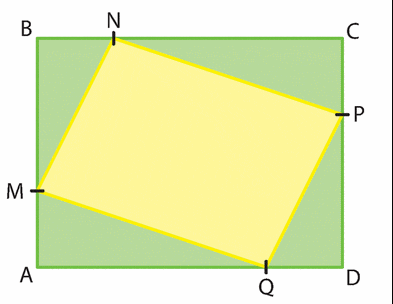
On considère un rectangle ABCD de dimensions AB = 6 cm et BC = 8 cm.
Sur le côté [AB], on place un point M quelconque.

On considère ensuite les points N sur [BC], P sur [CD] et Q sur [DA] tels que
AM = BN = CP = DQ.
On pose AM = x. On appelle f la fonction qui x associe la valeur de l’aire de MNPQ.
1. AM peut-elle prendre la valeur 7 ?
Quel est l’ensemble de définition de f?
2. Démontrer que .
3. A l’aide d’une calculatrice ou d’un logiciel, tracer la courbe
Représentative de f. Ajuster la fenêtre d’affichage.
4.Pour quelle(s) valeur(s) de x l’aire de MNPQ est-elle supérieure ou égale à 24 cm² ?

Exercice 39 :
g est une fonction dont on connait le tableau de variations.
a) Donner le sens de variation de la fonction g sur l’intervalle [2 ; 5].
b) En déduire quel est le nombre le plus grand entre g (3) et g(4).
2. Sur le modèle de la question précédente, comparer g (1) et g(l ,5).
3. Même question pour g (—2) et g (O).

Exercice 40 :
Recopier et compléter le tableau de variations proposé à partir de la représentation graphique suivante.

Voir Exercices 31 à 40...

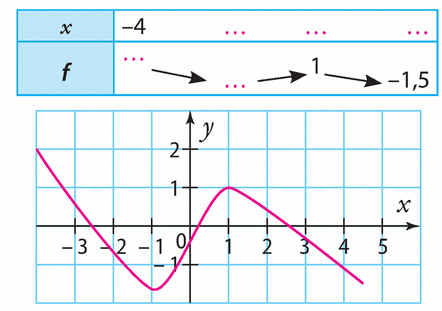
Exercice 41 :
Recopier et compléter le tableau de variations proposé à partir de la représentation graphique suivante :

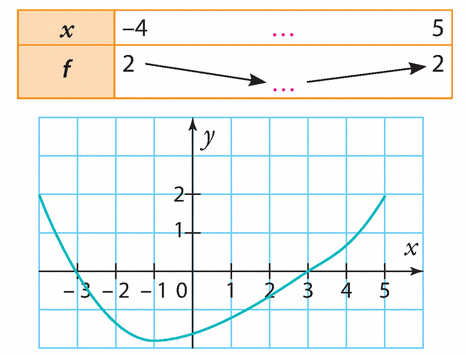
Exercice 42 :
Recopier et compléter le tableau de variations proposé partir de Ia représentation graphique suivante.

Exercice 43 :
Déterminer a et b pour que le tableau ci-dessous soit un tableau de valeurs d’une fonction h définie par
sur $\mathbb{R}$ .
2. La fonction h est-elle paire ? impaire ?
3. Déterminer les antécédents de —7 par h.

Exercice 44 :
On considère la fonction f définie sur $\mathbb{R}$ par f(x) = —2x+ 5.
1. Déterminer le ou les antécédents de —2 par f.
2. Écrire un algorithme ou un programme qui :
— demande une valeur b l’utilisateur ;
— calcule puis affiche le ou les antécédents de b par la
fonction f.

Exercice 45 :
1. A l’aide de la calculatrice, recopier et compléter le tableau de valeurs de la fonction h définie
sur [—2 ; 2] par h(x)=(3x+1)(5-x).
2. Déterminer tous les antécédents de 0 par h.

Voir Exercices 41 à 45...

Télécharger puis imprimer cette fiche en PDF.

Télécharger ou imprimer cette fiche «les fonctions et lecture graphique : exercices de maths en 2de corrigés en PDF.» au format PDF afin de pouvoir travailler en totale autonomie.

Vous devez vous inscrire ou vous connecter à votre compte afin de pouvoir télécharger ce document au format PDF.

Réviser les cours et exercices avec nos Q.C.M :

Q.C.M en 6ème Q.C.M en 5ème Q.C.M en 4ème Q.C.M en 3ème Q.C.M en 2de Q.C.M en 1ère Q.C.M en Terminale

D'autres ressources pour progresser en autonomie :

Chronomètre Horloge France Tables Multiplication Arrondir des décimaux Rapporteur et Angles Médiatrice Symétrie Axiale d'un triangle Symétrie Centrale d'un triangle Translation d'un triangle Rotation Homothétie Bissectrice Tracer droite parallèle Conversion Aires et Volumes Addition de deux relatifs Soustraction Relatifs Addition et soustraction de trois relatifs Produit Deux Relatifs Produit Trois Relatifs Quotient Relatifs Carré Entier Racine Carrée Théorème Pythagore Liste Diviseurs Décomposition Facteurs Premiers Calcul du PGCD PGCD Algorithme Euclide Test Nombre Premier Déterminer Fonction Linéaire Déterminer Fonction Affine Traceur Courbe Trigonométrie Angle Trigonométrie Longueur Périmètre d'un Cercle Aire d'un Disque Volume du Parallélépipède Rectangle Volume du cylindre Surface d'une Sphère et Volume d'une boule Volume d'une pyramide à base rectangulaire Section d'une pyramide Visualiser Section Cône en 2D Section d'un Cône Carte Mondiale Coordonnées Géographiques

Mathématiques Web c'est 2 250 275 fiches de cours et d'exercices téléchargées.