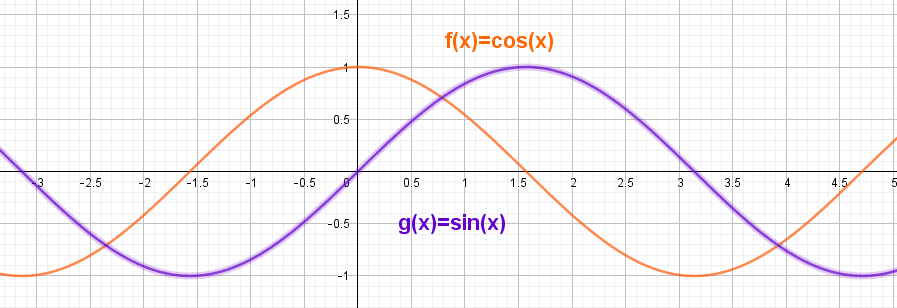Trigonométrie et relations métriques : cours en 1ère en PDF.

sommaire

1 I. Les fonctions de la trigonométrie
2 II. Cosinus et sinus d’angles remarquables en trigonométrie.
3 III.Visualisation des sinus et cosinus sur le cercle trigonométrique.
4 IV.Formules usuelles concernant les angles associés.
5 V.Représentations graphiques des fonctions sinus et cosinus

La trigonométrie avec un cours de maths en 1ère reposant aussi sur les relations métriques dans un triangle quelconque. Parmi celles-ci, vous avez les relations d’Al-Kashi, théorème de Pythagore généralisé. Cette leçon est à télécharger gratuitement au format PDF.

I. Les fonctions de la trigonométrie

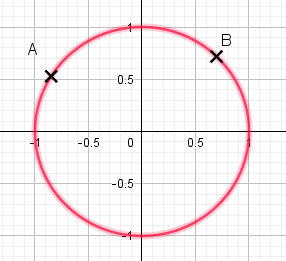
Dans cette leçon, $(O,\vec{u},\vec{v})$ est un repère orthonormal de sens direct.

Les points A et B sont donc sur le cercle trigonométrique de centre O et de rayon 1.

1.Définition du sinus et du cosinus d’un nombre réel.

Définition :

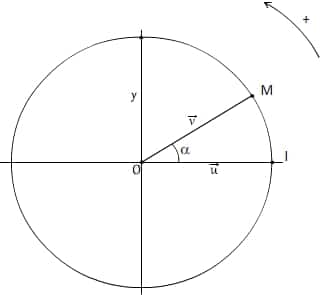
A tout réel $\alpha$ , on associe le point M du cercle trigonométrique tel que l’angle orienté $(\vec{u},\vec{OM})$ mesure $\alpha$ radian(s).

Le cosinus et le sinus de $\alpha$ sont donc les coordonnées de M dans le repère $(O,\vec{u},\vec{v})$ .

On a: $M(cos\alpha\,,sin\,\alpha\,)$ c’est à dire : $\vec{OM}=cos\alpha\,\vec{u}+sin\alpha\,\vec{\,v}$ .

2.Premières propriétés en trigonométrie .

Propriétés :

Si $\alpha$ =0 alors le point du cercle trigonométrique associé à $\alpha$ est le point A(1 ; 0). Donc cos(0) = 1 et sin(0) = 0

Si $\alpha\,=\frac{\pi}{2}$ , alors le point du cercle trigonométrique associé à $\alpha$ est B(0 ; 1).Donc $cos(\frac{\pi}{2})=0$ et $sin(\frac{\pi}{2})=1$ .

Si $\alpha\,=\pi$ , alors x est associé à A'(-1 ;0). Donc $cos(\,\pi\,)=-1$ et $sin(\,\pi\,)=0$ .

Si $\alpha\,=-\frac{\pi}{2}$ alors $\alpha$ est associé à B'(0 ;-1). Donc $cos(-\frac{\pi}{2})=0$ et $sin(-\frac{\pi}{2})=-1$ .

Si $\alpha$ est un réel alors pour tout entier relatif k, les réels $\alpha$ et $\alpha\,+2k\pi$ sont associés au même point M.
En effet ce sont deux mesures de l’angle orienté .
Donc, pour tout nombre réel x et tout entier relatif k, on a:

$cos(\,\alpha\,+2k\pi)\,=\,cox(\,\alpha\,)$

$sin(\,\alpha\,+2k\pi)\,=\,sin(\,\alpha\,)$

On dit que les fonctions cosinus et sinus sont périodiques de période $2\pi$ , car T = $2\pi$ est le plus petit réel strictement positif tel que: cos ( $\alpha$ + T) = cos $\alpha$ et sin ( $\alpha$ + T) = sin $\alpha$ .

Le théorème de Pythagore permet de prouver l’égalité:
$(sin\,\alpha\,)^2\,+\,(cos\,\alpha)^2\,=\,1$ que l’on écrit aussi sous la forme: $sin^2\,\alpha\,+\,cos^2\,\alpha\,=\,1$ .

3.Signe du sinus et du cosinus.

Par définition, le sinus et le cosinus de tout nombre réel appartiennent à l’intervalle [-1 ; 1].

Plus précisément, la position de M nous permet d’en savoir plus sur le cosinus et le sinus de $\alpha$ .

Propriétés :

On a :

Si $\alpha\,\in[0+2k\pi,\pi+\,2k\pi]$ alors $sin\alpha\,\geq\,\,0$ .
Si $\alpha\,\in[-\frac{\pi}{2}+2k\pi,\frac{\pi}{2}+\,2k\pi]$ alors $cos\alpha\,\geq\,\,0$ .

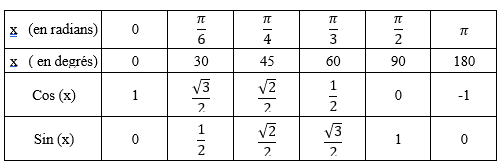
II. Cosinus et sinus d’angles remarquables en trigonométrie.

Tous ces résultats à connaître parfaitement sont résumés dans le tableau ci-dessous:

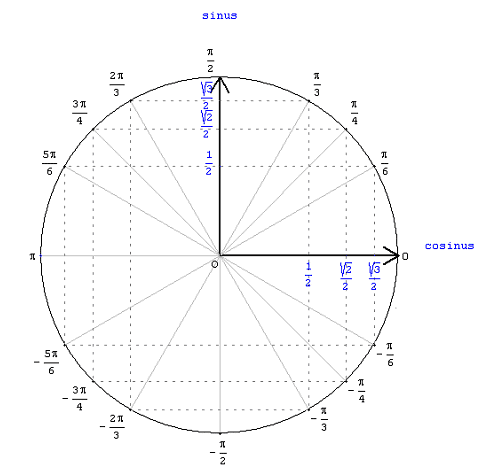
III.Visualisation des sinus et cosinus sur le cercle trigonométrique.

C’est un outil indispensable, qu’il est utile de bien visualiser afin d’être capable de retrouver rapidement les valeurs indiquées ci-dessous.

IV.Formules usuelles concernant les angles associés.

Propriétés :

Pour tout réel x, on a:

cos(–x) = cos(x) et sin(–x) = –sin(x).

La fonction cosinus est donc paire et la fonction sinus est impaire.

Propriétés :

Pour tout réel x, on a:

cos( $\pi$ – x) = – cos(x) et sin( $\pi$ – x) = sin(x).

Propriétés :

Pour tout réel x, on a:

cos( $\pi$ + x) = – cos(x) et sin( $\pi$ + x) = – sin(x).

Propriétés :

Pour tout réel x, on a:

cos( $\frac{\pi}{2}+x$ ) = – sin(x) et sin( $\frac{\pi}{2}+x$ ) = cos(x).

Propriétés :

Pour tout réel x, on a:

cos( $\frac{\pi}{2}-x$ ) = sin(x) et sin( $\frac{\pi}{2}-x$ ) = cos(x).

V.Représentations graphiques des fonctions sinus et cosinus

Télécharger puis imprimer cette fiche en PDF.

Télécharger ou imprimer cette fiche «trigonométrie et relations métriques : cours de maths en 1ère en PDF.» au format PDF afin de pouvoir travailler en totale autonomie.

Vous devez vous inscrire ou vous connecter à votre compte afin de pouvoir télécharger ce document au format PDF.

Réviser les cours et exercices avec nos Q.C.M :

Q.C.M en 6ème Q.C.M en 5ème Q.C.M en 4ème Q.C.M en 3ème Q.C.M en 2de Q.C.M en 1ère Q.C.M en Terminale

D'autres ressources pour progresser en autonomie :

Chronomètre Horloge France Tables Multiplication Arrondir des décimaux Rapporteur et Angles Médiatrice Symétrie Axiale d'un triangle Symétrie Centrale d'un triangle Translation d'un triangle Rotation Homothétie Bissectrice Tracer droite parallèle Conversion Aires et Volumes Addition de deux relatifs Soustraction Relatifs Addition et soustraction de trois relatifs Produit Deux Relatifs Produit Trois Relatifs Quotient Relatifs Carré Entier Racine Carrée Théorème Pythagore Liste Diviseurs Décomposition Facteurs Premiers Calcul du PGCD PGCD Algorithme Euclide Test Nombre Premier Déterminer Fonction Linéaire Déterminer Fonction Affine Traceur Courbe Trigonométrie Angle Trigonométrie Longueur Périmètre d'un Cercle Aire d'un Disque Volume du Parallélépipède Rectangle Volume du cylindre Surface d'une Sphère et Volume d'une boule Volume d'une pyramide à base rectangulaire Section d'une pyramide Visualiser Section Cône en 2D Section d'un Cône Carte Mondiale Coordonnées Géographiques

Mathématiques Web c'est 2 253 866 fiches de cours et d'exercices téléchargées.