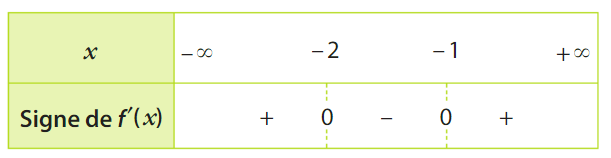Fonctions : exercices de maths en 1ère corrigés en PDF.

Les fonctions numériques à travers des exercices de maths en 1ère corrigés afin de vous exercez en ligne. L’élève de vra être capable de déterminer l’ensemble de définition et d’étudier la fonction en déterminant son sens de variation à l’aide de l’étude de la dérivée ou avec des tableaux de signes ou des tableaux de variation. L’étude de la tangente en un point d’une courbe et la corrélation avec le nombre dérivée.Vous retrouverez les notions suivantes :

domaine de définition d’une fonction;
limite d’une fonction;
asymptote à une courbe;
forme canonique;
parité d’une fonction;
sens de variations d’une fonctions.

Ces énoncés sont accompagnés de leur correction afin de vous auto-corriger et relever vos erreurs Cette fiche en première est à consulter en ligne ou à télécharger au format PDF.

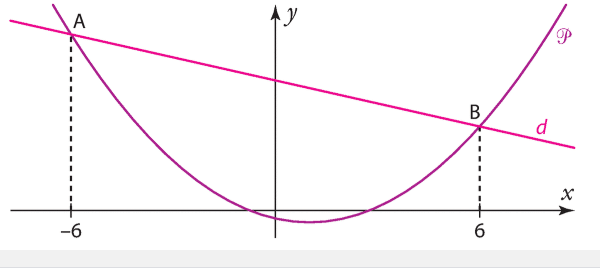
Exercice 1 :

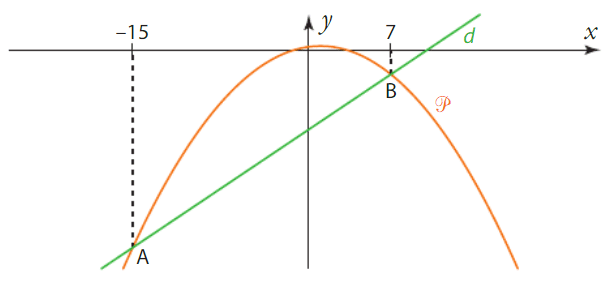
1)Recopier et compléter les phrases suivantes.

a) » La parabole et la droite d se coupent en … ».

b) » La parabole est située strictement au-dessus de la droite d sur … ».

« La parabole est située strictement en-dessous de la droite d sur … ».

2)En déduire les solutions des équations et inéquations.

a) f(x) = g(x). b) f(x)>g(x). c) f(x) < g(x).

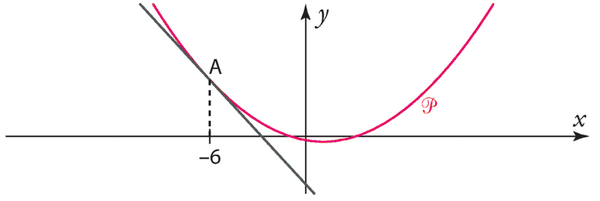
Exercice 2 :

1)Etudier la position relative de la parabole et de la droite .

2)En déduire les solutions des équations et des inéquations suivantes :

a) f(x) = g(x). b) f(x)>g(x). c) f(x) < g(x).

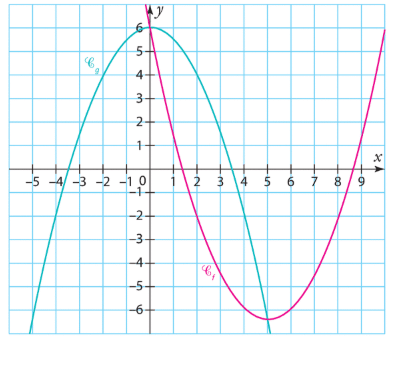
Exercice 3 :

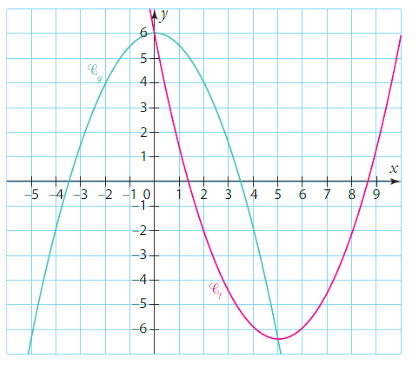
Soient f et g deux fonctions définies sur $\mathbb{R}$ dont les courbes et sont représentées

ci-dessous dans un repère du plan.

1)Etudier la position relative des courbes et .

2) En déduire les solutions des équations et inéquations suivantes.

a) f(x) = g(x). b) f(x)>g(x). c) f(x) < g(x).

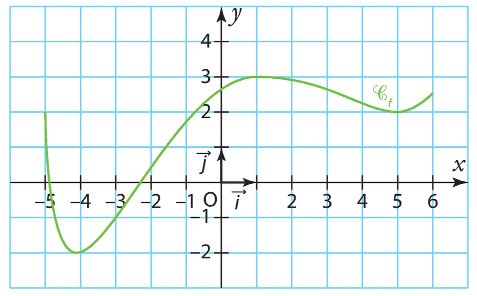
Exercice 4 :

Soit f une fonction définie et dérivable sur l’intervalle [- 5 ; 6 ].

La courbe représentative de f est tracée ci-dessous dans un repère du plan.

1)Décrire les variations de f sur [- 5 ; 6].

2) En déduire le tableau de signes de la fonction dérivée f ‘ sur [- 5 ; 6 ].

Exercice 5 :

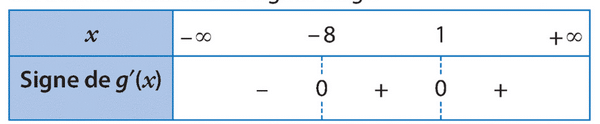
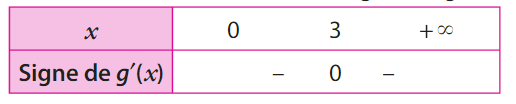
Soit g une fonction dérivable sur $]0;+\infty[$ et g ‘ sa dérivée.

On donne le tableau de signes de g ‘.

La fonction g admet-elle un extremum local ?

Si oui, est-ce un maximum ?

Exercice 6 :

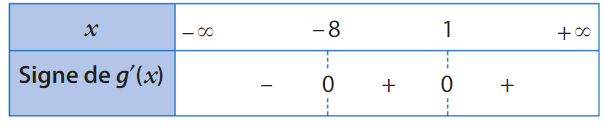
Soit g une fonction dérivable sur $\mathbb{R}$ et g ‘ sa dérivée.

On donne le tableau de signes de g ‘.

1)La fonction g admet-elle un minimum local ?

Si oui, en quelle valeur ?

2)La fonction g admet-elle un maximum local ?

Si oui, en quelle valeur?

Exercice 7 :

Soit f la fonction définie sur $\mathbb{R}$ par $f(x)=\frac{3}{4}x^2-15x+100$ .

1)Justifier que f est dérivable sur $\mathbb{R}$ et calculer f ‘ (x) pour tout réel x.

2)Dresser le tableau de signes de f ‘ (x) sur $\mathbb{R}$ .

3)En déduire que f admet un extremum local en une valeur que l’on déterminera.

Exercice 8 :

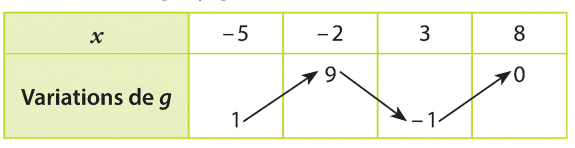
On a le tableau de variations d’une fonction g définie et dérivable sur [- 5 ; 8 ].

a)Donner un encadrement de g(x) lorsque $3\leq\, x\leq\, 8$ .

b)Donner un encadrement de g(x) lorsque $-2\leq\, x\leq\, 3$ .

c)Donner un encadrement de g(x) lorsque $-5\leq\, x\leq\, 3$ .

d) Soient a et b deux réels tels que $-5\leq\, a<b\leq\, -2$ .

e) Soient a et b deux réels tels que $-2\leq\, a<b\leq\, 3$ .

Comparer g(a) et g(b).

f) Soit $a\in[-5;-2]$ et $b\in[3;8]$ . Comparer g(a) et g(b).

Exercice 9 :

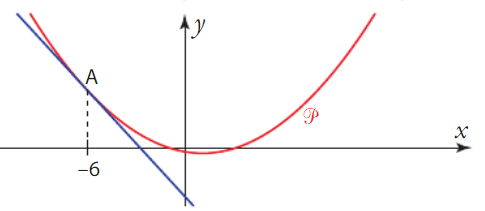
1. Etudier la position relative de la parabole et de la droite d.
2. En déduire les solutions des équations et inéquations.
a) f(x) = g(x)
b) f(x) > g(x)
c) f(x) < g(x)

Exercice 10 :

1.Étudier la position relative de la parabole et de la droite d.
2.En déduire les solutions des équations et inéquations suivantes :
a) f(x) = g(x)
b) f(x) > g(x)
c) f(x) < g(x)

Exercice 11 :

Soient f et g deux fonctions définies sur $\mathbb{R}$ dont les courbes et sont représentées ci-dessous dans un repère du plan.
1 . Étudier la position relative des courbes et .
2. En déduire les solutions des équations et inéquations suivantes.
a) f(x) = g(x)
b) f(x) > g(x)
c) f(x)< g(x)

Exercice 12 :

Soit f et g deux fonctions définies sur $\mathbb{R}$ par et .
1. Montrer, que pour tout réel x, .
2. Étudier, selon les valeurs de x, le signe de f(x) — g(x).
3. En déduire la position relative des courbes et .

Exercice 13 :

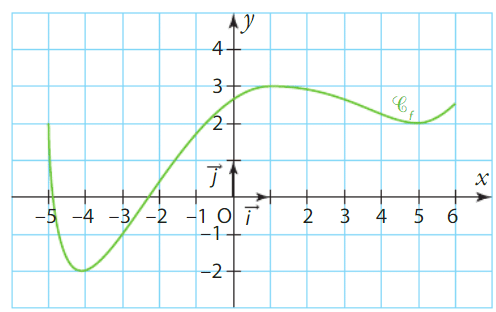
Soit f une fonction définie et dérivable sur l’intervalle [- 5 ; 6].

La courbe représentative de f est tracée ci-dessous dans un repère du plan.

1.Décrire les variations de f sur [- 5 ; 6].
2.En déduire le tableau de signes de la fonction dérivée sur [-5 ; 6].

Exercice 14 :

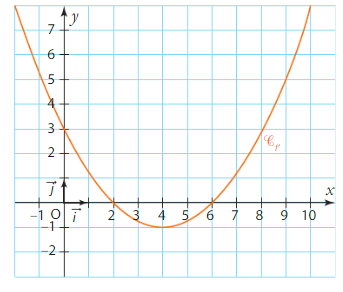
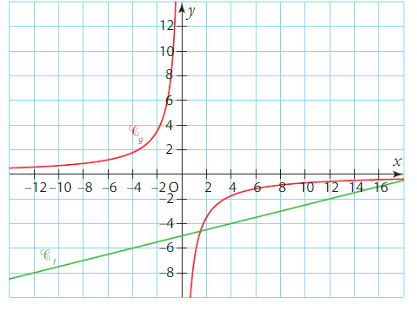
Soit f une fonction définie et dérivable sur l’intervalle [- 2 ; 10].

Sa dérivée est la fonction représentée par la courbe ci-dessous dans un repère du plan.
1 . Lire graphiquement le signe de selon les valeurs de x de l’intervalle [ – 2 ; 10].

Et présenter vos résultats dans un tableau de signes.
2. En déduire le tableau de variations de la fonction f sur l’intervalle [ – 2 ; 10].

Exercice 15 :

Soit f une fonction dérivable sur $\mathbb{R}$ et sa dérivée. On donne le tableau de signes de .

La fonction f admet-elle un extremum local ? Si oui, est-ce un maximum ou un minimum ?

Exercice 16 :

Soit g une fonction dérivable sur $]0;+\infty[$ et sa dérivée.

On donne le tableau de signes de .

La fonction g admet-elle un extremum local ? Si oui, est-ce un maximum ou un minimum ?

Exercice 17 :

Soit f une fonction dérivable sur $\mathbb{R}$ et sa dérivée.

On donne le tableau de signes de .
1. La fonction f admet-elle un minimum local ? Si oui, en quelle valeur ?
2. La fonction f admet-elle un maximum local ? Si oui, en quelle valeur ?

Exercice 18 :

Soit g une fonction dérivable sur $\mathbb{R}$ et sa dérivée.
On donne le tableau de signes de .

1. La fonction g admet-elle un minimum local ? Si oui, en quelle valeur ?
La fonction g admet-elle un maximum local ? Si oui, en quelle valeur ?

Exercice 19 :

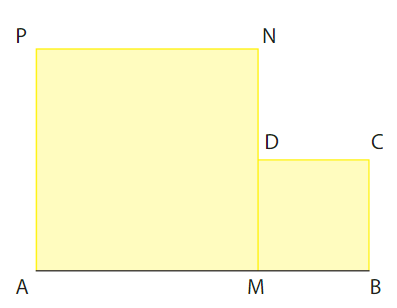
Soit un segment [AB] de longueur 10 et M un point de ce segment.
Du même côté de ce segment, on construit deux carrés AMNP et MBCD.

On pose AM = x et on étudie l’aire du domaine formé par ces deux carrés en fonction de x.

1.A quel intervalle I appartient le réel x ?
2. Soit f(x) l’aire du domaine.
Montrer que, pour tout réel x de l, on a:

3. Justifier que la fonction f est dérivable sur I et déterminer pour tout x de I.
4. En déduire les variations de f sur I et la valeur de x pour laquelle l’aire du domaine est minimale.

Exercice 20 :

Soit f une fonction définie sur $\mathbb{R}$ par $f(x)=\frac{1}{4}x-5$ et g une fonction définie sur $\mathbb{R}^*$ par $g(x)= -\frac{7}{x}$ .
a) Montrer que, pour tout réel x non nul :
$f(x)-g(x)=\frac{\frac{1}{4}x^2-5x+7}{x}$ .
b) Étudier, selon les valeurs de x, le signe de f(x) — g(x).
c) En déduire la position relative des courbes et .

Exercice 21 :

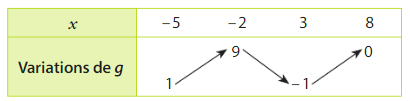
On a le tableau de variations d’une fonction g définie et dérivable sur [ – 5 ; 8] :

a) Donner un encadrement de lorsque $3 \leq\, x\leq\, 8$ .
b) Donner un encadrement de lorsque $-2\leq\, x\leq\, 3$ .
c) Donner un encadrement de lorsque $-5\leq\, x\leq\, 3$ .
d) Soient a et b deux réels tels que $-5 \leq\, a < b\leq\, -2.$
Comparer g(a) et g(b).
e) Soient a et b deux réels tels que $-2 \leq\, a < b\leq\, 3.$

Comparer g(a) et g(b).
f) Soit $a \in [-5 ;-2]$ et $b \in [3 ;8]$ .

Comparer g(a) et g(b).

Télécharger puis imprimer cette fiche en PDF.

Télécharger ou imprimer cette fiche «fonctions : exercices de maths en 1ère corrigés en PDF.» au format PDF afin de pouvoir travailler en totale autonomie.

Vous devez vous inscrire ou vous connecter à votre compte afin de pouvoir télécharger ce document au format PDF.

D'autres cours et exercices à consulter

Mathématiques Web c'est 2 268 671 fiches de cours et d'exercices téléchargées.