Trigonométrie : exercices en 1ère de maths corrigés en PDF.

La trigonométrie avec des exercices de maths en 1ère corrigés afin de vous permettre de réviser en ligne. De plus, ce chapitre permet de développer des compétences nouvelles. La trigonométrie en 1ère vous permet de progresser tout au long de l’année scolaire.

Cette fiche fait intervenir les notions suivantes :

formule d’addition;
formules de trigonométrie;
cercle trigonométrique;
formules d’Al-Kashi;
formule de Pythagore généralisée;
mesure principale d’un angle.

Ces énoncés sont accompagnés de leur correction et ils vous permettront de combler vos lacunes afin de progresser en première.

Exercice 1 :

Soit g la fonction définie sur $\mathbb{R}$ par :

1)Montrer que g est paire. Interpréter graphiquement.

2)Montrer que g est $\frac{\pi}{2}$ – périodique.

Exercice 2 :

soit g la fonction définie sur $\mathbb{R}$ par :

1)Montrer que g n’est ni paire ni impaire.

2)Montrer que g est $2\pi$ – périodique. Interpréter graphiquement.

3)Montrer que, pour tout réel , $-2\leq\, g(x)\leq\, 2$ .

Exercice 3 :

1)A partir de $cos(\frac{\pi}{3})$ , déterminer $cos(-\frac{\pi}{3})$ puis $cos(\frac{2\pi}{3})$ .

2)Même question avec $sin(-\frac{\pi}{3})$ puis $sin(\frac{2\pi}{3})$ .

Exercice 4 :

1)Résoudre sur $[0;2\pi[$ l’équation $cos(x)=\frac{\sqrt{3}}{2}$ .

2)Résoudre sur $[0;2\pi[$ , l’équation $sin(x)=\frac{\sqrt{2}}{2}$ .

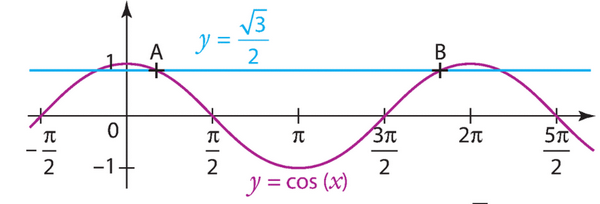
Exercice 5 :

1.Donner les abscisses des points A et B.

2)Résoudre sur $[0;2\pi[$ , l’équation $cos(x)=\frac{\sqrt{3}}{2}$ .

3)Résoudre sur $[0;2\pi[$ , l’inéquation $cos(x) \leq\, \frac{\sqrt{3}}{2}$ .

Exercice 6 :

Dans chaque cas, vérifier que la fonction f est T-périodique.

$a)f:x \mapsto cos(2\pi x)$ et T = 1.

$b)f:x \mapsto sin(3x)$ et $T=\frac{2\pi}{3}$ .

$c)f:x \mapsto \frac{2}{3}cos(7x+\frac{\pi}{4})$ et $T=\frac{2\pi}{7}$ .

$d)f:x \mapsto \frac{10}{7}sin(\frac{5x-8}{3})$ et $T=\frac{6\pi}{5}$ .

Exercice 7 :

1.a)Déterminer un réel x appartenant à l’intervalle $]-\pi;\pi[$ associé à $\frac{91\pi}{4}$ .

b)En déduire $cos(\frac{91\pi}{4})$ puis, $sin(\frac{91\pi}{4})$ .

2.a)Calculer $cos(-\frac{13\pi}{6})$ .

b)Calculer $sin(-\frac{81\pi}{2})$ .

3)a)Calculer $cos(\frac{25\pi}{3})$ et en déduire $sin(\frac{25\pi}{3})$ .

b)Calculer $sin(\frac{45\pi}{6})$ et en déduire $cos(\frac{45\pi}{6})$ .

Exercice 8 :

Soit f la fonction définie sur $]-\pi ; \pi ]$ par :

$f(x) = 4cos^2(x) + 2(\sqrt{2} - l)cos(x) -\sqrt{2}.$
Le but de l’exercice est de trouver les solutions de l’équation
f(x) = 0 et de l’inéquation f(x) > 0.
1. On pose X = cos(x).
a) Montrer que -1 <X< 1.
b) Montrer que résoudre l’équation f(x) = 0 revient à
résoudre l’équation $4X^2 + 2(\sqrt{2} - l)X -\sqrt{2}=0.$

c)Résoudre sur [- 1 ; 1], l’équation $4X^2 + 2(\sqrt{2} - l)X -\sqrt{2}=0.$
On notera et les solutions obtenues.
d) En déduire les solutions sur $]-\pi ; \pi ]$ de l’équation f(x) = 0.
2. On pose X = cos(x).
a) Résoudre sur [-1 ; 1] l’inéquation $4X^2 + 2(\sqrt{2} - l)X -\sqrt{2}>0.$

Exercice 9 :

1. Un disque microsillon tournant 33 tours et $\frac{1}{3}$ de tour par minute contient 6 chansons pour une durée
totale de 60 min. La durée de chaque chanson est la même.
Le Saphir situé l’extrémité du bras de lecture étant situé en N au début de la 1ère chanson, sur quel demi-axe se trouvera-t-il la fin de la chanson ?

2. Un disque microsillon tourne 16 tours et $\frac{2}{3}$ de tour par minute.

La durée de chaque chanson est égale 5 min.
Le saphir situé l’extrémité du bras de lecture étant situé en P au début de la 1ère chanson, sur quel demi-axe se trouvera-t-il :
a) au bout de 3 min ?
b) au bout de 4 min ?
c) à la fin de la 1ère chanson ?
d) à la fin de la 2ème chanson ?

Exercice 10 :

Soit f la fonction définie sur $\mathbb{R}$ par $f(x)=\frac{cos(x)}{3+sin^2(x)}$ .
1. Montrer que f est paire et $2\pi$ -périodique.

Interpréter graphiquement.
2. En déduire le plus petit intervalle I possible pour étudier f.
3. On admet que f est dérivable de dérivée :

$f'(x)=\frac{sin(x)(sin^2(x)-5)}{(3+sin^2(x))^2}$ .
a) En déduire les variations de la fonction f sur l.
b) Préciser les extrema locaux de f sur l.
c) Tracer la courbe représentative de f sur [- $\pi$ ; 3 $\pi$ ].

Exercice 12 :

Soit f la fonction définie sur $\mathbb{R}$ par $f (x) =-\frac{cos^3(x)}{3}$ .
1. Montrer que f est paire et $2\pi$ -périodique. Interpréter graphiquement.
2. On admet que la dérivée de la fonction f est la fonction définie par :
.

a) Étudier le signe de .
b) En déduire le sens de variation de la fonction f sur l’intervalle [0 ; $2\pi$ [.
c) Dresser le tableau de variations de la fonction f sur l’intervalle $[-\pi;3\pi[$ .

Exercice 13 :

On note (E) l’équation .
1.Montrer que les solutions de cette équation appartiennent l’intervalle [—1 ; 1].
2. Soit f la fonction définie sur l’intervalle [—1 ; 1] par f(x) = cos(x) + x.
a) Tracer f à l’aide de la calculatrice puis conjecturer le nombre de solutions de l’équation (E).
Justifier la démarche.
b) On admet que la dérivée de la fonction $x \mapsto cos(x)$ est la fonction $x \mapsto -sin(x)$ .

En déduire que .
c) Étudier le signe de et en déduire le sens de variation de la fonction f sur l’intervalle [—1 ; 1].
d) A l’aide de la calculatrice, donner une valeur approchée à 0,01 prés de la (ou les) solution(s).

Exercice 14 :

Les lentilles situées en haut de ce phare ont une portée lumineuse de 45 km et
une durée de rotation de 5 secondes.
1.Déterminer l’angle parcouru par une lentille en 1 seconde.
2. Calculer l’aire balayée par une lentille en 1 seconde.

Exercice 15 :

Soit m un paramètre réel non nul et la fonction définie sur $\mathbb{R}$ par .
1. Montrer que est paire. Interpréter graphiquement.
2. Montrer que est périodique de période $T=\frac{2\pi}{m}$ .
3. En déduire qu’on peut étudier sur l’intervalle $[0;\frac{\pi}{m}]$ .
4. On admet que est dérivable de dérivée :

. Selon m :
a) Déterminer le signe de sur l’intervalle $[0;\frac{\pi}{m}]$ .

b) En déduire les variations de sur l’intervalle $[0;\frac{\pi}{m}]$ .
c) Dresser le tableau de variations de sur l’intervalle $[0;\frac{\pi}{m}]$ puis sur l’intervalle $[-\frac{\pi}{m};\frac{2\pi}{m}]$ .

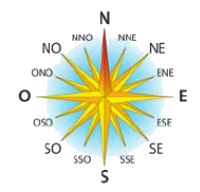
Exercice 16 :

On considère la rose des vents ci-dessous.
On admet qu’un réel ayant pour image le sens « E » est 0 et qu’un réel ayant le sens « N » est $\frac{\pi}{2}$ .

1.Déterminer un réel ayant pour image le sens « O ».
2.Déterminer un réel ayant pour image le sens « S ».
3.Déterminer un réel ayant pour image le sens « NE ».
4.a) Déterminer un réel ayant pour image le sens « NNE »
b) Par symétrie, quel réel peut avoir pour image le sens « SSE» ?
c) Par symétrie, quel réel peut avoir pour image le sens « NNO » ?

Exercice 17 :

Calculer :

$A=cos(\frac{\pi}{4})+cos(\frac{3\pi}{4})$

$B=sin(\frac{\pi}{3})-cos(\frac{\pi}{4})+sin(\frac{5\pi}{3})$

$C=cos^2(\frac{\pi}{2})-sin^2(\frac{\pi}{2})$

Exercice 18 :

Calculer :

$D=-cos(\frac{7\pi}{3})+cos(\frac{41\pi}{3})$

$B=sin(-\frac{87\pi}{4}) +sin(-\frac{21\pi}{6})$

Exercice 19 :

Exercice 20 :

Soit f la fonction définie sur $\mathbb{R}$ par .

La courbe représentative de f passe par les points $M(-\frac{\pi}{2};2)$ et $N(\frac{\pi}{4};\sqrt{2})$ .

1.A l’aide des points M et N, déterminer les réels a et b.
2.En déduire l’expression de f en fonction de x.
3. Montrer que f est $2\pi$ -périodique. Interpréter graphiquement.

4. f est-elle paire ? impaire ? Justifier.

4/5 - (50 votes)

Télécharger puis imprimer cette fiche en PDF.

Télécharger ou imprimer cette fiche «trigonométrie : exercices de maths en 1ère corrigés en PDF.» au format PDF afin de pouvoir travailler en totale autonomie.

D'autres cours et exercices à consulter

Mathématiques Web c'est 2 268 522 fiches de cours et d'exercices téléchargées.