Probabilités conditionnelles : exercices de maths corrigés en 1ère S

Les probabilités conditionnelles à travers des exercices de maths en 1ère corrigés qui font intervenir les notions suivantes :

D’abord les arbres pondérés, probabilités;
Ensuite, l’événement et probabilité conditionnelle;
Enfin, les pondérations et probabilités.

Ces énoncés vous permettent de vous entraîner sur de nombreuses ressources différentes afin d’être à l’aise sur le chapitre des probabilités et leur correction vous permettra de repérer vos erreur afin d’augmenter vos notes en première.

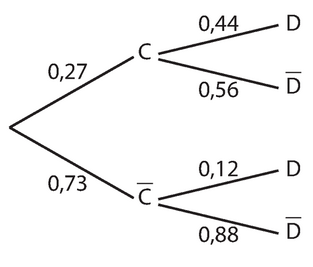
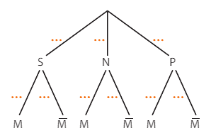
Exercice 1 :

Dans l’arbre ci- dessous, exprimer chacune des pondérations
comme une probabilité (par exemple $0,44\,=p_C(D)$ ).

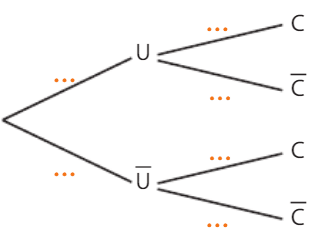
Exercice 2 :

Quand on lance un dé à 6 faces, on considère les événements :
A:« Le résultat est pair. »
B:«Le résultat est 2.»
C:«Le résultat est inférieur ou égal à 4.»
1. a) Décrire la probabilité par une phrase.

b) Même question pour $P_A(\overline{B})$ .

2. a) Ecrire la probabilité que le résultat soit pair sachant qu’il
est inférieur ou égal à 4 avec la notation des probabilités
conditionnelles.

b) Même question pour la probabilité que le résultat soit
inférieur ou égal à 4 sachant qu’il est pair.

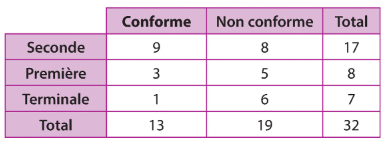
Exercice 3 :

Un professeur de mathématiques a trié sa bibliothèque dans laquelle figurent 32 manuels de différents niveaux,
certains étant conformes aux programmes actuels et d’autres, plus vieux, n’y étant pas conformes.

La répartition de ces manuels est donnée par le tableau ci-dessous :

Il prend un de ces manuels au hasard et on considère les événements :

C:« Le manuel est conforme aux programmes actuels. »
S :« Le manuel est un manuel de Seconde. »

T:« Le manuel est un manuel de Terminale. »

1. Calculer p(C), p(S) et p(T).

2. Calculer et .

3. Calculer $p_C(\overline{S})$ et $p_{\overline{S}}(C)$ .

Exercice 4 :

La répartition des poivrons chez un maraîcher est :

40 % de poivrons verts dont 60 % sont bio.
45 % de poivrons rouges dont 50 % sont bio.
15 % de poivrons jaunes dont 80 % sont bio.

Nino achète un de ces poivrons au hasard et on note:

V l’événement « Le poivron est vert ».
R l’événement « Le poivron est rouge ».
J l’événement « Le poivron est jaune ».
B l’événement « Le poivron est bio ».

1. Recopier et compléter l’arbre pondéré ci-dessous représentant la situation.

2. Calculer la probabilité qu’il achète un poivron jaune bio.
3. Calculer p(B) puis p( $\overline{B}$ ).

Exercice 5 :

Sophie a mis des dragées dans une boîte, les unes contiennent une amande, les autres pas :

+ 30 % des dragées contiennent une amande ;
+ 40 % des dragées avec amande sont bleues et les autres roses ;
+ 25 % des dragées sans amande sont roses et les autres bleues.

Sophie choisit au hasard une dragée dans la boîte et on considère les événements :

A:« La dragée choisie contient une amande. »

B:« La dragée choisie est bleue. »

1. Représenter la situation par un arbre pondéré.

2. Montrer que $p(A \cap B) = 0,12$ .

3. Calculer p(B) puis en déduire .

4. Calculer $p_{\overline{B}}(A)$ .

5. Sophie préfère les dragées contenant une amande.
Doit-elle plutôt choisir une dragée bleue ou rose ?

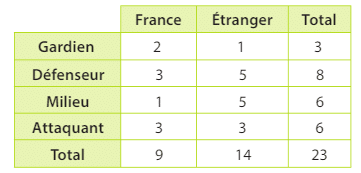
Exercice 6 :

On considère les 23 joueurs de football ayant gagné la coupe du monde 2018 selon leur poste et selon s’ils jouaient en France ou l’étranger durant cette saison 2017-2018:

On tire au hasard un joueur parmi les 23 et on considère les événements :
•G:« Le joueur est gardien. »
• D : « Le joueur est défenseur.
•M:« Le joueur est milieu. »
• A: « Le joueur est attaquant. »
•F : «Le joueur joue en France. »
1. Calculer p(G) et p(F).
2. Calculer , et .
3. Calculer $p_G(\overline{F})$ et $p_{\overline{F}}(D)$ .
4. Calculer .
5. Trouver une probabilité conditionnelle égale à $\frac{5}{8}$ .
6. Calculer $p_{G\cup\,D}(F)$ et $P_{\overline{F}}(M\,U\,A)$ .

Exercice 7 :

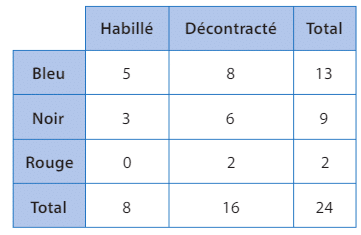
La répartition des pantalons de Gani est donnée par le tableau ci-dessous :

II prend un pantalon au hasard dans son armoire et on considère les événements :

B : «Le pantalon est bleu. »
N : «Le pantalon est noir. »
R : «Le pantalon est rouge. »
D : « Le pantalon est décontracté. »

Les événements suivants sont-ils indépendants ?
a) B et D
b) R et $\overline{D}$
c) N et D
d) N et $\overline{D}$

Exercice 8 :

Justin vérifie sa boite à lettres tous les soirs et la probabilité qu’il y ait du courrier est 0,47. On admet que la présence de courrier ou non dans sa boite lettres un soir n’a pas d’influence sur celle du soir
suivant.
Pourquoi peut-on penser que la répétition de cette épreuve deux soirs consécutifs est une succession
de deux épreuves indépendantes ?
2. Représenter cette succession de deux épreuves indépendantes par un arbre.
3. Représenter cette succession de deux épreuves indépendantes par un tableau double entrée.

Exercice 9 :

Ornella et Fanny Sont allées boire un verre et, au moment de partir, elles décident de
laisser un pourboire.
Pour cela, Ornella prend une pièce au hasard dans sa poche qui
contient deux pièces de 0,50 euro et une de 1 euro puis Fanny prend une pièce au hasard dans son porte-monnaie qui contient trois pièces de 0,20 euro, une de 1 euro et une de 2 euros.
1. Pourquoi peut-on penser que ces deux tirages sont une succession de deux épreuves indépendantes ?
2. Représenter cette succession de deux épreuves indépendantes par un arbre.

3.Représenter cette succession de deux épreuves indépendantes par un tableau double entrée.

Exercice 10 :

La production d’une entreprise de matériel mathématique est composée 70 % d’équerres et 30 % de
rapporteurs.
Suite un problème en usine, 20 % des équerres ont des défauts et 30 % des rapporteurs n’en ont pas.
Représenter la situation par un arbre pondéré après avoir énoncé les événements y apparaissant.

Exercice 11 :

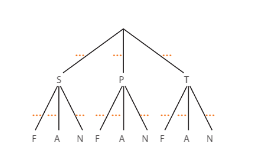
Dans l’association sportive d’un lycée. il y a :
• 24 % d’élèves de seconde dont 12 % font du football, 45 % de l’athlétisme et 43 % de la natation ;
•61 % d’élèves de première dont 34 % font du football. 44 % de l’athlétisme et 22 % de la natation :
• 15 % d’élèves de terminale dont 41 % font du football, 9 % de l’athlétisme et 50 % de la natation.
On prend un élève de l’association sportive et on considère les événements :
• S (resp. P. resp. T) : Cet élève est en Seconde (resp. première. resp. terminale).
• F (resp. A resp. N) : Cet élève pratique le football (resp. l’athlétisme, resp. la natation).
1. Recopier et compléter l’arbre pondéré ci-dessous représentant la situation.

2. a) Déterminer $p(N\cap\,S)$ .
b) Déterminer p(N) .
c) En déduire p_N(S) .
3. On considère un élève qui se rend à la piscine pour faire de la natation.
Est-il plus probable que ce soit un élève de seconde, première ou terminale ?
4. a) Déterminer $p(A\,\cup\,N)$ .
b) Déterminer la probabilité que l’élève soit en seconde ou qu’il fasse du football.

Exercice 12 :

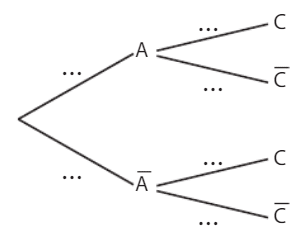
Le cuisinier d’une colonie de vacances a confectionné des beignets pour le goûter :
• 30 % des beignets sont à l’ananas, les autres sont aux pommes ;
• 35 % des beignets à l’ananas sont aromatisés à la cannelle, ainsi que 45 % des beignets aux pommes.

On choisit un beignet au hasard et on définit les événements A : « Le beignet
choisi est à l’ananas » et C: « Le beignet choisi est aromatisé à la cannelle ».
1. Reproduire et compléter l’arbre pondéré ci-dessous.
2. Les événements A et C sont-ils indépendants ? Justifier la réponse.

Exercice 13 :

Dans la chorale d’un lycée, il y 7 élèves de seconde, 9 élèves de première et n élèves de terminale.
De plus, parmi les élèves de seconde, il n’y a qu’une seule fille, contre 3 parmi les élèves de première et 6 parmi les élèves de terminale. On tire au sort un élève de la chorale.
Pour quelle(s) valeur(s) de n les événements « L’élève est en terminale » et « L’élève est une fille » sont-ils indépendants ?

Exercice 14 :

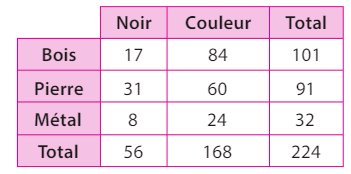
Annie a une collection d’éléphants miniatures dont la répartition est donnée ci-dessous.

Chaque semaine, elle tire au sort un éléphant pour le mettre sur son bureau au travail.
On considère les événements :
•N :« L’éléphant est noir. »
• B : « L’éléphant est en bois. »
• M :« L’éléphant est en métal. »
1. Calculer les probabilités suivantes.

a) p_B(N) b) $p_{\overline{N}}(B)$ c) $p_{B\cup\,M}(N)$

2. Les événements N et M sont-ils indépendants ?
3. Les événements N et B sont-ils indépendants ?

Exercice 15 :

Saumonix est poissonnier et 15 % du poisson qu’il vend a été péché par ses soins, 30 % vient d’un grossiste normand et le reste d’un grossiste de Paris.
II a remarqué que 5% de ses clients sont mécontents du poisson qu’il a lui-même péché, du poisson provenant du grossiste normand et 90 % du poisson de Paris.
un client achète un poisson Saumonix.
On considère les événements suivants
•S: » Le poisson a été péché par Saumonix. »
•N : »Le poisson provient du grossiste normand. »
P : » Le poisson prévient du grossiste de Paris. »
•M : « Le client est mécontent du poisson. »

1. Recopier et compléter l’arbre pondéré ci-dessous.

2. a) Calculer $p(P\cap\,M)$ et p(M).
b) Les événements S et M sont-ils indépendants ?
c) Un client est mécontent du poisson acheté.
Quelle est la probabilité que ce poisson ait été péché par Saumonix ?
3. Saumonix souhaite ramener le taux de mécontentement à 30 % en continuant à pécher 15 % de sa production.

Déterminer les proportions de poisson qu’il doit commander à cheque grossiste pour atteindre son objectif.

Exercice 16 :

Pour les prochaines vacances de Yannis, tout est presque réglé : ses parents lui ont assuré qu’il y a 90 % de chances que la famille parte Istanbul.
Par ailleurs, Yannis a constaté que pendant cette période de vacances, la probabilité qu’il ne pleuve pas s’il va Istanbul est 0,85.
Quelle est la probabilité qu’il parte Istanbul pour ses prochaines vacances et qu’il n’y pleuve pas ?

Exercice 17 :

Émilie a une entreprise de plomberie.
75 % de ses interventions sont programmées, le reste est « en urgence ».

Pour les interventions programmées, elle utilise son chalumeau 85 % du temps contre 90 % pour les interventions d’urgence.
Émilie part chez un client, on considère les événements :
• U: « L’intervention est en urgence. »
• C: « Émilie va devoir utiliser son chalumeau. »
1. Compléter l’arbre pondéré ci-dessous représentant la situation.
2. Calculer $p(U\,\cap\,C)$ et $p(\overline{U}\,\cap\,C)$ .
3. Déterminer la probabilité qu’Émilie doive utiliser son chalumeau pour cette intervention.

Exercice 18 :

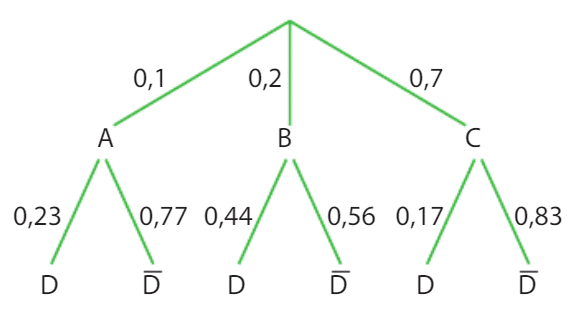
Pour des événements A, B, C et D tels que A, B et C forment une partition de l’univers, on considère la situation représentée par l’arbre pondéré ci-dessous :

1.Les événements A et D sont-ils indépendants ?
2.Les événements B et D sont-ils indépendants ?

Exercice 19 :

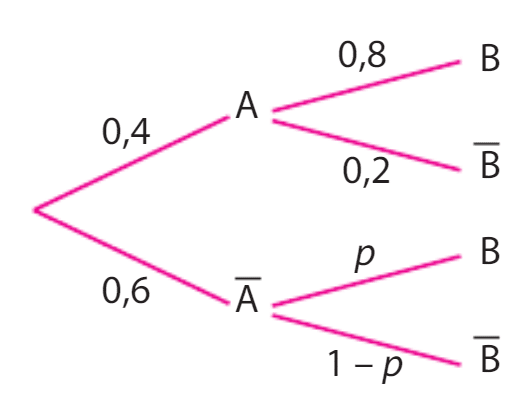
On considère deux événements A et B et l’arbre pondéré associé ci-dessous.
Déterminer p pour que les événements A et B soient indépendants.

Voir Exercices 11 à 19...

Télécharger puis imprimer cette fiche en PDF.

Télécharger ou imprimer cette fiche «probabilités conditionnelles : exercices de maths en 1ère corrigés en PDF.» au format PDF afin de pouvoir travailler en totale autonomie.

Réviser les cours et exercices avec nos Q.C.M :

Q.C.M en 6ème Q.C.M en 5ème Q.C.M en 4ème Q.C.M en 3ème Q.C.M en 2de Q.C.M en 1ère Q.C.M en Terminale

D'autres ressources pour progresser en autonomie :

Chronomètre Horloge France Tables Multiplication Arrondir des décimaux Rapporteur et Angles Médiatrice Symétrie Axiale d'un triangle Symétrie Centrale d'un triangle Translation d'un triangle Rotation Homothétie Bissectrice Tracer droite parallèle Conversion Aires et Volumes Addition de deux relatifs Soustraction Relatifs Addition et soustraction de trois relatifs Produit Deux Relatifs Produit Trois Relatifs Quotient Relatifs Carré Entier Racine Carrée Théorème Pythagore Liste Diviseurs Décomposition Facteurs Premiers Calcul du PGCD PGCD Algorithme Euclide Test Nombre Premier Déterminer Fonction Linéaire Déterminer Fonction Affine Traceur Courbe Trigonométrie Angle Trigonométrie Longueur Périmètre d'un Cercle Aire d'un Disque Volume du Parallélépipède Rectangle Volume du cylindre Surface d'une Sphère et Volume d'une boule Volume d'une pyramide à base rectangulaire Section d'une pyramide Visualiser Section Cône en 2D Section d'un Cône Carte Mondiale Coordonnées Géographiques

Mathématiques Web c'est 2 251 056 fiches de cours et d'exercices téléchargées.